Dot product, scalability
Перейти к навигации
Перейти к поиску
Основные авторы описания: А.М.Теплов (раздел 3).
Содержание
1 Ссылки
Исследованная параллельная реализация на языке C.
2 Локальность данных и вычислений
2.1 Локальность реализации алгоритма
2.1.1 Структура обращений в память и качественная оценка локальности
2.1.2 Количественная оценка локальности
3 Масштабируемость алгоритма и его реализации
3.1 Масштабируемость алгоритма
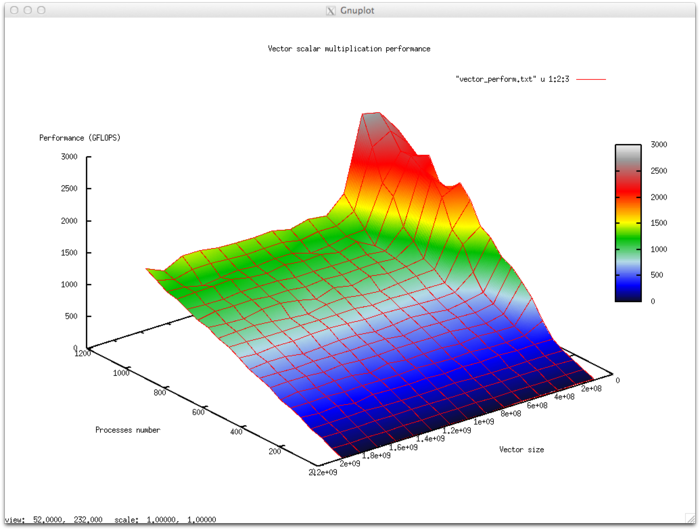
3.2 Масштабируемость реализации алгоритма
Набор изменяемых параметров запуска реализации алгоритма и границы значений параметров алгоритма:
- число процессоров [4 : 1024]
- размер вектора [134217728 : 2013265920]
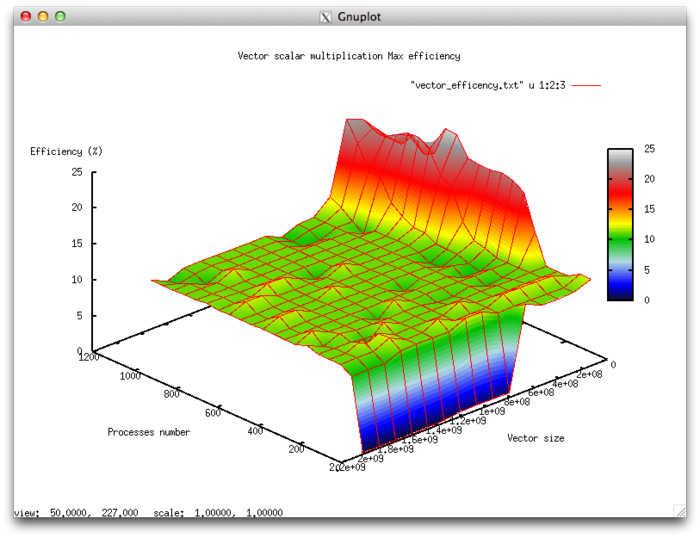
Эффективность выполнения реализации алгоритма
- Минимальная эффективность 9,54 %
- Максимальная эффективность 24,52%
Оценка масштабируемости
- По числу процессов: 0.00414 – при увеличении числа процессов эффективность увеличивается на рассмотренной области изменений параметров запуска, однако, в целом увеличение не интенсивное. Увеличение эффективности на рассмотренной области работы параллельной программы объясняется тем, что при увеличении числа процессоров декомпозиция данных в какой-то момент приводит к тому, что данные лучше укладываются в КЭШ-память. Это подтверждает проявление этого явления, но со смещением по числу процессов, и при увеличении вычислительной сложности задачи.
- По размеру задачи: -0.01385 – при увеличении размера задачи эффективность в целом уменьшается по рассматриваемой области. Это объясняется тем, что при малом размере задачи данные хорошо укладываются в КЭШ-память, что приводит к высокой эффективности работы приложения при малом размере задачи. При увеличении размера эффективность уменьшается при выходе за границы КЭШ-памяти.
- По двум направлениям: -0.000169 – при рассмотрении увеличения, как вычислительной сложности, так и числа процессов по всей рассмотренной области значений уменьшается, однако интенсивность уменьшения эффективности небольшая. В совокупности с тем фактом, что разница между максимальной и минимальной эффективностью на рассмотренной области значений параметров составляет почти 15 % говорит о том, что на поверхности присутствуют области с очень интенсивным изменением эффективности, но очень малые по площади. На остальной поверхности изменения эффективности незначительны и находятся на приблизительно одном и том же уровне.