EM Алгоритм для пуассон трехточечного распределения

Автор: Виктория Евстефеева

1 Свойства и структура алгоритмов

1.1 Общее описание алгоритма

EM-алгоритм (англ. expectation-maximization) - алгоритм итерационного типа для численного решения задачи поиска экстремума целевой функции в разнообразных задачах оптимизации. В частности, алгоритм используется в математической статистике для нахождения оценок максимального правдоподобия параметров вероятностных моделей, в случае, когда модель зависит от некоторых скрытых переменных. Каждая итерация алгоритма состоит из двух шагов. На E-шаге (expectation) вычисляется ожидаемое значение функции правдоподобия, при этом скрытые переменные рассматриваются как наблюдаемые. На M-шаге (maximization) вычисляется оценка максимального правдоподобия, таким образом увеличивается ожидаемое правдоподобие, вычисляемое на E-шаге. Затем это значение используется для E-шага на следующей итерации. Алгоритм выполняется до сходимости.

Как правило, ЕМ-алгоритм применяется для решения задач двух типов.

• К первому типу можно отнести задачи, связанные с анализом действительно неполных данных, когда некоторые статистические данные отсутствуют в силу каких-либо причин.

• Ко второму типу задач можно отнести статистические задачи, в которых функция правдоподобия имеет вид, не допускающий удобных аналитических методов исследования, но допускающий серьезные упрощения, если в задачу ввести дополнительные «ненаблюдаемые» (скрытые, латентные) переменные. Примерами прикладных задач второго типа являются задачи распознавания образов, реконструкции изображений. Математическую суть данных задач составляют задачи кластерного анализа, классификации и разделения смесей вероятностных распределений.

1.2 Математическое описание алгоритма

Задача отыскания наиболее правдопободных оценок параметров смесей вероятностных распределений является одним из самых популярных приложений ЕМ-алгоритма.

Базовым предположением в рамках данной задачи является то, что плотность наблюдаемой случайной величины [math]Χ[/math] имеет вид:

[math]f_{θ}^{X}=Σ_{i=1}^{k}p_{i}ψ_{i}(x; t_{i}),[/math]

где [math]k\geqslant 1[/math] - известное натуральное число, [math]ψ_{1}, ..., ψ_{k}[/math] - известные плотности распределения, неизвестный параметр [math]θ[/math] имеет вид [math]θ=(p_{1}, ..., p_{k}, t_{1},..., t_{k}),[/math] причем [math]p_{i}\geqslant 0,[/math] [math]i = 1, ..., k,[/math] [math] p_{1}+...+p_{k}=1,[/math] [math]t_{i},[/math] [math] i=1,...,k,[/math] - вообще говоря, многомерные параметры. Плотности [math]ψ_{1}, ..., ψ_{k}[/math] будем называть компонентами смеси, параметры [math]p_{1}, ..., p_{k}[/math] будем называть весами соответствующих компонент.

Задачей разделения смеси принято называть задачу статистического оценивания параметров [math]θ=(p_{1}, ..., p_{k}, t_{1},..., t_{k}),[/math] по известным реализациям случайно величины [math]Χ[/math]. Оценивание параметров смешанных пуассоновских моделей сводится к оцениванию смешивающего распределения. Традиционно с этой целью используется классический ЕМ алгоритм. В случае Пуассон трехточечного распределения случайной величины [math]Χ[/math] функция плотности относительно считающей меры имеет вид:

[math]f_{λ, p}^{X}=Σ_{i=1}^{k}p_{i}\frac{λ_{i}^{x}e^{-λ_{i}}}{x!},[/math]

где [math]λ[/math] - трехточечная случайная величина, то есть принимает значения [math]λ_{1}, λ_{2}, λ_{3}[/math] с вероятностями [math]p_{1}, p_{2}, p_{3}[/math] соответственно.

Итерационный ЕМ-алгоритм для оценивания неизвестных параметров [math]p_1,p_2,p_3,λ1,λ_2,λ_3[/math] определяется следующим образом. Дана выборка [math]X_1, ..., X_n[/math] независимых одинаково распределенных случайных величин таких, что

[math]P(X_i = k)=\frac{1}{k!}Σ_{j=1}^{3}p_{j}λ_{j}^{k}e^{-λ_{j}}, k = 0,1,2,...,[/math]

где [math]p_j \geqslant 0, λ_j \gt 0, j = \{1, 2, 3\}[/math] - неизвестные параметры, [math]p_1+p_2+p_3=1[/math]

Пусть [math]p^{(m)}_1, p^{(m)}_2 , p^{(m)}_3, λ_1^{(m)}, λ_2^{(m)}, λ_3^{(m)}[/math] – оценки этих параметров, полученные на [math]m[/math]-й итерации.

Таким образом ЕМ алгоритм для случая пуассон-трехточечного распределения состоит из следующих шагов:

1 шаг алгоритма - вычисление условного математического ожидания:

[math]g_{ij}^{(m)} = \frac{p_j^{(m)}e^{-λ_j^{(m)}}(λ_j^{(m)})^{X_i}}{Σ_{j=1}^{3}p_je^{-λ_j^{(m)}}(λ_j^{(m)})^{X_i}}, i=1,..., n[/math]

2 шаг алгоритма - оценивание неизвестных параметров:

[math]p_j^{(m+1)}=\frac{1}{n}Σ_{i=1}^{n}g_{ij}^{(m)}, j = \{1, 2, 3\}[/math]

[math]λ_j^{(m+1)}=\frac{Σ_{i=1}^{n}X_ig_{ij}^{(m)}}{Σ_{i=1}^{n}g_{ij}^{(m)}}, j = \{1, 2, 3\}[/math]

Функция правдоподобия для пуассон-трехточечного распределения имеет вид:

[math]L(X, λ, p)=Σ_{i=1}^{n}log(Σ_{j=1}^{3}p_{j}λ_{j}^{X_i}e^{-λ_{j}})[/math]

Для поиска более точных параметров, ЕМ алгоритм будет запускаться несколько раз с различными начальными приближениями, выбранными случайным образом.

Затем из множества полученных параметров выбираем те, чья функция правдоподобия наибольшая.

1.3 Вычислительное ядро алгоритма

Основные вычисления связаны с поиском наилучших параметров с помощью применения ЕМ алгоритма.

1.4 Макроструктура алгоритма

К исходным данным из пуассон-трехточечного распределения N раз применяется ЕМ алгоритм с различными начальными приближениями.

После этого выбираются параметры, у которых функция правдоподобия максимальна.

1.5 Схема реализации последовательного алгоритма

Здесь приведены основные моменты алгоритма.

// Плотность пуассоновского распределения
double poisson_pdf(int x, double lambda_)
{
    return pow(lambda_,x) * exp(-lambda_) / factorial(x);
}

// Функция правдоподобия для пуассон-трехточечного распределения
double likelihood(vector<int> &X, double *lambda_, double *p)
{
    double summation = 0.0;
    for (int n = 0, length_ext = X.size(); n <  length_ext; ++n)
    {
        double temp = 0.0;
        for (int k = 0; k < 3; ++k)
            temp += p[k] * poisson_pdf(X[n], lambda_[k]);
        summation += log(temp);
    }

    return summation;
}

//Вычисление начального приближения для EM алгоритма
double p[3], lambda_[3];
double minim = -100000.0;
double sum = 0.0;

for (int i = 0; i < K; ++i)
{

    p[i] = rand() % 13371337 + 1;
    sum += p[i];
}


for (int i = 0; i <  K; ++i)
    p[i] /= sum;

for (int i = 0; i < K; ++i)
{
    sum = 0.0;
    int j, l = 0;
    if (i == 0)
        j = 0;
    else
        j = int(N*p[i-1]);
    for (int q = j;  q < int(N*p[i]); ++q)
        sum += X[q];
        l += 1;
    lambda_[i] = sum/l;
}

double likely = likelihood(X, lambda_, p);
double like = minim;
if (likely > minim)
    like = likely;

// ЕМ алгоритм
while (1)
{
    //E-шаг
    for (int i = 0; i < N; ++i)
    {
        double denominator = 0.0;
        for  (int j = 0; j < K; ++j)
            denominator += p[j] * poisson_pdf(X[i], lambda_[j]);
        for (int k = 0; k < K; ++k)
            gamma[i][k] = p[k] * poisson_pdf(X[i], lambda_[k]) / denominator;
    }



    //M-шаг
    for (int k = 0; k < K; ++k)
    {
        double Nk = 0.0;
        for (int n = 0; n < N; ++n)
            Nk += gamma[n][k];

        //Вычисляем среднее
        lambda_[k] = 0.0;
        for (int n = 0; n < N; ++n)
            lambda_[k] += gamma[n][k] * X[n];
        lambda_[k] /= Nk;

        //Вычисляем коэффициенты смешивания
        p[k] = Nk / N;
    }

    double new_like = likelihood(X, lambda_, p);
    double diff = new_like - like;
    if (isnan(diff))
        break;
    if (abs(diff) < 0.0000000001)
        break;
    like = new_like;
}

1.6 Последовательная сложность алгоритма

Вычислим последовательную сложность алгоритма, основываясь на начальных данных и количестве повторов итераций запуска ЕМ алгоритма.

[math]w[/math] - количество итераций запуска ЕМ алгоритма

[math]h[/math] - количество данных

На каждой итерации ищутся параметры смеси: [math]k\cdot O(h)[/math], где [math]k[/math] - некоторая константа, которая зависит от начального приближения параметров и влияет на скорость сходимости ЕМ алгоритма, для каждой итерации может быть разной.

В итоге получаем [math]O(k \cdot w \cdot h)[/math] операций.

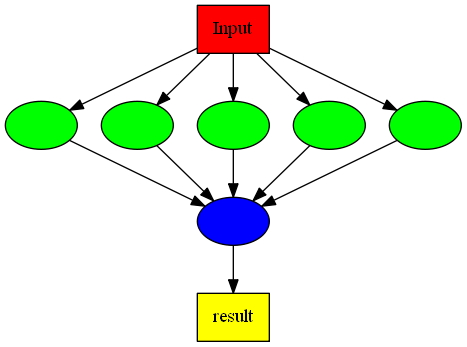
1.7 Информационный граф

Зеленые вершины - вычисление параметров ЕМ алгоритма.
Синяя вершина - вычисление оптимальных параметров на основе максимазации функции правдоподобия.

1.8 Ресурс параллелизма алгоритма

Из информационного графа видно, что вычисление параметров ЕМ алгоритма на разных итерациях происходит независимо от других, после нулевой процесс вычисляет для каждого процесса функцию правдоподобия и находит оптимальные значения параметров, максимизируя функцию правдоподобия, затем нулевой процесс записывает результат в файл. Пусть [math]N_p \geqslant 2[/math] - количество процессов. Всем процессам поручим выполнить часть итераций запуска ЕМ алгоритма (каждый процесс выполнит [math]\Big[\frac{w}{N_p - 1}\Big] [/math] итераций). Нулевому процессу поручим также принять работу и записать результат в файл.

Время работы: [math]O\Big(\frac{k \cdot w \cdot h}{N_p}\Big)[/math].

1.9 Входные и выходные данные алгоритма

На вход алгоритму подается число N - количество наблюдений, затем следует ряд из N целых чисел, предполагается, что они взяты из пуассон-трехточечного распределения. Также при запуске программы указывается сколько раз должен выполнится ЕМ алгоритм.

На выходе получаем параметры смеси, 6 вещественных чисел.

2 Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

Исследование проводилось на суперкомпьютере "Ломоносов".

Компилятор C++
Intel 13.0.1 + impi 5.1.0

Компиляция проводилась с флагом -lm.

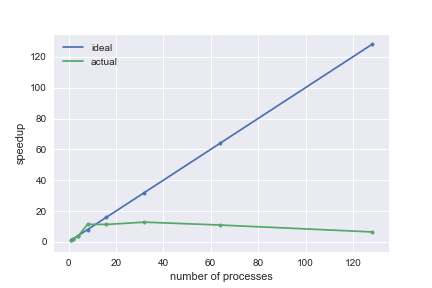
a) Количество данных - 100000, количество итераций 256.

Число процессов	Время (с)
1	40.402
2	20.654
4	10.998
8	3.541
16	3.568
32	3.153
64	3.690
128	6.233

Алгоритм перестает масштабироваться, когда время работы параллельной части алгоритма (вычисление параметров) мало по сравнению с накладными расходами MPI и временем, которое расходуется на загрузку данных.

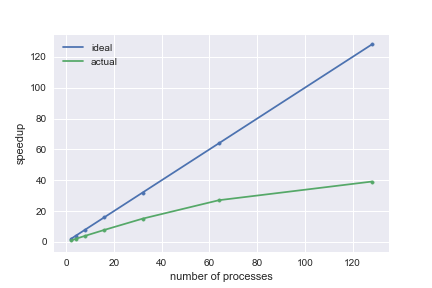
б) Количество данных - 100000, количество итераций 8192.

Число процессов	Время (с)
1	Ломоносов не досчитал, время вышло
2	647.435
4	323.948
8	162.607
16	83.009
32	42.897
64	23.928
128	16.545

Алгоритм сильно масштабируется. Время выполнения алгоритма сокращается почти в 2 раза с увеличением количества ресурсов в 2 раза.

2.7 Существующие реализации алгоритма

Подобных реализаций алгоритма не найдено.

3 Литература

↑ В.Ю. Королев "Вероятностно-статистические методы декомпозиции волатильности хаотических процессов".

↑ В. Ю. Королев, А. Ю. Корчагин, А. И. Зейфман "Теорема Пуассона для схемы испытаний Бернулли со случайной вероятностью успеха и дискретный аналог распределения Вейбулла".

↑ http://www.machinelearning.ru/wiki/index.php?title=EM-алгоритм