K-means clustering, scalability1

Основные авторы описания: Д.Бротиковская, Д.Зобнин.

1 Ссылки

Использованная параллельная реализация алгоритма k-means.

3 Масштабируемость алгоритма и его реализации

3.2 Масштабируемость реализации алгоритма

Исследование масштабируемости параллельной реализации алгоритма k-means проводилось на суперкомпьютере "Ломоносов" Суперкомпьютерного комплекса Московского университета. Алгоритм реализован на языке C с использованием средств MPI. Для исследования масштабируемости проводилось множество запусков программы с разным значением параметра (количество векторов для кластеризации), а также с различным числом процессоров. Фиксировались результаты запусков – время работы [math]t[/math] и количество произведенных итераций алгоритма [math]i[/math].

Параметры запусков для экспериментальной оценки:

• Значения количества векторов [math]n[/math]: 20'000, 30'000, 50'000, 100'000, 200'000, 300'000, 500'000, 700'000, 1'000'000, 1'500'000, 2'000'000.
• Значения количества процессоров [math]p[/math]: 1, 8, 16, 32, 64, 128, 160, 192, 224, 256, 288, 320, 352, 384, 416, 448, 480, 512.
• Значение количества кластеров [math]k[/math]: 100.
• Значение размерности векторов [math]d[/math]: 10.

Для проведения экспериментов были сгенерированы нормально распределенные псевдослучайные данные (с использованием Python библиотеки scikit-learn):

from sklearn.datasets import make_classification
X1, Y1 = make_classification(n_features=10, n_redundant=2, n_informative=8,
                             n_clusters_per_class=1, n_classes=100,
                             n_samples=2000000)

Для заданной конфигурации эксперимента ([math]n, d, p, k[/math]) и полученных результатов ([math]t, i[/math]) производительность и эффективность реализации расчитывались по формулам:

• [math]{\rm Performance} = \frac{N_{\rm k-means}^{d, n}}{t}\ \ ({\rm FLOPS}),[/math]

где [math]N_{\rm k-means}^{d, n}[/math] – точное число операций с плавающей точкой (операции с памятью, а также целочисленные операции не учитывались), вычисленное в соответствие с разделом "Последовательная сложность алгоритма";

• [math]{\rm Efficiency} = \frac{100 \cdot {\rm Performance}}{{\rm Performance}_{\rm Peak}^{p}}\ \ (\%),[/math]

где [math]{\rm Performance}_{\rm Peak}^{p}[/math] – пиковая производительность суперкомпьютера при [math]p[/math] процессорах, вычисленная согласно спецификациям Intel^® XEON^® X5670.

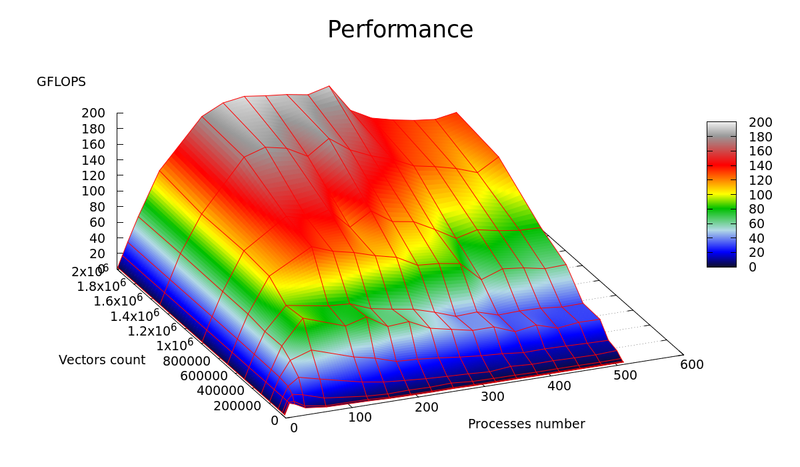
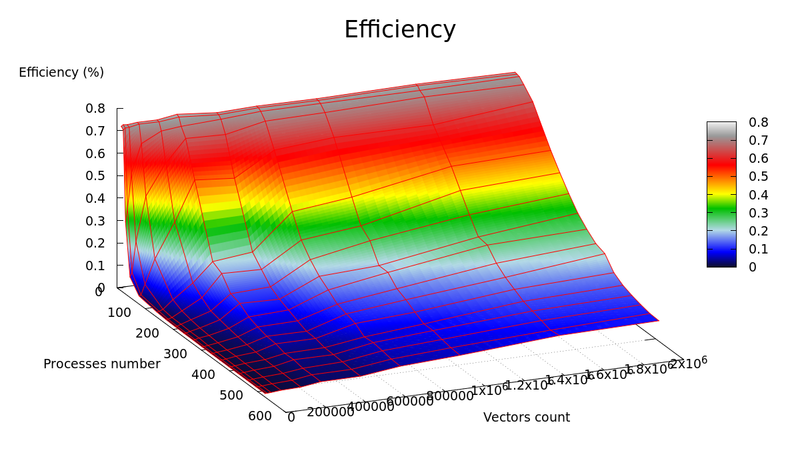
Графики зависимости производительности и эффективности параллельной реализации k-means от числа векторов для кластеризации ([math]n[/math]) и числа процессоров ([math]p[/math]) представлены на рисунках 1 и 2, соответственно.

Рис. 1. Параллельная реализация k-means. График зависимости производительности реализации алгоритма от числа векторов для кластеризации ([math]n[/math]) и числа процессоров ([math]p[/math]).

Рис. 2. Параллельная реализация k-means. График зависимости эффективности реализации алгоритма от числа векторов для кластеризации ([math]n[/math]) и числа процессоров ([math]p[/math]).

В результате экспериментальной оценки были получены следующие оценки эффективности реализации:

• Минимальное значение: 0.000409 % достигается при [math]n=20'000, p=480[/math]
• Максимальное значение: 0.741119 % достигается при [math]n=300'000, p=1[/math]

Оценки масштабируемости реализации алгоритма k-means:

• По числу процессоров: -0.002683 – эффективность убывает с ростом числа процессоров. Данный результат вызван ростом накладных расходов для обеспечения параллельного выполнения алгоритма.
• По размеру задачи: 0.002779 – эффективность растет с ростом числа векторов. Данный результат вызван тем, что при увеличении размера задачи, количество вычислений растет по сравнению с временем, затрачиваемым на пересылку данных.
• Общая оценка: -0.000058 – можно сделать вывод, что в целом эффективность реализации незначительно уменьшается с ростом размера задачи и числа процессоров.