K-means clustering, scalability4
Основные авторы описания: И.Егоров, Е.Богомазов.
Содержание
1 Ссылки
Параллельная реализация была написана самостоятельно на языке C, ссылка на реализацию. Так как на каждой итерации число действий на единицу данных не велико и данные должны быть собраны вместе при перерасчете центроидов, было решено для ускорения вычислений воспользоваться только OpenMP без использовании MPI.
2 Локальность данных и вычислений
2.1 Локальность реализации алгоритма
2.1.1 Структура обращений в память и качественная оценка локальности
2.1.2 Количественная оценка локальности
3 Масштабируемость алгоритма и его реализации
3.1 Масштабируемость алгоритма
3.2 Масштабируемость реализации алгоритма
Исследование масштабируемости данной параллельной реализации алгоритма k-средних также проводилось на суперкомпьютере "Ломоносов".
Код собирался под gcc с опцией -fopenmp. Код считался на одном процессоре, технология hyperthreading не использовалась.
Набор и границы значений изменяемых параметров запуска реализации алгоритма:
- число процессоров [1 : 16] с увеличением в 2 раза;
- размер данных [100000 : 1600000] с увеличением в 2 раза.
В результате проведённых экспериментов были получены следующие данные:
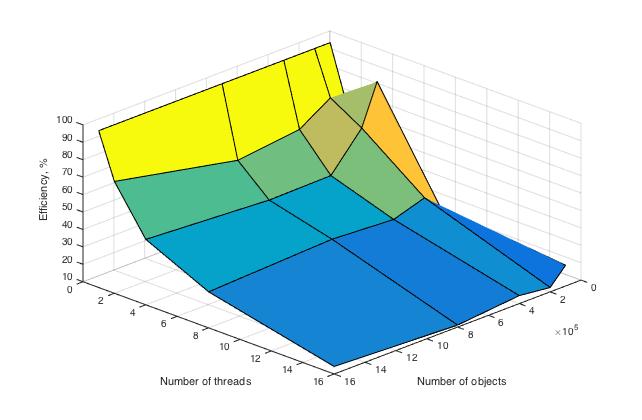
- Максимальная эффективность в точке достигается при переходе от 1 потока на 4 при минимальном размере данных, она равна 87,5%.
- Усредненная максимальная эффективность достигается при переходе с одного потока на два. Среднее время вычислений на всех рассмотренных потока снижается с 16,33 до 11.87 секунд, поэтому формально эффективность = 16.33 / 11.87 / 2 \approx 68,4\%
- Минимальная эффективность в точке достигается при переходе от 1 потока на 16 при размере данных 800000, она равна 11,1\%.
- Усредненная минимальная эффективность наблюдается при переходе с одного на максимальное рассматриваемое в эксперименте число потоков, равное 16. Время вычисления изменяется с 16,33 до 7,6 секунд, поэтому формально эффективность = 16.33 / 7.6 / 16 \approx 14,9\%
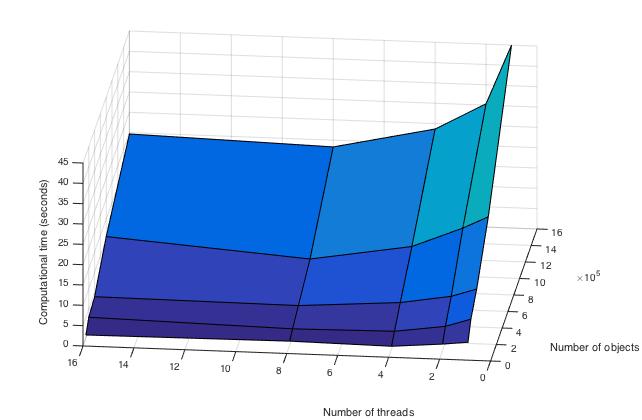
Ниже приведены графики зависимости вычислительного времени алгоритма и его эффективности от изменяемых параметров запуска — размера данных и числа процессоров:
Здесь видно, что время выполнения операций алгоритма плавно убывает по каждому из параметров, причем скорость убывания по параметру числа процессоров выше, чем в зависимости от размерности задачи.
Здесь построена эффективность перехода от последовательной реализации к параллельной. Рассчитывается она по формуле Время вычисления на 1 потоке / Время вычисления на T потоках / T, где T — это число потоков. При вычислении на 1 процессоре она равна 100 \% в силу используемой формулы, что и отражено на графике.
Проведем оценки масштабируемости:
По числу процессов — при увеличении числа процессов эффективность уменьшается на всей области рассматриваемых значений, причем темп убывания замедляется с ростом числа процессов.
По размеру задачи — при увеличении размера задачи эффективность вычислений вначале кратковременно возрастает, но затем начинает относительно равномерно убывать на всей рассматриваемой области.
По размеру задачи — при увеличении размера задачи эффективность вычислений в общем случае постепенно убывает. На малых данных она выходит на пик мощности, являющийся максимумом эффективности в исследуемых условиях, но затем возвращается к процессу убывания.