Newton's method for systems of nonlinear equations, scalability1

Основные авторы описания: К.О.Шохин, А.А.Лебедев.

1 Ссылки

Ссылка на программную реализацию метода Ньютона для решения систем нелинейных уравнений: https://github.com/ArtyLebedev/newton .

3 Масштабируемость алгоритма и его реализации

Масштабируемость алгоритма и его реализаций определяется главным образом масштабируемостью реализации алгоритма решения СЛАУ, используемого для нахождения изменения текущего решения на очередной итерации.

3.2 Масштабируемость реализации алгоритма

В исследуемой реализации для решения СЛАУ использовался метод Гаусса. Исследование проводилось для систем размером от 1024 до 4096 уравнений, с шагом 512. Исследуемая система имеет следующий вид:

[math] \left\{\begin{matrix} cos(x_1) - 1 = 0, \\ cos(x_2) - 1 = 0, \\ \vdots \\ cos(x_n) - 1 = 0. \end{matrix}\right. \qquad (2) [/math]

Данная система выбрана так как для нее известно решение, а также начальное приближение [math] x_0 = (0.87, 0.87, ..., 0.87) [/math], при котором метод Ньютона успешно сходится.

Количество ядер процессоров, на которых производились вычисления, изменялось от 16 до 128 по степеням 2. Эксперименты проводились на суперкомпьютере Ломоносов в разделе test. Исследование проводилось на узлах, обладающих следующими характеристиками:

• Количество ядер: 8 ядер архитектуры x86
• Количество памяти: 12Гб
• Количество GPU: 0

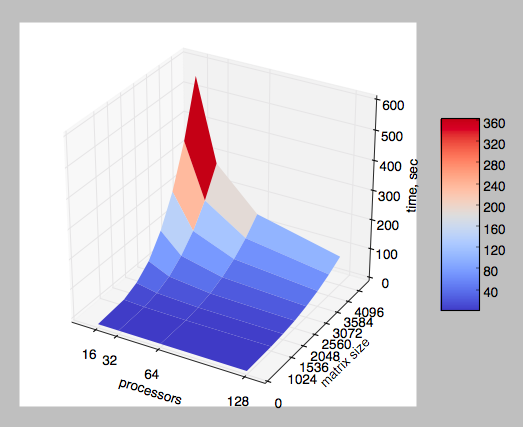
На рис. 1 показаны результаты измерений времени решения системы [math](2)[/math] в зависимости от размера системы и количества процессоров. Можно утверждать, что увеличение числа процессоров дает выигрыш во времени, однако, из-за особенностей реализации параллельного решения СЛАУ, при большом количестве узлов и большом размере системы будет осуществляться пересылка между узлами больших объемов данных и возникающие при этом задержки нивелируют выигрыш от увеличения числа процессоров. Поэтому масштабируемость исследуемой реализации весьма ограничена.

Рис.1 Время решения системы уравнений в зависимости от числа процессоров и размера задачи

Использовался компилятор g++, входящий в состав gcc version 4.4.7 20120313 (Red Hat 4.4.7-4). При компиляции указывался оптимизационный ключ -O2, использовалась библиотека Intel MPI 5.0.1.