Pairwise summation of numbers, scalability

Основные авторы описания: А.М.Теплов (раздел 3).

1 Ссылки

Исследованная параллельная реализация на языке C.

3 Масштабируемость алгоритма и его реализации

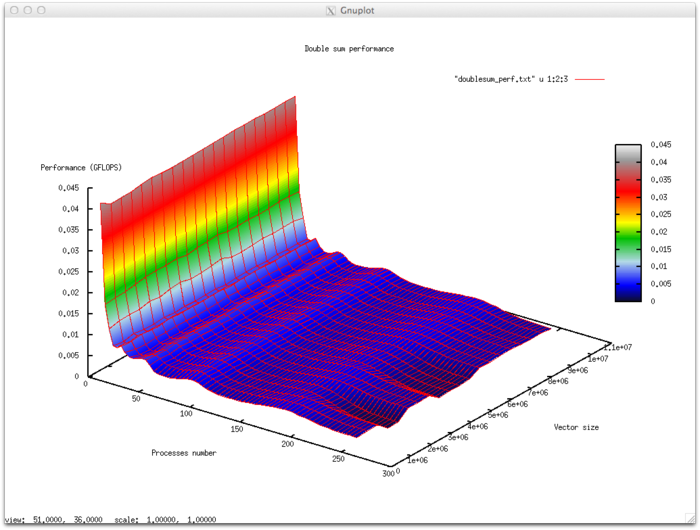
3.2 Масштабируемость реализации алгоритма

Рисунок 1. Параллельная реализация Суммирования схемой сдваивания Максимальная производительность.

Рисунок 2. Параллельная реализация суммирования схемой сдваивания Максимальная эффективность.

Набор изменяемых параметров запуска реализации алгоритма и границы значений параметров алгоритма:

• число процессоров [2 : 256]
• размер вектора [512000:10240000]

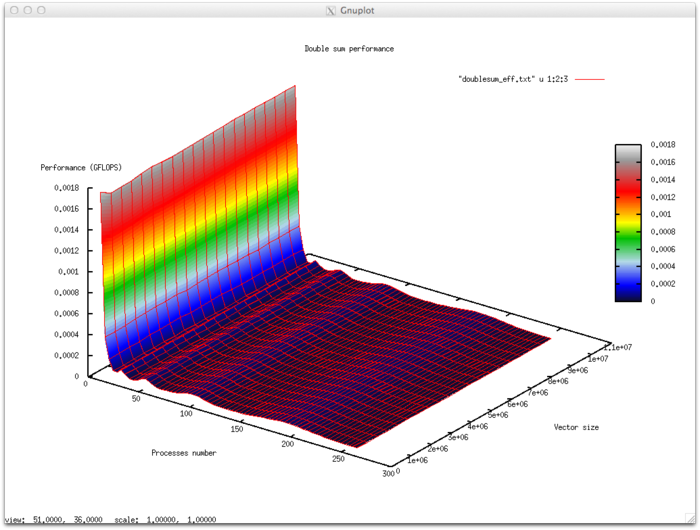
Эффективность выполнения реализации алгоритма

• Минимальная эффективность 0,00001%
• Максимальная эффективность 0,0018%

Оценка масштабируемости

• По числу процессов: -3.059e-06 – при увеличении числа процессов эффективность уменьшается на рассмотренной области изменений параметров запуска, однако, в целом уменьшение не интенсивное. Это объясняется тем, что при увеличении числа процессов доля сильно возрастают накладные расходы на организацию схемы сдваивания суммирования, однако так, как общая эффективность составляет доли процента интенсивность сильная только при переходе от работы процессов в рамках одного физического узла к использованию коммуникационной сети. В остальной области рассмотренных значений параметров запуска эффективность близка к 0 в силу того, что на каждый процесс приходится чрезвычайно малая доля вычислений. Больше полезного времени уходит на организацию работы процессов.
• По размеру задачи: 6.426e-09 – при увеличении размера задачи эффективность в целом очень незначительно увеличивается по рассматриваемой области. Это объясняется общим увеличением вычислительной сложности задачи в связи с увеличением размерности. Однако вычислительная сложность алгоритма [math](N-1)[/math]не позволяет существенно увеличить долю времени затрачиваемую на вычисления.
• По двум направлениям: -8.047e-08 – при рассмотрении увеличения, как вычислительной сложности, так и числа процессов по всей рассмотренной области значений уменьшается, однако интенсивность уменьшения эффективности небольшая. В совокупности с тем фактом, что разница между максимальной и минимальной эффективностью на рассмотренной области значений параметров несущественная говорит о том, что на поверхности присутствуют области с очень интенсивным изменением эффективности на участке 2-16 процессов, но очень малые по площади. На остальной поверхности изменения эффективности незначительны и находятся на приблизительно одном и том же уровне.