Scalability methodology
1 Проведение исследования масштабируемости реализации алгоритма.
- Выбор реализации параллельного алгоритма
- Составление списка изменяющихся параметров работы реализации (размер задачи – a, число процессов – b, размер блока – c, число процессов на узел и т.п.) – набор значений этих параметров будем называть конфигурацией запуска K=(a,b,c...)
- Выбор границ параметров, в которых будут проводиться эксперименты (максимальное и минимальное значение каждого параметра) \min(a),\max(a), \min(b),\max(b), \min(c),\max(c)...
- Для каждого изменяемого параметра необходимо выбрать набор рассматриваемых значений параметров {h_a}{h_b}{h_c}..., с которым каждый из параметров будет изменяться в серии экспериментов, лежащих в промежутке от минимального до максимального значения включительно.
- В приложении необходимо оформить фиксацию в лог-файл информации, содержащей данные о значениях изменяющихся параметров запуска (a_i,b_i,c_i...) и времени выполнения алгоритма (t_i). Результатом выполнения R будем считать совокупность параметров выполнения и времени выполнения R = (a_i,b_i,c_i...t_i). Если в одном приложении необходимо исследовать несколько частей, то можно ввести либо идентификатор исследуемой части приложения "ind" и добавить его в результат, тогда для каждого приложения результат будет состоять из двух строк, либо добавить к результату еще одно значение времени: t_{1i}, t_{2i}.
- Проведение серии экспериментов.
- Из списка выбранных параметров выбирается для каждого минимальное значение в выбранных границах (совокупность этих параметров назовем минимальной конфигурацией K_{min}= (\min(a), \min(b), \min(c),...)
- Проводится запуск приложения с минимальной конфигурацией
- Фиксируется результат выполнения (a_{min},b_{min},c_{min},...t_{min})
- Выбирается из списка параметров один параметр K_i
- Значение выбранного параметра увеличивается, подставляя следующее значение из выбранного набора значений параметра {h_{ki}}.
- Проводится запуск на новой конфигурации запуска. Лучше каждый запуск проводить несколько раз. Таким образом, можно добиться уменьшения влияния различных случайных процессов, влияющих на производительность приложения.
- Фиксируется в лог-файле новый результат выполнения
- Пока значение параметра не достигнет значения \max(K_i) повторять с шага е.
- При достижении максимума параметра Ki перейти к параметру K_{i+1}
- Значение следующего параметра выбрать из соответствующего набора значений следующим по возрастанию {h_{Ki+1}}
- Повторить для выбранного параметра шаги с d до j, до достижения максимума для этого параметра.
- Рекурсивно для каждого нового параметра необходимо проводить запуски приложения по описанной выше схеме, увеличивая значение его из выбранного набора значений и фиксировать результаты выполнения, аналогично проходя по всем значениям предыдущих параметров.
- Для проведения серии экспериментов целесообразно выстроить параметры запуска таким образом, чтобы самым последним был параметр – число процессов. В таком случае можно создать обертку для реализации алгоритма, которая будет минимизировать число запусков приложения на вычислительной системе и будет подставлять значения для других параметров, проходя рекурсивно по всем наборам значений остальных параметров запуска. Таким образом, в один физический запуск созданной обертки реализации алгоритма при фиксированном значении числа процессов необходимо уложить максимальный набор других изменяемых параметров, не влияющих на параметры физического запуска. Тогда число физических запусков обертки будет прямо пропорционально числу значений параметров влияющих на физический запуск приложения.
- Сбор результатов выполнения приложения по всем выполненным запускам в логах.
- Добавление всех собранных результатов работы приложения в базу данных следующим образом: данные из каждого файла с логами запуска приложения необходимо внести в общую таблицу базы данных. В таблице должны присутствовать поля, соответствующие каждому изменяемому параметру, поле идентификатора эксперимента, если они описаны разными строками или для каждого значения времени эксперимента должно присутствовать отдельное поле. Так же в таблицу целесообразно добавить колонки, характеризующие параметры вычислительной системы, на которой производились запуски приложения, и прочая информация о параметрах системы, которые могут отличаться при переходе к другой системе (тип и параметры процессора, параметры сети, тип и версия компилятора и т.п.). Так же целесообразно ввести поле, в котором будет содержаться информация об источнике данного результата. С помощью него можно найти из какого файла с логами работы приложения данные попали в базу, чтобы можно было отследить проблемные запуски приложения и например можно было бы отфильтровать данные этого запуска. Следует отметить, что чем более детальная информация о запуске приложения будет представлена в базе, тем более детальный анализ может быть проведен в дальнейшем.
- Проводится анализ собранной базы данных. Для этого можно строить выборки из собранных результатов экспериментов, используя аналитические функции. Основным интересующим запросом был бы запрос минимального времени выполнения каждого эксперимента по всем проведенным экспериментам, сгруппированным по числу процессоров и размеру задачи. Таким запросом мы можем найти те конфигурации, в которых производительность была максимальной. Возможно использование и других запросов к собранной базе данных. Этими запросами можно узнать динамику изменений, каких либо параметров при изменениях других параметров запуска.
- Из результатов запросов содержащих значения параметров и временя выполнения можно получить другие характеристики работы приложения, например значение производительности и эффективности. Для этого необходимо для каждого значения времени выполнения применить формулу вычисления производительности и эффективности. Для получения производительности необходимо оценить вычислительную сложность на рассматриваемом участке программы. Как правило, вычислительная сложность зависит от размера задачи. Производительность будет получена путем деления числительной сложности на время выполнения. Эффективность работы приложения можно вычислять как отношение полученной производительности к пиковой производительности. Пиковая производительность на данной конфигурации получается путем умножения числа процессов на пиковую производительность одного процессорного ядра.
- Получаем двумерную сетку значений изменения производительности и эффективности по всем рассмотренным значениям числа процессоров и рассматриваемым размерам задачи или другим параметрам. Полученные данные можно дальнейшего анализа масштабируемости параллельного приложения.
2 Выведение метрики масштабируемости
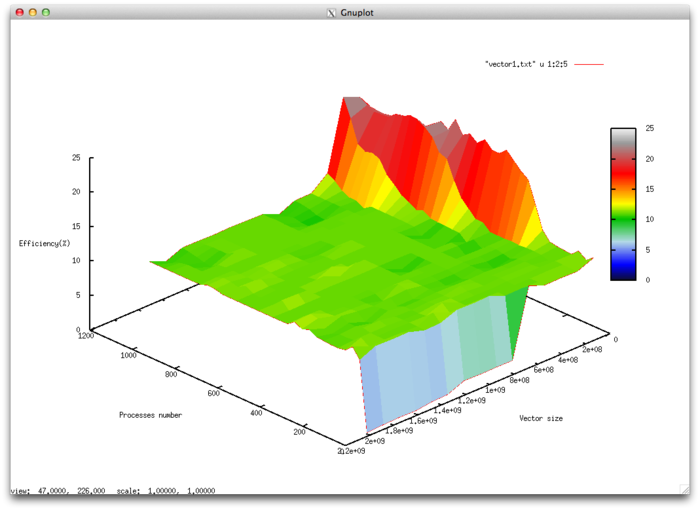
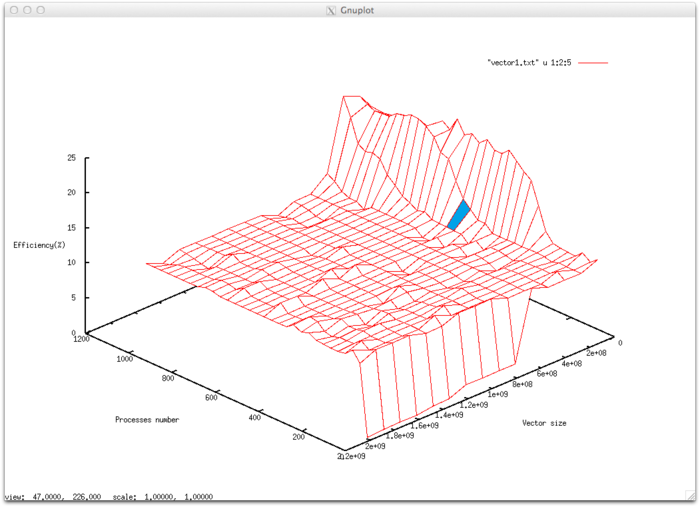
Предполагая, что о параллельном приложении собрана вся информация, характеризующая его работу на пространстве рассматриваемых значений параметров запуска, можно вывести метрику масштабируемости приложения. Рассмотрим выборку результатов экспериментов, в которой берем максимальную эффективность работы по всем проведенным запускам, сгруппированным по одинаковому числу процессов и размеру решаемой задачи. На рисунке показано, как может выглядеть трехмерное графическое представление такой выборки для приложения, реализующего скалярное произведение векторов.
Для расчета метрики рассмотрим выборку результатов экспериментов, сгруппированным по одинаковому числу процессов (P_n) и по размеру решаемой задачи (D_n), и при максимальной эффективности выполнения программы по всем проведенным запускам. Результаты эксперимента сгруппируем в группы по четыре значения эффективности из соседних значений с близкими параметрами запуска так, чтобы такими группами покрыть всю рассматриваемую область параметров. Такие группы значений будем называть элементами рассматриваемой области значений параметров. Тогда в рассматриваемой трехмерной сетке значений (по числу процессоров и размеру задачи) у каждой точки будет 3 соседних значения (для результата со значениями параметров Pn,Dn соседними будут результаты со значениями P_{n+1},D_{n}, P_{n},D_{n+1}, P_{n+1},D_{n+1}). Следовательно, три соседние точки будут у всех результатов, у которых значения параметров отличны от максимальных P_n \lt \max{P_n} и Dn\lt \max{D_n} . Но соседние результаты не будут найдены, если по каким-то причинам были пропущены какие-либо конфигурации запуска. В этом случае можно составить три соседние точки так, чтобы соседними стали те результаты, значения которых следуют за пропущенными. Таким образом, мы разобьем рассматриваемую область значений параметров на отдельные элементы (Рисунок).
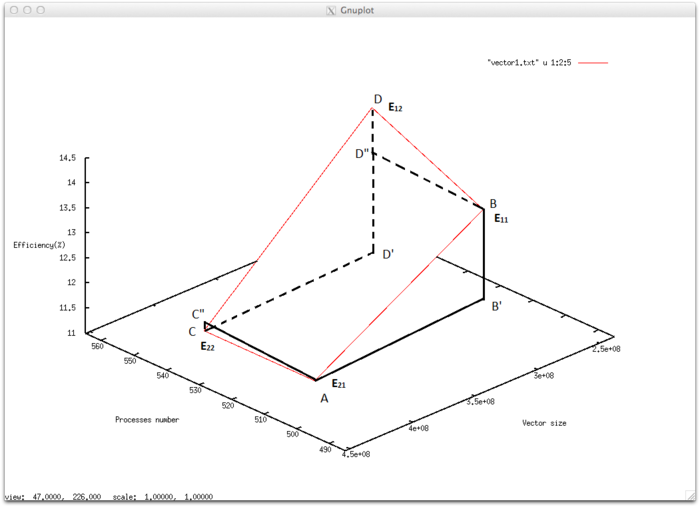
Для минимальной конфигурации запуска (P_n,D_n) можно найти ее соседние значения, так как в рассматриваемых результатах серии экспериментов изменяется число процессов и размер задачи. Далее, начиная с минимальной конфигурации, необходимо найти соседние значения для всех рассматриваемых результатов, для которых можно найти 3 соседние точки. Полученные группы результатов 4-х экспериментов с соседними значениями будем рассматривать как массив значений эффективности (E_{11} ,E_{12}, E_{21}, E_{22}).
Для каждого такого элемента этого массива вычислим приращения значения эффективности. Для этого рассмотрим изменение эффективности при увеличении значения каждого параметра. На рисунке 4 показан один из элементов рассматриваемой области параметров запуска, где отражены также проекции отрезков, соединяющих эти точки. Тогда рассматриваемым приращениям соответствуют отрезки BB', DD', CC'', DD''.
Приращением эффективности по направлению оси X (увеличение числа процессов) будем называть среднее значение приращения \Delta EP = ((E_{11} -E_{12})+(E_{21}- E_{22}))/2, если E_{11} и E_{12} – запущены с одним и тем же размером задачи, а число процессов E_{12} следует за числом процессов у E_{11}. Аналогично для E_{21} и E_{22}. Вкладом элемента рассматриваемой области значений в общую оценку масштабируемости по числу процессов будем называть величину markP=\Delta EP*(p_2-p_1)/(\max{p}-\min{p}), где p_2, p_1 – большее и меньшее значение параметра числа процессов на рассматриваемом элементе области параметров запуска.
Приращением эффективности по направлению оси Z (изменение размера задачи) будем называть среднее значение приращения \Delta ED = ((E_{11} - E_{21})+(E_{12} - E_{22}))/2, если E_{11} и E_{21}– запущены с одним и тем же числом процессов, а размер задачи E_{21} следует за размером задачи у E_{11}. Аналогично для E_{12} и E_{22}. Вкладом элемента рассматриваемой области значений в общую оценку по размеру задачи будем называть величину markD=\Delta ED*(d_2-d_1)/(\max{d}-\min{d}), где p_2, p_1 – большее и меньшее значение параметра размера задачи на рассматриваемом элементе области параметров запуска.
Приращением эффективности по всем четырем значениям будем называть среднее значение приращения \Delta EA =(\Delta EP+\Delta ED)/2, если E_{11} и E_{21}– запущены с одним и тем же числом процессов, а размер задачи E_{21} следует за размером задачи у E_{11}. Аналогично для E_{12} и E_{22}. Вкладом элемента рассматриваемой области значений в общую оценку будем называть величину markA=\Delta EA*((p_2-p_1) *(d_2-d_1))/ ((\max{p}-\min{p})* (\max{d}-\min{d})), где p_2, p_1 – большее и меньшее значение параметра размера задачи на рассматриваемом элементе области параметров запуска.
Так как мы разбили всю рассматриваемую область значений параметров на элементы, то подобные рассуждения применимы для каждого элемента. И всю область мы можем рассматривать как одномерный массив элементов рассматриваемой области.
Общей оценкой масштабируемости по числу процессов будем называть среднее значение вклада каждого элемента рассматриваемой области значений в общую оценку по числу процессов по всем элементам рассматриваемой области параметров запуска.
Mark_{Procs} =(mark_{P_1}+mark_{P_2}+...+mark_{P_N})/N
Общей оценкой масштабируемости по размеру решаемой задачи будем называть среднее значение вклада каждого элемента рассматриваемой области значений в общую оценку по размеру решаемой задачи по всем элементам рассматриваемой области параметров запуска.
Mark_{Data} =(mark_{D_1}+mark_{D_2}+...+mark_{D_N})/N
Общей оценкой масштабируемости будем называть средний размер вклада каждого элемента рассматриваемой области значений в общую оценку по всем элементам рассматриваемой области параметров запуска.
Mark_{All} =(mark_{A_1}+mark_{A_2}+...+mark_{A_N})/N
Тогда, масштабируемость параллельного приложения на рассматриваемой области параметров запуска по размеру решаемой задачи и по числу процессоров будет характеризовать метрика:
(\min{p_n},\min{d_n}, \max{p_n},\max{d_n},Mark_{Procs},Mark_{Data},Mark_{All}, \max{E_n},\min{E_n})
\min{p_n},\min{dn}, \max{pn},\max{dn} – границы значений параметров запуска рассматриваемой области
Mark_{Procs} – характеризует скорость и направление изменения на рассматриваемой области по направлению увеличения числа процессоров
Mark_{Data} – характеризует скорость и направление изменения на рассматриваемой области по направлению увеличения размера задачи
Mark_{All} – характеризует скорость и направление изменения на рассматриваемой области по направлению увеличения всех параметров запуска.
\max{E_n},\min{E_n} – границы изменения эффективности на рассмотренной области параметров запуска.
Из построения метрики вытекает несколько свойств:
общая оценка масштабируемости для рассматриваемой области, состоящей из одного элемента, будет равна оценке для этого элемента
для двух приложений с одинаковыми поверхностями изменения эффективности, но отличающимися между собой в каждом эксперименте на одну и ту же константу, оценка будет одинаковой, но отличаться будут максимальное и минимальное значения эффективности
для двух приложений, у одного из которых эффективность на всей рассматриваемой области значений является константой, а у второго эффективность меняется симметрично (до половины значений возрастает, после половины убывает с той же интенсивностью) оценка масштабируемости может совпасть и равняться 0, но будут отличаться максимальное и минимальное значения эффективности. Чтобы получить более детальную и различающуюся картину для таких приложений, целесообразно разбить рассматриваемую область на две и рассматривать их отдельно.