Uniform norm of a vector, locality
Основные авторы описания: Вад.В.Воеводин (раздел 2).
Содержание
1 Ссылки
Основной фрагмент реализации, на основе которого были получены количественные оценки, приведен здесь (функция KernelUniformNormSeqpar).
2 Локальность данных и вычислений
2.1 Локальность реализации алгоритма
2.1.1 Структура обращений в память и качественная оценка локальности
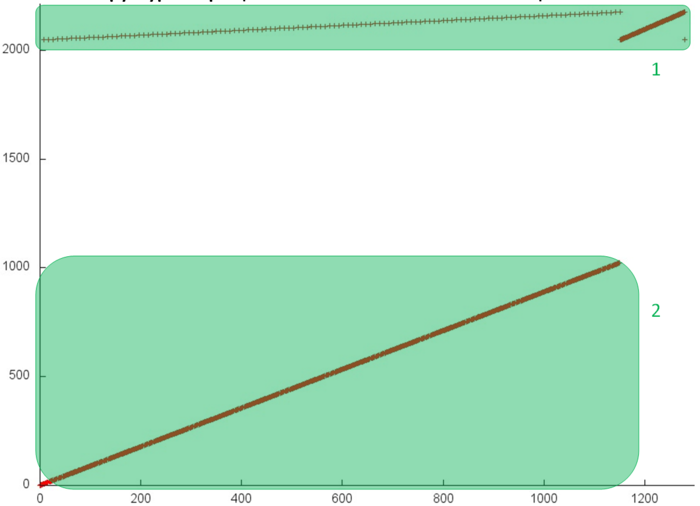
На рис.1 представлен профиль обращений в память для вычисления равномерной нормы вектора, вещественная версия. Видно, что данный профиль состоит из двух фрагментов, принадлежащих разным массивам – они выделены на рис.1 зеленым цветом. Поскольку мы рассматриваем последовательную реализацию последовательно-параллельного метода суммирования, строение профиля практически никак не зависит от выбранного количества ветвей – будет меняться только число задействованных элементов во фрагменте 1. При рассмотрении всего профиля складывается впечатление, что оба фрагмента состоят просто из последовательных переборов элементов своих массивов, однако для подтверждения этого рассмотрим каждый из них в отдельности.
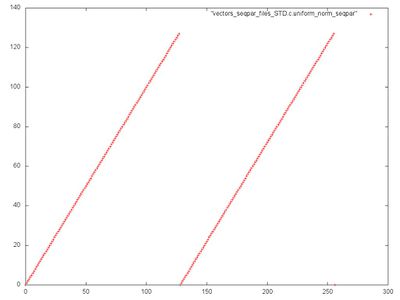
Фрагмент 1 изображен на рис.2. Видно, что он состоит из двух одинаковых последовательных переборов всех элементов массивов. Такой фрагмент обладает высокой пространственной (из-за последовательного перебора) и низкой временной (к каждому элементу обращение происходит только дважды) локальностью. Заметим, что на рис.1 эти переборы выглядят по-разному. Причина заключается в том, что первый перебор происходит одновременно с большим числом обращений ко второму массиву, что приводит к искаженному представлению. Эту особенность необходимо каждый раз учитывать при анализе профилей обращений в память.
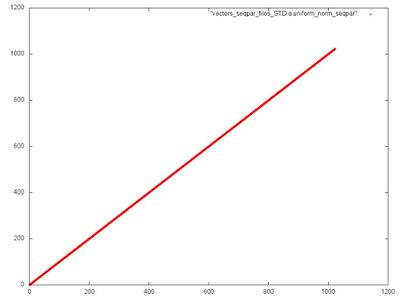
На рис.3 показан фрагмент 2. В данном случае все совсем просто – данный фрагмент состоит только из одного последовательного перебора всех элементов массива. Таким образом, временная локальность здесь достигает минимума, поскольку к каждому элементу обращение происходит только один раз.
2.1.2 Количественная оценка локальности
Условия запуска описаны здесь.
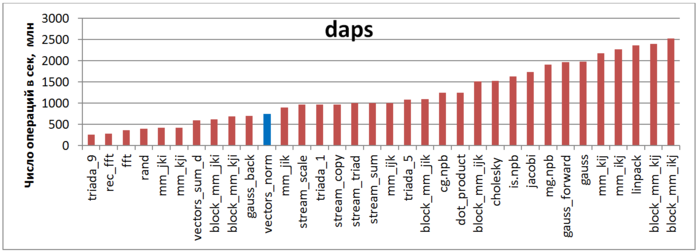
Первая оценка выполняется на основе характеристики daps, которая оценивает число выполненных обращений (чтений и записей) в память в секунду. Данная характеристика является аналогом оценки flops применительно к работе с памятью и является в большей степени оценкой производительности взаимодействия с памятью, чем оценкой локальности. Однако она служит хорошим источником информации, в том числе для сравнения с результатами по следующей характеристике cvg.
На рис.4 приведены значения daps для реализаций распространенных алгоритмов, отсортированные по возрастанию (чем больше daps, тем в общем случае выше производительность). Можно увидеть, что производительность данной программы достаточно мала, что связано с низкой временной локальностью.
Вторая характеристика – cvg – предназначена для получения более машинно-независимой оценки локальности. Она определяет, насколько часто в программе необходимо подтягивать данные в кэш-память. Соответственно, чем меньше значение cvg, тем реже это нужно делать, тем лучше локальность.
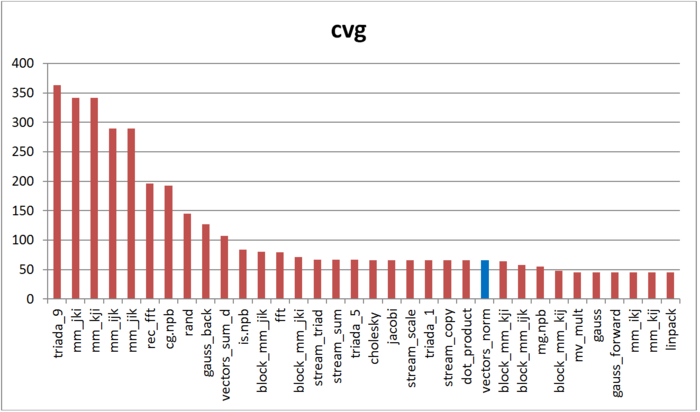
На рис.5 приведены значения cvg для того же набора реализаций, отсортированные по убыванию (чем меньше cvg, тем в общем случае выше локальность). Можно увидеть, что, согласно данной оценке, локальность рассматриваемого профиля оказалась достаточно высока. Полученная некоторая несогласованность с оценкой daps связана с высокой пространственной локальностью профиля, по всей видимости, что в большей мере повлияло на cvg, чем на daps.