Участник:Каледа Александр/Строгий алгоритм С средних (Hard C-Means)

Эта работа прошла предварительную проверку Дата последней правки страницы: 18.12.2016 Данная работа соответствует формальным критериям. Проверено Каледа Александр.

Строгий алгоритм С средних (Hard C-Means)
Последовательный алгоритм
Последовательная сложность	[math]O(nmC)[/math]
Объём входных данных	[math]nm+1[/math]
Объём выходных данных	[math](n+m)C[/math]
Параллельный алгоритм
Высота ярусно-параллельной формы	[math]O(nClog_2(nC))[/math]
Ширина ярусно-параллельной формы	[math]O(n)[/math]

Авторы описания: Каледа Александр (разделы 1.1, 1.5, 1.6, 1.7, 1.8, 1.9), Шапулин Андрей (разделы 1.2, 1.3, 1.4, 1.7, 1.10, 2.7).

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Строгий алгоритм C средних (Hard C-Means, HCM; Jang, Sun and Mizutani, 1997) один из наиболее широко используемых алгоритмов кластеризации данных. Алгоритм разбивает большие наборы векторов в многомерном пространстве по заранее заданному количеству кластеров (т.е. является управляемым).

На вход алгоритму подается набор векторов и количество кластеров. Дополнительно может задаваться пороговая величина объектной функции, при достижении которой алгоритм останавливается. После окончания работы алгоритма каждый вектор будет отнесет к определенному кластерному центру. Алгоритм, являясь итерационным, зависит от начальных значений кластерных центров, а следовательно может не сходиться к локальному минимуму.

На первом шаге алгоритма происходит инициализация кластерным центров, это можно сделать выбрав случайным образом вектора из входного набора. На следующем шаге начинается итерационный процесс, завершающийся при достижении порогового значения объектной функцией или при минимальном отличии, от значения на предыдущей итерации.

Вычисления, выполняющиеся на очередной итерации алгоритма:

1. Расчёт рядовой матрицы (сопоставление вектора соответствующему кластерному центру).
2. Расчёт объектной функции.
3. Пересчёт кластерных центров.

1.2 Математическое описание алгоритма

Исходные данные: матрица [math]U\in \mathbb{R}^{n\times m}[/math], представляющая собой набор векторов [math]\{u_i\}_{i=1}^{n}, u_i \in \mathbb{R}^m[/math]; количество кластеров [math]C \in \mathbb{N}[/math].

Вычисляемые данные: набор векторов - кластерных центров [math]\{c_i\}_{i=1}^{C}, c_i \in \mathbb{R}^m[/math]; матрица [math]M\in \mathbb{N}^{n\times C}[/math] c информацией о разбиении объектов на кластера. Элемент [math]m_{ij}=1[/math], если [math]u_j \in C_i[/math], где [math]C_i[/math] содержит все объекты [math]u[/math], принадлежащие кластеру [math]i[/math]. Остальные элементы [math]m_{ij}=0[/math].

Алгоритм:

Шаг 1. Инициализация кластерных центров [math]c_i, i = 1, 2, \dots, C.[/math] Это можно сделать выбрав случайным образом C векторов из входного набора [math]\{u_i\}_{i=1}^{n}[/math]

Шаг 2. Вычисление рядовой матрицы M.

Матрица [math]M[/math] состоит из элементов [math]M = \|m_{ik}\|[/math].

[math] m_{ik} = \begin{cases} 1, & \|u_k-c_i\|^2 \leqslant \|u_k-c_j\|^2 \;\; \text{for all } i \neq j; \;\; (i,j=1,2,\ldots,C; \; k = 1,2,\ldots,n)\\ 0, & \text{otherwise}. \end{cases} [/math]

Шаг 3. Расчет объектной функции:

[math] J = \sum\limits_{i=1}^C J_i = \sum\limits_{i=1}^C \left( \sum\limits_{k:\, u_k \in C_i} \|u_k -c_i \|^2 \right)[/math].

На этом шаге происходит остановка и выход из цикла, если полученное значение ниже пороговой величины или полученное значение не сильно отличается от значений, полученных на предыдущих циклах.

Шаг 4. Пересчет кластерных центров.

Пересчет кластерных центров выполняется в соответствии со следующим уравнением:

[math] c_i = \frac{1}{|C_i|} \sum\limits_{k:\, u_k \in C_i} u_k, [/math]

где [math]|C_i|[/math] -- количество элементов в [math]i[/math]-ом кластере.

Шаг 5. Переход на шаг 2.

Описание взято из .

1.3 Вычислительное ядро алгоритма

Вычислительное ядро алгоритма Hard C-Means можно составить из множественных (всего их [math]nC[/math]) вычислений квадратов нормы разности векторов [math]u_k[/math] и кластерных центров [math]c_i[/math]: [math]\|u_k-c_i\|^2[/math].

1.4 Макроструктура алгоритма

Как записано и в описании ядра алгоритма, основную часть метода составляют множественные ([math]Cn[/math]) вычисления квадратов норм:

[math]\|u_k-c_i\|^2[/math].

Также присутствуют данные вычислительные операции:

• Суммирование квадратов норм векторов:

[math] J = \sum\limits_{i=1}^C J_i = \sum\limits_{i=1}^C \left( \sum\limits_{k:\, u_k \in C_i} \|u_k -c_i \|^2 \right) [/math]

• Поэлементное суммирование векторов:

[math] c_i = \frac{1}{|C_i|} \sum\limits_{k:\, u_k \in C_i} u_k [/math]

1.5 Схема реализации последовательного алгоритма

Итерационный блок алгоритма можно описать на языке Python следующим образом:

for i in range(n):
    idx_min = 0
    dist_min  = ((u[i] - c[0]) ** 2).sum()

    for j in range(1, C):
        dist  = ((u[i] - c[j]) ** 2).sum()
        if dist < dist_min:
            idx_min = j
            dist_min = dist

    M[i, idx_min] = 1
    c_next[idx_min] += u[i]
    c_next_cnt[idx_min] += 1
    J += dist_min

1.6 Последовательная сложность алгоритма

Предполагаем, что предельная точность алгоритма достигаема менее, чем за [math]n[/math] итераций. Иначе использование алгоритма можно считать нерациональным. Также предположим, что размерность [math]m[/math] и количество кластерных центров [math]C[/math] существенно меньше [math]n[/math].

Операция вычисления квадрата нормы разности векторов требует выполнения [math]m-1[/math] арифметических операций сложения, [math]m[/math] операций вычитания и [math]m[/math] операций умножения.

Каждая итерация алгоритма требует выполнения:

• [math]nC[/math] операций вычисления квадрата нормы разности векторов;
• [math]nC[/math] операций сравнения квадрата нормы;
• [math]3n[/math] операций сложения;

Таким образом, на каждой итерации имеем:

• [math]mnC[/math] операций умножения;
• [math](2mC + 3)n[/math] арифметических операций сложения и вычитания;

В итоге имеем сложность последовательной реализации алгоритма [math]O(nmC)[/math].

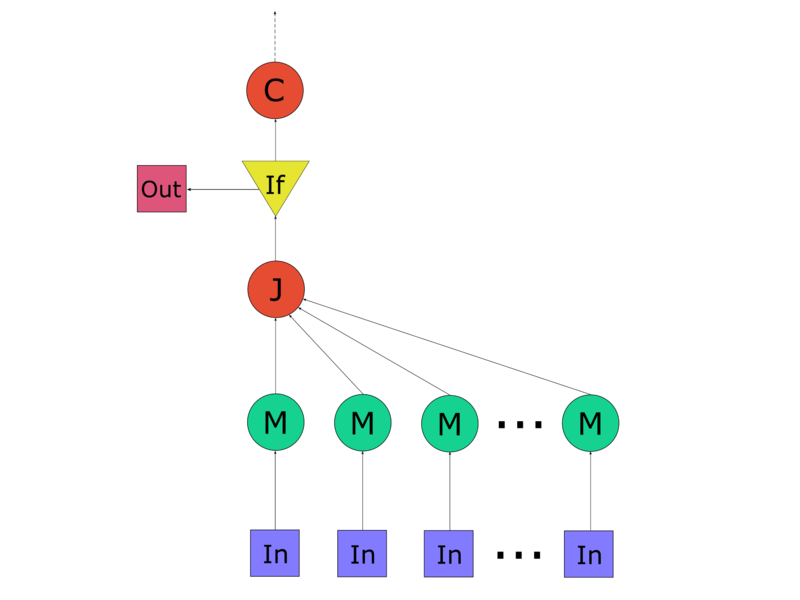
1.7 Информационный граф

Граф алгоритма состоит из 4 видов вершин:

Первая группа вершин отмечена символом M. Ей соответствует вычисление минимального расстояния до кластерных центров, а также запись единицы в соответствующий столбец матрицы, обозначающей принадлежность кластерному центру:

• независимое вычисление расстояний от заданного элемента [math]u_i[/math] до каждого из кластерных центров;
• последовательное сравнение полученных значений с целью отыскания максимума;
• операция записи 1 в соответствующий столбец матрицы принадлежности кластерным центрам;

Вторая вершина отмечена символом J, на этом этапе происходит итоговый расчёт объектной функции.

Третья вершина помечена if, на этом этапе происходит проверка условия достижения требуемой точности.

Четвертая соответствует операции пересчёта кластерных центров, она отмечена как C.

Рисунок 1. Информационный граф алгоритма. Здесь in — ввод входных данных, M — вычисление минимального расстояния до кластерных центров и проставление принадлежности соответствующему кластерному центру, J — вычисление объектной функции по результатам полученных вычислений, if — проверка условия достижения желаемой точности, C — пересчёт кластерных центров и out — вывод полученных данных.

1.8 Ресурс параллелизма алгоритма

Основной ресурс параллелизма алгоритма составляет итерационный блок. Эта последовательность итераций может быть выполнена для каждого входного вектора [math]u_i[/math] независимо. Однако, в конце выполнения каждого итерационного блока имеют место последовательные вычисления - сложение значений объектной функции, полученных независимо на каждом процессоре, а также перерасчет кластерных центров.

Число итераций алгоритма оценим как [math]O(nC)[/math]. Исходя из того, что сложность вычислительного блока [math]M[/math] равна [math]log_2(C)[/math], а сложность расчета функционала [math]J[/math] составляет [math]log_2(n)[/math], имеем, что высота итерации составляет [math]log_2(nC)[/math]. Таким образом, высота ЯПФ оценивается как [math]O(nClog_2(nC))[/math].

Ширина ЯПФ равна [math]n[/math].

Необходимо учитывать, что при небольшом объеме входной выборки, параллельная реализация алгоритма может лишь понизить производительность. В первую очередь это связано с пересылкой данных для вычисления итоговых значений объектной функции и кластерных центров.

1.9 Входные и выходные данные алгоритма

Входные данные: матрица [math]U\in \mathbb{R}^{n\times m}[/math], представляющая собой набор векторов [math]\{u_i\}_{i=1}^{n}, u_i \in \mathbb{R}^m[/math]; количество кластеров [math]C \in \mathbb{N}[/math].

Объём входных данных: [math]nm+1[/math].

Выходные данные: набор векторов - кластерных центров [math]\{c_i\}_{i=1}^{C}, c_i \in \mathbb{R}^m[/math]; матрица [math]M\in \mathbb{N}^{n\times C}[/math] c информацией о разбиении объектов на кластера. Элемент [math]m_{ij}=1[/math], если [math]u_j \in C_i[/math], где [math]C_i[/math] содержит все объекты [math]u[/math], принадлежащие кластеру [math]i[/math]. Остальные элементы [math]m_{ij}=0[/math].

Объём выходных данных: [math](n+m)C[/math].

1.10 Свойства алгоритма

Достоинства:

• лёгкость реализации;
• вычислительная простота;
• может служить для кластеризации больших наборов числовых данных;

Недостатки:

• задание количества кластеров;
• отсутствие гарантии в нахождении оптимального решения;

Соотношение последовательной и параллельной сложности алгоритма: линейное.

Вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных равна константе.

Алгоритм является недетерминированным, т.к. он является итерационным с выходом по точности, а также использует датчик случайных чисел для инициализации кластерных центров.

2 Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

Проведём исследование масштабируемости параллельной реализации строгого алгоритма C средних согласно методике.

Исследование проводилось на 1U сервере со следующими характеристиками:

• 2 x Intel® Xeon® Processor E5-2697 v2, всего 24 физических ядра (48 логических ядра при включенном Hyper-Threading);
• 128GB RAM;

2.4.1 Масштабируемость реализации алгоритма

Сборка осуществлялась со следующими параметрами:

• GCC-4.8.4;
• OpenMP-3.1;
• аргументы компилятора: -std=c++11 -O3;

Набор и границы значений изменяемых параметров запуска реализации алгоритма:

• число логических ядер [1 : 48] с шагом 2;
• размерность пространства [3 : 50] c шагом 3;
• число векторов 100 000 000;
• число кластерных центров 30;

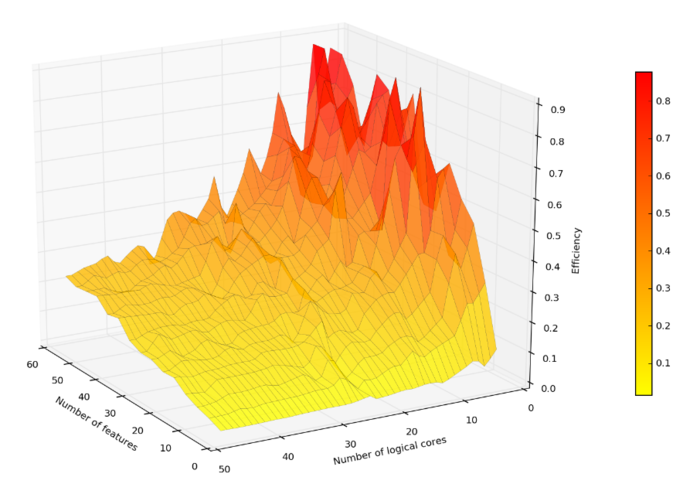
В результате проведённых экспериментов был получен следующий диапазон эффективности реализации алгоритма (отношение реальной производительности программы к пиковым показателям работы вычислительной системы):

• минимальная эффективность реализации 0.014;
• максимальная эффективность реализации 0.9;

На следующих рисунках приведены графики производительности и эффективности выбранной реализации HCM в зависимости от изменяемых параметров запуска.

Рисунок 2. Параллельная реализация алгоритма. Изменение производительности в зависимости от числа процессоров и размерности векторов.

Рисунок 3. Параллельная реализация алгоритма. Изменение эффективности в зависимости от числа процессоров и размерности векторов.

2.4.2 Реализация на языке C++

Исследованная параллельная реализация на языке C++

2.7 Существующие реализации алгоритма

• Последовательная реализация алгоритма на MatLab
• Последовательная реализация алгоритма на С++