Участник:Timokhinivan/Быстрое преобразование Фурье

Эта работа прошла предварительную проверку Дата последней правки страницы: 11.11.2016 Данная работа соответствует формальным критериям. Проверено IgorS.

Быстрое преобразование Фурье
Последовательный алгоритм
Последовательная сложность	[math]O(N \log N)[/math]
Объём входных данных	[math]N[/math]
Объём выходных данных	[math]N[/math]
Параллельный алгоритм
Высота ярусно-параллельной формы	[math]O(\log N)[/math]
Ширина ярусно-параллельной формы	[math]O(N)[/math]

Автор описания: Тимохин И.В., ВМК МГУ.

1 Свойства и структура алгоритмов

1.1 Общее описание алгоритма

Преобразование Фурье переводит сигнал в его спектр и обратно, и широко применяется в самых различных областях вычислительной математики — собственно спектральный анализ, сжатие данных, вычисление свёрток и т.д. В связи с этим, особый интерес представляют быстрые алгоритмы для вычисления этого преобразование. На сегодняшний день, наилучшие из них имеют сложность [math]O(n \log n)[/math].

1.2 Математическое описание алгоритма

Преобразование Фурье задаётся следующей формулой:

[math] Y_k = \sum_{l = 0}^{N-1} X_l \epsilon^{kl}_N,\qquad k = \overline{0,N-1} [/math]

где [math]\epsilon_N = e^{-\frac{2i\pi}{N}}[/math] — первообразный корень из 1 степени [math]N[/math].

Таким образом, преобразование Фурье является линейным и задаётся матрицей [math]F = \left\{ \epsilon^{kl}_N \right\}_{k\,l = 0}^{N-1}[/math].

1.2.1 Многомерное преобразование Фурье

Естественным обобщением описанного одномерного преобразования Фурье является многомерный вариант:

[math] Y(l_1,\ldots,l_d) = \sum_{k_1 = 0}^{N_1-1} \cdots \sum_{k_d = 0}^{N_d-1} X(k_1,\ldots,k_d) \prod_{j=1}^{d} \epsilon_{N_j}^{l_j k_j} [/math]

Многомерное преобразование Фурье эквивалентно последовательному выполнению одномерных преобразований по каждому измерению; при использовании для этого рекурсивного алгоритма, общая сложность вычислений также составляет [math]O(N\log N)[/math], [math]N = \prod_{j=1}^d N_j[/math].

1.2.2 Сведение к (почти) двумерному преобразованию (алгоритм Кули-Тьюки)

Если [math]N[/math] — составное, т.е. [math]N = mn[/math], то возможно существенно сократить вычислительные расходы за счёт сведения к двумерному преобразованию Фурье. А именно, положим [math]X(l_1, l_2) = X_{l_1 n + l_2}[/math], [math] Y(k_1, k_2) = Y_{k_1 m + k_2}[/math], где [math]l_1, k_2 = \overline{0, m-1}[/math], [math]l_2, k_1 = \overline{0, n-1}[/math].

В этом случае

[math] \begin{align} Y(k_1, k_2) &=& \sum_{l_2=0}^{n-1} (\epsilon^{k_2 l_2}_N \hat{X}(k_2, l_2)) \epsilon^{k_1 l_2}_n \\ \hat{X}(k_2, l_2) &=& \sum_{l_1=0}^{m-1} X(l_1, l_2) \epsilon^{k_2 l_1}_m \end{align} [/math]

Это даёт следующий алгоритм вычисления преобразования:

1. Записываем исходный вектор в матрицу [math]m\times n[/math] по строкам.
2. Применяем к каждому столбцу преобразование Фурье.
3. Умножаем элемент в позиции [math](i,j)[/math] на [math]\epsilon^{ij}_N[/math].
4. Применяем к каждой строке преобразование Фурье.
5. Результат записан в получившейся матрице по столбцам.

Данный алгоритм уже даёт существенный выигрыш по сравнению с обычным умножением матрицы на вектор: [math] O(m^2 n + n^2 m) [/math] против [math]O(m^2 n^2)[/math]. Однако наилучших результатов можно добиться, если применять этот алгоритм рекурсивно на этапах 2 и 4.

Так, если [math]N = \prod_{i=1}^{K} p_i[/math], то целесообразно на каждом уровне рекурсии «отщеплять» одно [math]p_i[/math]. В этом случае задача сводится к вычислению [math] \prod_{i\neq j} p_i [/math] преобразований Фурье порядка [math]p_j[/math] для всех [math]j[/math]. При небольших [math]p_i[/math] (например, 2), это можно проделывать «в лоб».

1.2.3 Преобразование Фурье с большим простым порядком (алгоритм Радера)

В случае, если порядок преобразования простой, но ещё слишком большой, чтобы вычислять его непосредственно, задача усложняется. Алгоритм в этом случае такой:

1. [math] Y_0 = \sum_{l=0}^{N-1} X_l[/math] вычисляется непосредственно.
2. Любым способом вычисляется [math]g[/math] — первообразный корень мультипликативной группы поля [math]\mathbb{Z}_{N}[/math].
3. [math] Y_{g^{N-p} \bmod N} = X_0 + \sum_{q=0}^{N-2} X_{g^q \bmod N} \epsilon_N^{g^{q-p}\bmod N} [/math].

Последнее выражение представляет собой свёртку и вычисляется с помощью всё того же преобразования Фурье. В принципе, это можно проделывать непосредственно, поскольку порядок свёртки [math]N - 1[/math] уже составной (по меньшей мере чётный), но, поскольку свёртка, в отличие от самого преобразования Фурье, допускает увеличение порядка, имеет смысл воспользоваться этим и выбрать порядок с небольшими простыми множителями.

Таким образом, поскольку при правильной реализации подавляющее большинство рекурсивных вызовов будет использовать алгоритм Кули-Тьюки, в дальнейшем будет рассматриваться именно он.

1.3 Вычислительное ядро алгоритма

На каждом уровне рекурсии наиболее дорогостоящими этапами являются рекурсивные вызовы преобразования Фурье: они требуют в сумме [math]O(mn (\log m + \log n))[/math] операций против [math]O(mn)[/math] для умножения на поправочные коэффициенты (шаг 3).

То же верно и для алгоритма в целом в случае [math]N = \prod_{i=1}^{K} p_i[/math]; а именно, суммарно наибольшие вычислительные затраты связаны с вычислением преобразований Фурье порядка [math]p_i[/math].

1.4 Макроструктура алгоритма

Фактически, макроструктура алгоритма уже описана в разделе математического описания. На каждом уровне рекурсии, алгоритм состоит из

1. [math]n[/math] рекурсивных вызовов алгоритма.
2. Умножение всех элементов рабочего вектора на поправочные коэффициенты.
3. Ещё [math]m[/math] рекурсивных вызовов.

1.5 Схема реализации последовательного алгоритма

Псевдокод (для метода Кули-Тьюки):

fft(X, N)
begin
  (m, n) = factor(N)

  if (n == 1) // Предполагается, что n <= m
    direct_fft(X, N) // Через умножение на матрицу

  // 1
  transpose(X, m, n) //Транспонирует X как матрицу m x n, хранящуюся по строкам
   
  // 2
  do i = 0, n - 1
    fft(X(i * m : (i + 1) * m - 1), m)

  // 3
  do i = 0, n - 1
    do j = 0, m - 1
      X(i * m + j) *= eps(i * j, N)

  // 4
  transpose(X, n, m)

  // 5
  do j = 0, m - 1
    fft(X(j * n : (j + 1) * n - 1), n)

  // 6
  transpose(X, m, n)
end

Здесь eps может как вычислять соответствующие коэффициенты, так и брать их из заранее заготовленной таблицы. Последний способ требует увеличения затрат по памяти, но позволяет существенно сэкономить на вычислениях, а потому является предпочтительным.

Кроме того, шаги 3 и 4 можно переставлять произвольным образом (с очевидными изменениями в шаге 3).

Особо следует отметить, что если порядок элементов в выходном массиве не важен, шаг 6 можно пропустить.

Так, например, если преобразование Фурье используется для вычисления свёртки векторов, то конкретный порядок элементов в их образах Фурье совершенно не важен, лишь бы он был одинаков для обоих векторов. В этом случае в прямом преобразовании можно опустить шаг 6, а в обратном — 1.

Если необходимо учитывать случай большого простого [math]N[/math] (что может и не требоваться, в зависимости от задачи), то в первом условном операторе следует дополнительно проверить величину [math]N[/math] и, если [math]N[/math] большое, переключиться на алгоритм Радера.

1.6 Последовательная сложность алгоритма

Непосредственно из описания алгоритма получаем, что если сложность вычисления преобразования Фурье обозначить [math]f_N[/math], то [math]f_{mn} = n f_{m} + m f_{n} + mn[/math].

Если [math]N = \prod_{i=1}^K p_i[/math], и на каждом шаге «отщеплять» от него одно [math]p_i[/math], а преобразование Фурье для [math]p_i[/math] вычислять «в лоб», то общее количество операций составит [math]O\left(N\sum_{i=1}^K p_i\right)[/math].

В частности, если [math]p_i \leq P[/math], то [math]K \leq \log_P N[/math] и для сложности получаем [math]O(NP\log_P N)[/math]. Полагая [math]P[/math] фиксированным, получаем заявленную сложность [math]O(N \log N)[/math].

1.7 Информационный граф

Рисунок 1. Информационный граф алгоритма Кули-Тьюки для [math]N = 15[/math]. Исходные данные обозначены фиолетовым, результат — красным. Преобразования Фурье для [math]m = 5[/math] и [math]n = 3[/math] представлены как «чёрные ящики». Умножение на поворотные коэффициенты представлено оранжевыми узлами.

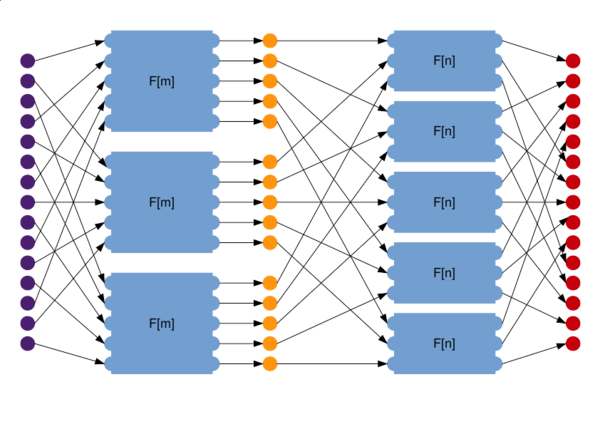
Каждый уровень рекурсивного вызова состоит из трёх этапов: рекурсивный вызов по столбцам, умножение на поправочные коэффициенты и рекурсивного вызова по строкам. Таким образом для высоты ЯПФ имеем

[math] h(mn) = 1 + h(m) + h(n) [/math]

Для «элементарных» БПФ высота ЯПФ будет та же, что и для умножения матрицы на вектор.

Таким образом, с учётом разложения [math]N[/math], [math]h(N) = O\left(\sum_{i=1}^K p_i\right) = O(P \log_P N) = O(\log N)[/math].

1.8 Ресурс параллелизма алгоритма

Поскольку все рекурсивные вызовы преобразования Фурье на каждом из этапов совершенно независимы, кажется естественным распределить их по доступным вычислительным узлам. Умножение на поворотные коэффициенты при этом и вовсе выполняется независимо на каждом элементе рабочего вектора, и может быть беспрепятственно присоединёно к любому из этапов.

При этом, в отличие от традиционной реализации, в которой на каждом этапе один из множителей берётся малым, при параллельной реализации целесообразно взять и [math]m[/math] и [math]n[/math] по возможности близкими к кратным доступному количеству вычислительных узлов, поскольку в этом случае возможно равномерно распределить работу между ними и реализовать весь алгоритм всего с одной внутренней пересылкой.

1.9 Входные и выходные данные алгоритма

В общем случае на входе и на выходе имеются комплексные векторы порядка [math]N[/math]. Однако в частных случаях, возможны более компактные представления для параметров и результатов.

Для описания этих случаев нам понадобится матрица

[math] Q = \begin{bmatrix} 1 & & & & & \\ & & & & & 1 \\ & & & & 1 & \\ & & & \cdots & & \\ & & 1 & & & \\ & 1 & & & & \end{bmatrix} [/math]

1. Если [math]X[/math] — вещественный, то [math]Y = Q\bar{Y}[/math].
2. Если [math]X[/math] — чисто мнимый, то [math]Y = -Q\bar{Y}[/math].
3. Если [math]X = Q\bar{X}[/math], то [math]Y[/math] — вещественный.
4. Если [math]X = -Q\bar{X}[/math], то [math]Y[/math] — чисто мнимый.

В каждом случае, [math]X[/math] и [math]Y[/math] требуют для своего хранения в два раза меньше памяти, чем в общем случае.

Таким образом, при наличии дополнительной информации о входном векторе, возможно сократить объём памяти используемый для хранения входных и выходных данных.

1.10 Свойства алгоритма

Обозначая матрицу преобразования [math]F[/math], имеем:

1. [math]F = F^T[/math]
2. [math]F^{-1} = \tfrac{1}{N} F^*[/math]
3. [math]F^* = QF [/math]

Свойство 2 представляет особый интерес, поскольку позволяет вычислять обратное преобразование Фурье по тем же алгоритмам, что и прямое, поскольку [math]F^*[/math] представляет собой матрицу того же вида, что и [math]F[/math], но с [math]\bar{\epsilon}[/math] вместо [math]\epsilon[/math]. В сущности, свойство 3 позволяет свести задачу к исходной непосредственно, но ценой дополнительных пересылок.

Кроме того, из второго свойства следует

[math] \|F x\|_2 = \sqrt{N} \|x\|_2 [/math]

что свидетельствует о численной устойчивости алгоритма.

2 Программная реализация алгоритма

2.1 Особенности реализации последовательного алгоритма

При реализации последовательной версии алгоритма (а равно и параллельной, поскольку на определённом уровне рекурсии алгоритм всё равно будет выполняться на каждом узле независимо) стоит иметь ввиду несколько вещей:

2.1.1 Поворотные коэффициенты

Как уже упоминалось, поворотные коэффициенты имеет смысл вычислить заранее и хранить в специальном массиве. Отдельное внимание при этом стоит обратить на передачу этого массива в рекурсивные вызовы.

В самом деле, поскольку [math]\epsilon^{l}_{n} = \epsilon^{lm}_{mn} = \epsilon^{lm}_{N}[/math], все необходимые рекурсивному вызову значения поворотных коэффициентов уже имеются в используемом в текущем вызове массиве, а потому его достаточно подготовить один раз на весь алгоритм.

2.1.2 Нерекурсивный случай

На нижнем уровне рекурсии преобразование Фурье вычисляется путём умножения на матрицу. Поскольку этот алгоритм, вообще говоря, более пригоден для векторизации, чем рекурсивная реализация, имеет смысл не разбивать [math]N[/math] на совсем мелкие множители ([math]p_i \equiv 2[/math] в алгоритме Кули-Тьюки) а останавливаться на преобразованиях несколько большего порядка; конкретный уровень зависит от конкретной реализации и архитектуры и должен быть установлен экспериментально.

2.1.3 Пересылки

Теоретически, возможна реализация алгоритма совсем без пересылок, если предполагать, что алгоритм оперирует «разреженным» вектором, элементы которого расположены с некоторым шагом по памяти. Однако ценой такой экономии будет существенно худшая локальность обращений к данным в рекурсивных вызовах. По-видимому, выбор нужно опять-таки осуществлять экспериментально.

Эти соображения в равной степени относятся как к рабочему массиву, так и к массиву поворотных коэффициентов.

2.1.4 Предварительные вычисления

Многие используемые в алгоритме данные зависят только от порядка преобразования — массив поворотных коэффициентов, факторизация [math]N[/math], [math]g[/math] в алгоритме Радера, конкретная задаваемая им перестановка и оптимальный порядок свёртки там же. Вычисление некоторых из них сопоставимо по сложности со всем остальным алгоритмом. Имея это ввиду, если планируется вычисление нескольких преобразований Фурье одного порядка, имеет смысл подготовить все эти данные заранее.

2.1.5 Численная устойчивость

Поскольку все преобразования в алгоритме являются, с точностью до константы [math]\leq \sqrt{N}[/math], унитарными, катастрофического роста ошибок округления не предвидится, а потому все вычисления возможно проводить с целевой точностью.

2.2 Локальность данных и вычислений

Рисунок 2. Профиль обращений в память простого алгоритма Кули-Тьюки с [math]p = (2, 2, 3, 5, 2)[/math]. Сверху вниз: вспомогательная память для прямого умножения матрицы на вектор, память для хранения поворотных коэффициентов, рабочий вектор. Реализация не использует транспонирования векторов в явном виде.

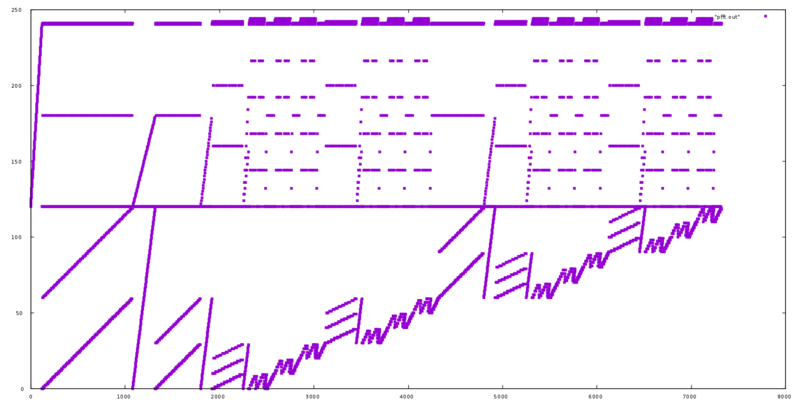
Как видно, алгоритм в целом обладает невысокой локальностью, что связано с его структурой (множество рекурсивных шагов, каждый из которых охватывает существенную часть рабочего вектора) и организацией доступа к поворотным коэффициентам. Некоторого улучшения локальности можно добиться, если транспонировать рабочую «матрицу» в памяти, но это либо требует дополнительной памяти, либо, если транспонировать «на месте», существенно усложняет алгоритм.

2.3 Возможные способы и особенности параллельной реализации алгоритма

В случае составного [math]N[/math] с достаточно большими делителями, наиболее очевидным и простым вариантом является распределение по процессорам рекурсивных вызовов алгоритма Кули-Тьюки. В этом случае на весь алгоритм приходится только три пересылки, но зато они проходят по схеме «все-со-всеми» (транспонирование матрицы) и не могут выполняться параллельно с вычислениями.

Отдельно заметим, что, как уже упоминалось, первой либо последней группы пересылок можно избежать, если порядок элементов результата не важен.

Если [math]N[/math] простое либо один из множителей в [math]N = mn[/math] всегда мал, ситуация усложняется. В этом случае придётся применять алгоритм Радера на межпроцессорном уровне, что связано с более сложной схемой пересылок и большим их количеством (т.к. приходится осуществлять преобразование Фурье дважды: прямое и обратное).

В связи с этим, некоторые существующие реализации (например, Intel® MKL) просто не поддерживают этот случай. Впрочем, некоторые реализации не поддерживают большие простые делители вовсе.

2.7 Существующие реализации алгоритма

Алгоритм быстрого преобразования Фурье относится к базовым алгоритмам вычислительной математики, а потому его реализации существуют во многих библиотеках. Перечислим некоторые из них:

• Intel® Math Kernel Library — содержит в том числе и версию для распределённых систем. Имеет интерфейсы для C, C++ и Fortran.
• FFTW — содержит распределённую реализацию начиная с версии 3.3. Имеет интерфейсы для C и Fortran.
• GNU Scientific Library — имеет интерфейс для C.
• cuFFT — реализация алгоритма для GPU от NVIDIA.
• clFFT — реализация алгоритма на OpenCL для CPU и GPU. Поддерживает только [math]N = 2^p 3^q 5^r 7^s[/math]
• IBM® Engineering and Scientific Subroutine Library — для процессоров IBM® POWER™, имеет интерфейсы для C, C++ и Fortran, существует версия для многопроцессорных систем.