Участник:ADovganich/Нечеткий алгоритм С средних: различия между версиями
ASA (обсуждение | вклад) |
Protsenko (обсуждение | вклад) |
||
| Строка 174: | Строка 174: | ||
== Масштабируемость алгоритма и его реализации == | == Масштабируемость алгоритма и его реализации == | ||
| − | Исследование | + | Проведём исследование масштабируемости параллельной реализации разложения Холецкого согласно [[Scalability methodology|методике]]. Исследование проводилось на суперкомпьютере "Ломоносов"<ref name="Lom">Воеводин Вл., Жуматий С., Соболев С., Антонов А., Брызгалов П., Никитенко Д., Стефанов К., Воеводин Вад. Практика суперкомпьютера «Ломоносов» // Открытые системы, 2012, N 7, С. 36-39.</ref> [http://parallel.ru/cluster Суперкомпьютерного комплекса Московского университета]. |
| + | |||
| + | абор и границы значений изменяемых [[Глоссарий#Параметры запуска|параметров запуска]] реализации алгоритма: | ||
| + | |||
| + | * число процессоров [1 : 120]; | ||
| + | * размер входных данных [1 : 15 000] верторок размерности 4. | ||
| + | При количестве кластеров 100. | ||
[[file: Эффективность.jpg |thumb|center|700px|Изменение эффективности.]] | [[file: Эффективность.jpg |thumb|center|700px|Изменение эффективности.]] | ||
Версия 23:57, 18 ноября 2016
| Нечеткий алгоритм C средних | |
| Последовательный алгоритм | |
| Последовательная сложность | [math]O(C*C*K*I)[/math]., где [math]I[/math] - количество итераций |
| Объём входных данных | [math]K*N[/math], [количество векторов * размерность] |
| Объём выходных данных | [math]C*K[/math], [элементы матрицы принадлежности] |
| Параллельный алгоритм | |
| Высота ярусно-параллельной формы | [math]3I[/math] |
| Ширина ярусно-параллельной формы | [math]C*C*K[/math] |
Авторы : Мария Проценко (1.5-1.8, 2.7), Андрей Довганич (1.1-1.4, 1.9, 1.10)
Содержание
- 1 Свойства и структура алгоритмов
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритмов
1.1 Общее описание алгоритма
Нечеткий алгоритм C-средних (fuzzy C-means) позволяет разбить имеющееся множество векторов (точек) мощностью [math]K[/math] на заданное число нечетких множеств. Предназначен для кластеризации больших наборов данных. Основным достоинством алгоритма является нечеткость при определении объекта в кластер. Благодаря этому становится возможным определить объекты, которые находятся на границе, в кластеры. Из основного достоинства следует и главный недостаток - неопределенность с объектами, удаленными от центров всех кластеров. В остальном ему присущи стандартные проблемы подобного класса алгоритмов: вычислительная сложность, необходимость задания количества кластеров[1].
Алгоритм был разработан J.C. Dunn в 1973 г.[2], усовершенствован J.C. Bezdek в 1981 г.[3].
На вход алгоритм получает некоторое множество входных векторов и случайную матрицу их принадлежности к каждому из кластеров. На выходе с заданной точностью получаем матрицу принадлежности.
В общем виде алгоритм можно записать следующим образом:
- Инициализировать матрицу принадлежности;
- Вычислить центры кластеров;
- Вычислить значение решающей функции. Если значение ниже некоторого порогового или его улучшение по сравнению с предыдущей итерацией меньше определенной величины, то остановить вычисления;
- Иначе вычислить новые значения матрицы принадлежности;
- Перейти к шагу 2
1.2 Математическое описание алгоритма
Рассмотрим матрицу [math] M = m_{ik} \in[0,1],\; i = 1, ..., c, \; k = 1, ..., K [/math]. [math]m_{i,k}[/math] - вероятность принадлежности объекта [math]k[/math] к кластеру [math]i[/math]; [math]c[/math] - количество кластеров, [math]K[/math] - количество векторов. При этом элементы матрицы удовлетворяют следующим условиям:
- сумма элементов в каждом столбце равна [math]1[/math];
- сумма всех элементов матрицы равно [math]K[/math];
Назовем [math] M [/math] матрицей принадлежности.
Пусть [math]c_{i} (i = 1,2,...c)[/math] - центры кластеров. Тогда рассмотрим функцию
[math] \begin{align} J(M, c_{1}, c_{2},...c_{c}) = \sum_{i = 1}^{c}{J_{i}} = \sum_{i = 1}^{c}\sum_{k = 1}^{K}{m_{ik}^q}d_{ik}^2 ~(1) \end{align} [/math]
где [math] d_{ik} = \left\Vert{u_{k}-c_{i}}\right\| [/math] - Евклидово расстояние между центром кластера и объектом, [math] 1 \le q \le \infty [/math] - экспоненциальный весовой коэффициент, характеризующий нечеткость. Будем минимизировать значение функции [math] J [/math]. Для этого вычислим центры кластеров по формуле [math] ~(2) [/math].
[math]c_{i} = {{\sum_{k = 1}^{K}{m_{ik}^q} * u_{k}} \over {\sum_{k = 1}^{K}{m_{ik}^q}}}~(2)[/math]
где [math]m_{ik}[/math] — коэффициент принадлежности [math]u_{k}[/math] вектора к кластеру [math]c_{i}[/math]
и новые значения матрицы [math] M [/math] по формуле [math] ~(3) [/math]
[math]m_{ik} = {1 \over \sum_{j = 1}^{c}{({{d_{ik}} \over {d_{jk}}})}^{2 \over q-1}} ~(3)[/math]
[math] ~(2) [/math] и [math] ~(3) [/math]являются необходимым условиями достижения минимума функцией [math] J [/math]. Таким образом эти два условия дают нам итерационный процесс.
Полностью алгоритм можно записать следующим образом:
- Инициализировать матрицу принадлежности [math] M [/math] случайными значениями от 0 до 1;
- Вычислить центры кластеров [math]c_{i} (i = 1,2,...c)[/math] используя формулу [math]~(2)[/math];
- Вычислить значение решающей функции по формуле [math]~(1)[/math]. Если значение [math] J \lt \varepsilon,~\varepsilon \gt 0[/math] или [math] |J_{i} - J_{i-1}| \lt \delta,~\delta \gt 0 [/math], то остановить вычисления;
- Иначе вычислить новые значения матрицы М по формуле [math]~(3)[/math];
- Перейти к шагу 2
1.3 Вычислительное ядро алгоритма
Вычислительным ядром алгоритма являются формулы: [math] (1) [/math], [math] (2) [/math], [math] (3) [/math]. В них производится вычисление новых центров кластеров, значения решающей функции и пересчет элементов матрицы принадлежности.
1.4 Макроструктура алгоритма
Макроструктура алгоритма состоит из следующих шагов:
- Инициализация матрицы [math] M [/math] случайными значениями от 0 до 1;
- Вычисление центров кластеров;
- Вычисление значения решающей функции(если оно удовлетворяет условиям останова - завершение вычислений);
- Вычисление новых элементов матрицы принадлежности;
- Переход к шагу 2;
1.5 Схема реализации последовательного алгоритма
Пример реализации алгоритма на языке С++. Сначала вычислим центры кластеров, потом вычислим решающую функцию, с ее помощью определим необходимость продолжать алгоритм, и при необходимости вычислим новые значения матрицы M.
float ** m;
int *c;
int number_clusters, number_items;
m = gen_random_clusters();//заполним матрицу m случайными значениями от 0 до 1
while (true)
{
//вычисление центров кластеров
for (int i=0; i<number_clusters; i++)
{
numerator==denumerator=0;
for (int k=0; k<number_items; k++)
{
numerator+=pow(m[i, k], q)*u[k];//u[k]-вектор
denumerator+=pow(m[i, k], q);
}
c[i]= numerator / denumerator;//центры кластеров
}
j=0;//вычисление решающей функции
for (int i=0; i<number_clusters; i++)
for (int k=0; k<number_items; k++)
j+=pow(m[i, k], q)*pow(dist(c[i], x[k],2);//dist-вычисляет расстояние между заданными векторами
if ((abs(j-last_j)<delta) || (j<eps)) break;//проверка на необходимость завернешения алгоритма
last_j=j;
//обновление матрицы m
for (int i=0; i<number_clusters; i++)
for (int k=0; k<number_items; k++)
{
m[i,k]=0
for(int j=0; j<number_clusters; j++)
m[i,k]+=pow(dist(c[i], x[k])/dist(c[j], x[k]),2/(q-1));
m[i,k]=1/m[i,k];
}
}
1.6 Последовательная сложность алгоритма
Каждая итерация включает в себя
- Вычисление центров кластеров [math]O(C*K)[/math]
- Вычисление решающей функции [math]O(C*K)[/math]
- Обновлене матрицы [math]M[/math] [math]O(C*C*K)[/math]
Общая сложность каждой итерации [math]O(C*C*K)[/math].
Сложность всего алгоритма будет зависеть от числа итераций, которое зависит от
- Выбора начального приближения
- Выбора условий останова
Окончательно, сложность алгоритма будет равна произведению количества итераций на их сложность
1.7 Информационный граф
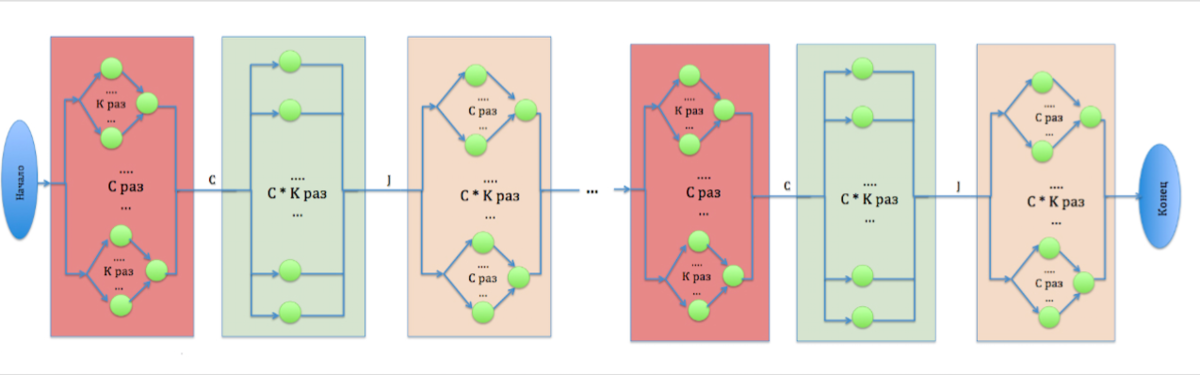
Первый ярус состоит из [math]C[/math] параллельных операций, каждая их которых в свою очередь состоит из [math]K[/math] параллельных операций, и одной, которая выполняется с использованием результата предыдущих. Результатом работы этого яруса являются значения центров кластеров , которые будут использоваться на следующем ярусе.
Второй ярус содержит в себе [math]C*K[/math] параллельных операций. Результатом его работы является значение решающей функции [math]J[/math]. Её значение определяет необходимость завершения алгоритма.
Третий ярус включает [math]C*K[/math] параллельных операций, каждая из которых состоит из [math]C[/math] параллельных операций, и одной, которая выполняется с использованием результата предыдущих.
1.8 Ресурс параллелизма алгоритма
На каждом шаге алгоритма необходимо вычислять сумму элементов массивов. Сложность ее вычисления на первом шаге (вычисление центров кластеров) при параллельной реализации составляет [math]O(\log_{2} C)[/math]. Для каждого элемента из набора входных данных([math] K [/math]), но здесь возможен независимый расчет(координатный параллелизм). На втором шаге(вычисление решающей функции) сложность будет [math]O(\log_{2} {C*K})[/math], потому что здесь необходимо сложение всех элементов. На третьем шаге имеем сложность [math]O(\log_{2} C^2)[/math]. Итого суммарная сложность итерации: [math]O(\log_{2} {C*K} + \log_{2} C^3)[/math]. Воспользовавшись свойствами логарифма произведения получаем: [math]O(\log_{2} {K} + \log_{2} C^4)[/math].
Скошенного параллелизма в алгоритме нет.
1.9 Входные и выходные данные алгоритма
Входные данные:
- [math]u_{k} ~k = 1, ..., K[/math] - набор входных векторов размерности [math] N [/math];
- [math]C[/math] - количество кластеров;
- [math]q[/math] - экспоненциальный весовой коэффициент, характеризующий нечеткость;
- [math]\varepsilon \gt 0, ~\delta \gt 0[/math] - коэффициенты, описывающие точность алгоритма.
Объем входных данных: [math] K*N [/math]
Выходные данные:
- [math] M [/math] - матрица принадлежности.
Объем выходных данных: [math] C*K [/math]
1.10 Свойства алгоритма
- Соотношение последовательной и параллельной сложности алгоритма: [math]C*C*K \over {\log_{2} {K} + \log_{2} C^4}[/math]. Соответственно при распараллеливании наибольший прирост в производительности мы получим при разбиении большого набора данных на большее число кластеров;
- Вычислительная мощность: [math]{{C^2*K} \over {C*K}} = C[/math]. Получается, что на чем большее количество кластеров мы разбиваем набор данных, тем менее затратным становится перемещение данных;
- Алгоритм не является устойчивым, как и другие подобные алгоритмы этого класса(например k-means). Очень многое зависит как от входных данных, так и от изначальных параметров приближения(заполнения матрицы принадлежности => исходных центров кластеров);
- Не является детерминированным. Так же очень многое зависит как от входных данных, так и от изначальных параметров приближения(заполнения матрицы принадлежности => исходных центров кластеров);
- Алгоритм не сбалансирован - доминирует операция умножения. Параллельные ветви алгоритма сбалансированы;
- Степень исхода вершины информационного графа - 2.
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
Проведём исследование масштабируемости параллельной реализации разложения Холецкого согласно методике. Исследование проводилось на суперкомпьютере "Ломоносов"[4] Суперкомпьютерного комплекса Московского университета.
абор и границы значений изменяемых параметров запуска реализации алгоритма:
- число процессоров [1 : 120];
- размер входных данных [1 : 15 000] верторок размерности 4.
При количестве кластеров 100.
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
Можно найти следующие реализации алгоритма
- Для MATLAB http://www.mathworks.com/help/fuzzy/fcm.html
- В PostgreSQL http://num-meth.srcc.msu.ru/zhurnal/tom_2012/v13r207.html
Так же готовые реализации алгоритма и его описание можно найти на сайтах
- https://habrahabr.ru/post/208496/
- http://pythonhosted.org/scikit-fuzzy/auto_examples/plot_cmeans.html
- http://www.codeproject.com/Articles/91675/Computer-Vision-Applications-with-C-Fuzzy-C-means
- https://github.com/gyaikhom/fcm
3 Литература
- ↑ Нейский И.М. Классификация и сравнение методов кластеризации
- ↑ Dunn, J. C. (1973-01-01). "A Fuzzy Relative of the ISODATA Process and Its Use in Detecting Compact Well-Separated Clusters". Journal of Cybernetics. 3 (3): 32–57. doi:10.1080/01969727308546046. ISSN 0022-0280.
- ↑ Bezdek, James C. (1981). Pattern Recognition with Fuzzy Objective Function Algorithms. ISBN 0-306-40671-3.
- ↑ Воеводин Вл., Жуматий С., Соболев С., Антонов А., Брызгалов П., Никитенко Д., Стефанов К., Воеводин Вад. Практика суперкомпьютера «Ломоносов» // Открытые системы, 2012, N 7, С. 36-39.