Участник:Vvnikolaev/Решето Эратосфена: различия между версиями
| (не показано 16 промежуточных версий этого же участника) | |||
| Строка 1: | Строка 1: | ||
| + | Автор статьи: Николаев Владимир | ||
| + | |||
= Свойства и структура алгоритмов = | = Свойства и структура алгоритмов = | ||
== Общее описание алгоритма == | == Общее описание алгоритма == | ||
| − | '''Решето́ Эратосфе́на''' — алгоритм нахождения всех простых чисел до некоторого целого числа <math>n</math>. Приписывается древнегреческому математику Эратосфену Киренскому (откуда и название). Алгоритм проходит список всех чисел от <math>2</math> до <math>n</math> и на каждом шаге убирает часть | + | '''Решето́ Эратосфе́на''' — алгоритм нахождения всех простых чисел до некоторого целого числа <math>n</math>. Приписывается древнегреческому математику Эратосфену Киренскому (откуда и название). Алгоритм проходит список всех чисел от <math>2</math> до <math>n</math> и на каждом шаге убирает часть из них, не являющихся простыми. Таким образом происходит фильтрация («решето» в названии). |
== Математическое описание алгоритма == | == Математическое описание алгоритма == | ||
| Строка 8: | Строка 10: | ||
# Выписываются подряд все натуральные числа от <math>2</math> до <math>n</math> | # Выписываются подряд все натуральные числа от <math>2</math> до <math>n</math> | ||
| − | # | + | # Берется <math>p = 2</math> |
| − | # Зачеркиваются числа от <math> | + | # Зачеркиваются числа от <math>p^2</math> до <math>n</math> с шагом <math>p</math> (то есть все числа от <math>2</math> до <math>n</math>, кратные <math>p</math>, кроме него самого) |
# Ищется первое не зачеркнутое число в списке, превышающие <math>p</math>, и это значение присваивается переменной <math>p</math> | # Ищется первое не зачеркнутое число в списке, превышающие <math>p</math>, и это значение присваивается переменной <math>p</math> | ||
# Повторяются шаги 3 и 4 пока возможно | # Повторяются шаги 3 и 4 пока возможно | ||
| − | + | Соответственно алгоритм заканчивает свою работу при <math>p^2 > n</math>. | |
== Вычислительное ядро алгоритма == | == Вычислительное ядро алгоритма == | ||
| − | Основное время работы приходится на шаг №3 алгоритма. Можно показать, что сложность составляет <math>O(nlog(log(n)))</math>. | + | Основное время работы приходится на шаг №3 алгоритма. Можно показать, что сложность алгоритма составляет <math>O(nlog(log(n)))</math>. |
== Макроструктура алгоритма == | == Макроструктура алгоритма == | ||
Алгоритм можно разбить на 2 части: | Алгоритм можно разбить на 2 части: | ||
| − | # Первая часть — создается булев массив длины n | + | # Первая часть — создается и заполняется единицами булев массив длины <math>n</math> |
# Вторая часть — последовательно рассматривается каждое, еще не помеченное число, и с помощью него производится фильтрация бо́льших чисел | # Вторая часть — последовательно рассматривается каждое, еще не помеченное число, и с помощью него производится фильтрация бо́льших чисел | ||
| Строка 61: | Строка 63: | ||
== Масштабируемость алгоритма и его реализации == | == Масштабируемость алгоритма и его реализации == | ||
| − | + | Исследование проводилось на суперкомпьютере "Ломоносов"<ref name="Lom">Воеводин Вл., Жуматий С., Соболев С., Антонов А., Брызгалов П., Никитенко Д., Стефанов К., Воеводин Вад. Практика суперкомпьютера «Ломоносов» // Открытые системы, 2012, N 7, С. 36-39.</ref> [http://parallel.ru/cluster Суперкомпьютерного комплекса Московского университета]. | |
| + | |||
| + | График сильной масштабируемости: | ||
| + | |||
| + | [[File:Strong_scaling_sieve.png]] | ||
| + | |||
| + | Число, до которого нужно искать простые числа, <math> n = 10^7 </math>. По графику видно, что распараллеливание дает выигрыш в скорости выполнения, но с увеличением числа используемых ядер, этот выигрыш все меньше. Это связано с лишними накладными расходами. | ||
| − | |||
| − | + | График слабой масштабируемости: | |
| − | + | [[File:Weak_scaling_sieve.png]] | |
| − | + | ||
| + | При одном процессе, число <math> n \approx 5000000 </math>. Видно, что при фиксированном отношении сложности задачи к числу процессов, время решения задачи растет. Это связано с тем, что при распараллеливании появляются дополнительные накладные расходы, а так же с тем, что задача распараллеливается не полностью. При увеличении сложности задачи в <math> 64 </math> раза (и одновременно числа процессов, потому что производилось исследование слабой масштабируемости), время выполнения увеличилось в <math> 5 </math> раз. | ||
== Динамические характеристики и эффективность реализации алгоритма == | == Динамические характеристики и эффективность реализации алгоритма == | ||
| Строка 76: | Строка 84: | ||
== Существующие реализации алгоритма == | == Существующие реализации алгоритма == | ||
| − | + | Однопоточные реализации с различными улучшениями: | |
| + | # Однопоточная реализация: http://e-maxx.ru/algo/eratosthenes_sieve | ||
| + | # Однопоточная реализация, работающая за сублинейное время: http://e-maxx.ru/algo/prime_sieve_linear | ||
| + | |||
| + | Многопоточные реализации: | ||
| + | # https://github.com/keyfunda/primes-parallel-sieve | ||
| + | # https://github.com/Heliosmaster/BSPEratosthenes | ||
| + | # https://github.com/marius92mc/sieve-of-eratosthenes-with-MPI | ||
= Литература = | = Литература = | ||
Текущая версия на 21:01, 30 ноября 2016
Автор статьи: Николаев Владимир
Содержание
- 1 Свойства и структура алгоритмов
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритмов
1.1 Общее описание алгоритма
Решето́ Эратосфе́на — алгоритм нахождения всех простых чисел до некоторого целого числа [math]n[/math]. Приписывается древнегреческому математику Эратосфену Киренскому (откуда и название). Алгоритм проходит список всех чисел от [math]2[/math] до [math]n[/math] и на каждом шаге убирает часть из них, не являющихся простыми. Таким образом происходит фильтрация («решето» в названии).
1.2 Математическое описание алгоритма
Пусть требуется найти все простые числа от [math]2[/math] до [math]n[/math]. Алгоритм состоит из следующих шагов:
- Выписываются подряд все натуральные числа от [math]2[/math] до [math]n[/math]
- Берется [math]p = 2[/math]
- Зачеркиваются числа от [math]p^2[/math] до [math]n[/math] с шагом [math]p[/math] (то есть все числа от [math]2[/math] до [math]n[/math], кратные [math]p[/math], кроме него самого)
- Ищется первое не зачеркнутое число в списке, превышающие [math]p[/math], и это значение присваивается переменной [math]p[/math]
- Повторяются шаги 3 и 4 пока возможно
Соответственно алгоритм заканчивает свою работу при [math]p^2 \gt n[/math].
1.3 Вычислительное ядро алгоритма
Основное время работы приходится на шаг №3 алгоритма. Можно показать, что сложность алгоритма составляет [math]O(nlog(log(n)))[/math].
1.4 Макроструктура алгоритма
Алгоритм можно разбить на 2 части:
- Первая часть — создается и заполняется единицами булев массив длины [math]n[/math]
- Вторая часть — последовательно рассматривается каждое, еще не помеченное число, и с помощью него производится фильтрация бо́льших чисел
1.5 Схема реализации последовательного алгоритма
Псевдокод вычислительного ядра алгоритма:
Вход: натуральное число n
Пусть A — булев массив, индексируемый числами от 2 до n, изначально заполненный значениями true.
для i := 2, 3, 4, ..., пока i2 ≤ n:
если A[i] = true:
для j := i2, i2 + i, i2 + 2i, ..., пока j ≤ n:
A[j] := false
Выход: числа i, для которых A[i] = true.
1.6 Последовательная сложность алгоритма
Сложность алгоритма складывается из двух составляющих. Первое — выписывание всех чисел от [math]2[/math] до [math]n[/math]. Это, очевидно, делается за [math]O(n)[/math]. Вторая составляющая — повторение шагов 3 и 4 — вычислительное ядро алгоритма. Сложность этой части составляет [math]O(nlog(log(n)))[/math]. Строгое доказательство этого факта можно найти в книге Hardy и Wright «An Introduction to the Theory of Numbers»[1].
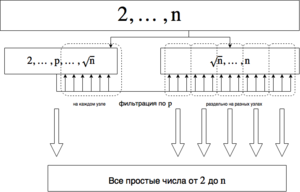
1.7 Информационный граф
Информационный граф рассматриваемого алгоритма:
1.8 Ресурс параллелизма алгоритма
Вычислительное ядро алгоритма можно распараллелить, но не полностью. Разобьем все натуральные числа [math]\{2, \dots, n\}[/math] на 2 множества — [math]\{2, \dots, \sqrt n\}[/math] и [math]\{\sqrt n + 1\dots, n\}[/math]. Поиск простых чисел на первом множестве распараллелить нельзя, а на втором — можно (различия заключаются в том, что числа из второго множества не будут проверяться в качестве делителей — они все больше [math] \sqrt n [/math]). Поэтому проверка на простоту для первого множества будет выполняться на каждом потоке, а второе можно разбить на [math]p[/math] частей ([math]p[/math] — количество процессов) и проверять каждую часть на простоту отдельно. Так как первая часть при больших [math]n[/math] значительно меньше второй, то можно предположить, что параллельное выполнение даст хороший прирост к скорости.
1.9 Входные и выходные данные алгоритма
Входные данные алгоритма — одно число [math]n[/math], до которого нужно найти все простые числа. На выходе алгоритм выдает либо булев массив длины [math]n[/math], отражающий для каждого натурального числа, является ли оно простым, либо список простых чисел от [math]2[/math] до [math]n[/math] (что конкретно — зависит от реализации и не имеет особого значения).
1.10 Свойства алгоритма
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
Исследование проводилось на суперкомпьютере "Ломоносов"[2] Суперкомпьютерного комплекса Московского университета.
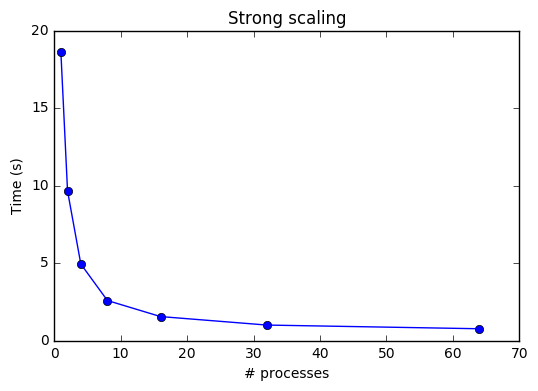
График сильной масштабируемости:
Число, до которого нужно искать простые числа, [math] n = 10^7 [/math]. По графику видно, что распараллеливание дает выигрыш в скорости выполнения, но с увеличением числа используемых ядер, этот выигрыш все меньше. Это связано с лишними накладными расходами.
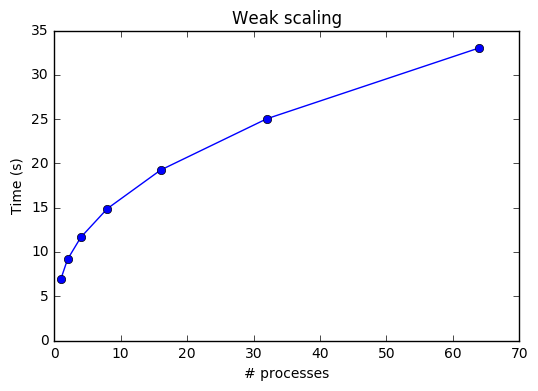
График слабой масштабируемости:
При одном процессе, число [math] n \approx 5000000 [/math]. Видно, что при фиксированном отношении сложности задачи к числу процессов, время решения задачи растет. Это связано с тем, что при распараллеливании появляются дополнительные накладные расходы, а так же с тем, что задача распараллеливается не полностью. При увеличении сложности задачи в [math] 64 [/math] раза (и одновременно числа процессов, потому что производилось исследование слабой масштабируемости), время выполнения увеличилось в [math] 5 [/math] раз.
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
Однопоточные реализации с различными улучшениями:
- Однопоточная реализация: http://e-maxx.ru/algo/eratosthenes_sieve
- Однопоточная реализация, работающая за сублинейное время: http://e-maxx.ru/algo/prime_sieve_linear
Многопоточные реализации:
- https://github.com/keyfunda/primes-parallel-sieve
- https://github.com/Heliosmaster/BSPEratosthenes
- https://github.com/marius92mc/sieve-of-eratosthenes-with-MPI
3 Литература
- ↑ Hardy and Wright "An Introduction to the Theory of Numbers, p. 349
- ↑ Воеводин Вл., Жуматий С., Соболев С., Антонов А., Брызгалов П., Никитенко Д., Стефанов К., Воеводин Вад. Практика суперкомпьютера «Ломоносов» // Открытые системы, 2012, N 7, С. 36-39.