Участник:Иванов Даниил/Алгоритм устойчивой кластеризации с иcпользованием связей: различия между версиями
Перейти к навигации
Перейти к поиску
Divanov (обсуждение | вклад) |
Divanov (обсуждение | вклад) |
||
| Строка 2: | Строка 2: | ||
| name = Алгоритм устойчивой кластеризации с иcпользованием связей | | name = Алгоритм устойчивой кластеризации с иcпользованием связей | ||
| serial_complexity = <math> O(n^2 + n m_m m_a + n^2 \log{} n)</math> | | serial_complexity = <math> O(n^2 + n m_m m_a + n^2 \log{} n)</math> | ||
| − | | input_data = <math>n \times m</math> | + | | input_data = <math>n \times m</math> (n объектов с m аттрибутами каждый) |
| − | | output_data = <math>n</math> | + | | output_data = <math>n</math> (метки кластеров для каждого объекта) |
}} | }} | ||
= ЧАСТЬ. Свойства и структура алгоритмов = | = ЧАСТЬ. Свойства и структура алгоритмов = | ||
Версия 12:07, 4 декабря 2016
| Алгоритм устойчивой кластеризации с иcпользованием связей | |
| Последовательный алгоритм | |
| Последовательная сложность | [math] O(n^2 + n m_m m_a + n^2 \log{} n)[/math] |
| Объём входных данных | [math]n \times m[/math] (n объектов с m аттрибутами каждый) |
| Объём выходных данных | [math]n[/math] (метки кластеров для каждого объекта) |
Содержание
- 1 ЧАСТЬ. Свойства и структура алгоритмов
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 ЧАСТЬ. Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 ЧАСТЬ. Свойства и структура алгоритмов
1.1 Общее описание алгоритма
- Алгоритм устойчивой кластеризации с иcпользованием связей (robust clustering using links, ROCK) решает задачу кластеризации объектов по заранее заданному количеству [math]k[/math] кластеров. В пространстве объектов должна быть определена функция сходства/расстояния между объекта [math]sim(p_i, p_j)[/math]. Данный алгоритм относится к иерархическим методам кластеризации, который начинает с разбиения пространства на большое количество кластеров и постепенно объединяя их до нужного количества. Алгоритм пытается объединить в один кластер точки с максимальным числом общих соседей.
- Данный алгоритм хорошо подходит для объектов с категориальными признаками (то есть признаками, принимающими небольшое количество значений). С помощью этого алгоритма также часто решается задача поиска ассоциативных правил.
1.2 Математическое описание алгоритма
- Пусть дано множество объектов [math]P = \{p_1, \ldots , p_n\}[/math], натуральное число [math]k[/math], функция схожести [math]sim(p_i, p_j)[/math], пороговое значение [math]\theta : 0\leq\theta\leq 1[/math] и функция функция [math] f( \theta ) [/math].
- Результатом работы алгоритма является [math]k[/math] непересекающихся кластеров, делящих множество [math]P[/math].
- Две точки называются соседними, если [math]sim(p_i, p_j) \geq \theta[/math]
- Количеством общих соседей [math]link(p_i, p_j)[/math] называется число точек, являющимися соседними для точек [math]p_i, p_j[/math].
- Функцией связи между кластерами называется [math]link[C_i, C_j] = \sum_{\begin{smallmatrix}p_q\in C_i,\; p_r\in C_j\end{smallmatrix}}^{ } link(p_{q},p_r)[/math].
- Функцией качества является функция
- [math] g(C_i, C_j) = \frac{link[C_i,C_j]}{(n_i + n_j)^{1 + 2f(\theta )} - n_i^{1+2f(\theta )} - n_j^{1+2f(\theta )}}[/math], где [math]n_i[/math] - число объектов в кластере [math]C_i[/math].
- Алгоритм начинает работу, разбив всё пространство на [math]n[/math] кластеров.
- Затем на каждом шаге он вычисляет значение [math]g(C_i, C_j)[/math] для каждой пары кластеров и объединяет эти кластеры в один.
- Алгоритм ведёт свою работу до тех пор, пока не получит [math]k[/math] кластеров.
- В качестве функции [math]f( \theta )[/math] обычно используется функция [math]f(\theta ) = \frac{\theta - 1}{\theta + 1}[/math] , [math]n_i^{1+2f(\theta )}[/math] - ожидаемое число связей между парами объектов кластера [math]C_i[/math].
- Если все признаки категориальны, то в качестве функции схожести можно использовать функцию:
- [math]sim(p_i,p_j) = \frac{|p_i\cap p_j|}{|p_i\cup p_j|}[/math], где [math]|p_i|[/math] - количество атрибутов в [math]p_i[/math]. Данная функция удобна в случае, если все признаки категориальны
- Если же признаки непрерывны, то можно использовать функции расстояний в многомерных пространствах, предварительно нормализовав признаки.
1.3 Вычислительное ядро алгоритма
- Вычислительное ядро алгоритма состоит из двух основных частей.
- Попарное вычисление связей между точками. Можно вычислить, умножив матрицу смежности саму на себя. Имеет квадратичную сложность от количества точек.
- Итеративное объединению кластеров. За [math]n-k[/math] шагов кластеры последовательно объединяются. Реализовывается с помощью структуры данных куча. Для каждого кластера math>i</math> хранится своя куча [math]q[i][/math], содержащая все связанный с ним кластеры, упорядоченная по убыванию функции качества. Также хранится глобальная куча [math]Q[/math], содержащая все кластеры [math]j[/math], упорядоченные по мере убывания функции качества [math]g(j, max(q[j]))[/math]. На каждом шаге итерации, после объединения кластеров требуется перестроить кучи объединённых кластеров в одну и перестроить глобальную кучу.
1.4 Макроструктура алгоритма
- Макроструктура состоит из последовательного выполнения двух шагов, описанных в описании ядра алгоритма:
- Построении матрицы связей
- Пересчёте куч и объединении кластеров
1.5 Схема реализации последовательного алгоритма
Описание реализации алгоритма на псевдокоде
1 procedure cluster(S, k)
2 begin
3 link := compute_links(S)
4 for s in S do
5 begin
6 q[s] := build_local_heap(link, s)
7 end
8 Q := build_global_heap(S, q)
9 while size(Q) > k do
10 begin
11 u := extract_max(Q)
12 v := max(q[u])
13 delete(Q, v)
14 w := merge(u, v)
15 for each x in q[u] or q[v] do
16 begin
17 link[x, w] := link[x, u] + link[x, v]
18 delete(q[x], u)
19 delete(q[x], v)
20 insert(q[x], w, g(x, w))
21 insert(q[w], x, g(x, w))
22 update(Q, x, q[x])
23 end
24 insert(Q, w, q[w])
25 deallocate(q[u])
26 deallocate(q[v])
27 end
28 end
1.6 Последовательная сложность алгоритма
- Временная сложность:
- Инициализация глобальной кучи - [math]O(n)[/math]
- Инициализация локальной кучи - требует [math]O(n)[/math]
- Вычисление связей между парой точек - в худшем случае алгоритмом Штрассена вычисляется за [math]O(n*n^{2.37})[/math], в среднем за [math]O(n m_\alpha m_m)[/math]
- Построение каждой кучи - [math] O(n)[/math]
- Сортировка каждой кучи - [math] O( n \log{} n)[/math]
- Основной цикл объединения кластеров выполняется в [math]n-k[/math] итераций.
- Вставить новый кластер в в [math] O(n)[/math] локальных куч размера [math] n[/math] - [math] O( n \log{} n)[/math]
Итого: [math] O(n^2 + n m_m m_a + n^2 \log{} n)[/math]
- Сложность по памяти:
- Поскольку каждая точка [math]i[/math] может иметь не более [math]\min \{ m_m m_i, n \} )[/math] связей, то общие затраты памяти не превышают [math] O(\min \{ n m_m m_a, n^2 \} )[/math].
- Хранение связей - [math] O(\min \{ n m_m m_a, n^2 \} )[/math] (поскольку каждая точка [math]i[/math] может иметь не более [math]\min \{ m_m m_i, n \} )[/math] связей)
Итого: [math] O(\min \{ n^2, n m_m m_a \} )[/math]
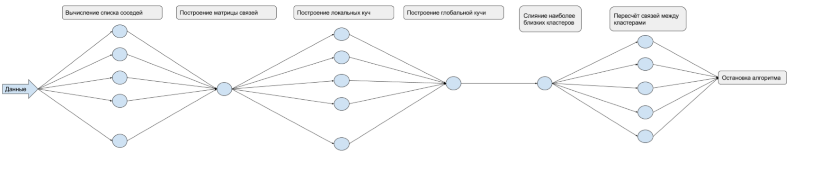
1.7 Информационный граф
1.8 Ресурс параллелизма алгоритма
- Вычисление соседей. Затраты данных операций при условии достаточного количества ядер [math]T_1 = O(n)[/math]
- Построения связей происходит в [math]n[/math] этапов, в каждом из которых нужно сделать [math]m[/math] расчетов(с учетом распараллеливания), где [math]m[/math] - количество соседей. В худшем случае [math]T_2 = O(n^2)[/math] в среднем случае [math]T_2 = O(n * m_a)[/math], где [math]m_a[/math] среднее ожидаемое число соседей.
- Построение одной кучи имеет сложность [math]O(n)[/math]. Для каждой кучи сортировка [math]O(n * log(n))[/math]. Итоговая сложность создания локальных куч [math]T_3 = O(n * log(n))[/math].
- Построение и сортировка глобальной кучи: [math]T_4 = O(n * log(n))[/math].
- В цикле происходит выбор кластеров, сливание, пересчет и обновление куч. Для всех элементов кучи слитых кластеров пересчитывается значение связи, вставляется в кучу выбранного кластера информация о новом кластере, удаляется старое. Сложность [math]O(log(n))[/math]. В худшем случае, одна итерация цикла происходит за [math]T_i = O(log(n))[/math]. Количество итераций n - k. Итого: [math]T_5 = O((n - k) * log(n))[/math]. При k = 1, [math]T_5 = O(n * log(n))[/math]
Итоговая сложность в худшем случае равна:
- [math]T_1 + T_2 + T_3 + T_4 + T_5 = O(n) + O(n^2) + O(n * log(n)) + O(n * log(n)) + O(n * log(n)) = O(n^2)[/math]
Итоговая сложность в среднем случае равна:
- [math]O(n * m_a) + O(n * log(n))[/math].
Сложность по времени:
- [math]O(n * (m_a + log(n)))[/math].
1.9 Входные и выходные данные алгоритма
- Входные данные алгоритма:
- Множество объектов [math]P = \{p_1, \ldots , p_n\}[/math]
- Целевое количество кластеров [math]k[/math]
- Гиперпараметры алгоритма:
- Функция схожести [math]sim(p_i, p_j)[/math]
- Пороговое значение схожести [math]\theta : 0\leq\theta\leq 1[/math]
- Функция ожидания количества соседей [math] f( \theta ) [/math]
- Результат:
- Метка кластера для каждого объекта
1.10 Свойства алгоритма
- Детерменированность алгоритма
- Отношение последовательной и параллельной сложностей: [math]\frac{O(n^2+nm_m m_\alpha + n^2\log n)}{O(\frac{n^2}{p}+nm_m m_\alpha + \frac{n^2\log n}{p})}[/math].
- Вычислительная сложность: [math]\frac{O(n^2+nm_m m_\alpha + n^2\log n)}{2n+2}[/math].