|
|
| (не показаны 94 промежуточные версии 4 участников) |
| Строка 1: |
Строка 1: |
| − | Данный документ содержит описание схемы, по которой предлагается описывать свойства и структуру каждого алгоритма. Описание состоит из двух частей. В [[#ЧАСТЬ. Свойства и структура алгоритмов|первой части]] описываются собственно алгоритмы и их свойства, а [[#ЧАСТЬ. Программная реализация алгоритмов|вторая]] посвящена описанию особенностей их программной реализации с учетом конкретных программно-аппаратных платформ. Такое деление на части сделано для того, чтобы машинно-независимые свойства алгоритмов, которые определяют качество их реализации на параллельных вычислительных системах, были бы выделены и описаны отдельно от множества вопросов, связанных с последующими этапами программирования алгоритмов и исполнения результирующих программ.
| + | {{Assignment|Coctic|Chalker}} |
| | + | {{algorithm |
| | + | | name = Нечеткий алгоритм С-средних (Fuzzy C-means) |
| | + | | serial_complexity = <math>O(c^2 MI + cMnI), (I</math> - число итераций, <math>c</math> - количество кластеров, <math>M</math> - число точек, <math>n</math> - размерность точек (свойств на объект)<math>)</math> |
| | + | | input_data = <math>Mn</math> |
| | + | | output_data = <math>cM</math> |
| | + | | pf_height = <math> O(c^2 I + cnI)</math> |
| | + | | pf_width = <math>O( M )</math> |
| | + | }} |
| | | | |
| − | Общая схема описания алгоритмов имеет следующий вид:
| + | Авторы: [[Участник:Nikmedoed|Н.А. Муромцев]] - перенос в вики, раздел 2, картинки, [[Участник:illusive_mike|М.С. Дворецкий]] - раздел 1 |
| | + | |
| | + | '''Нечеткий алгоритм С-средних''' (''Fuzzy C-means'') - позволяет получить нечёткую кластеризацию больших наборов числовых данных, что позволяет корректно определять объекты на границах кластеров. Однако, выполнение данного алгоритма требует серьёзных вычислительных ресурсов, а также изначального задания количества кластеров. Кроме того, может возникнуть неоднозначность с объектами, удалёнными от центров всех кластеров. |
| | + | |
| | + | |
| | + | = Свойства и структура алгоритмов = |
| | | | |
| − | = ЧАСТЬ. Свойства и структура алгоритмов =
| |
| − | Свойства алгоритмов никак не зависят от вычислительных систем, и с этой точки зрения данная часть AlgoWiki имеет безусловную собственную ценность. Описание алгоритма делается один раз, после чего многократно используется для его реализации в различных программно-аппаратных средах. Несмотря на то, что в данной части мы рассматриваем лишь машинно-независимые свойства алгоритмов, соображения, важные на этапе реализации, или же ссылки на соответствующие пункты [[#ЧАСТЬ. Программная реализация алгоритмов|части II AlgoWiki]], здесь также вполне уместны.
| |
| | | | |
| | == Общее описание алгоритма == | | == Общее описание алгоритма == |
| − | В данном разделе представляется самый первый вариант описания тех задач (или классов задач), для решения которых предназначен алгоритм. В описании поясняются особенности как алгоритма, так и объектов, с которыми он работает. Если описание соответствует целому классу схожих по структуре алгоритмов, либо же посвящено описанию отдельного представителя некоторого класса, то это здесь указывается явно. Описываются базовые математические свойства и структура входных данных. При необходимости, в описании могут присутствовать формулы, а также даваться ссылки на описания других используемых алгоритмов. Данное описание должно быть достаточным для однозначного понимания сути решаемой задачи.
| + | Алгоритм кластеризации Fuzzy C-Means (FCM) был предложен Дж. Данном в 1973 году <ref>Dunn, J.C.: A Fuzzy Relative of the ISODATA Process and Its Use in Detecting Compact Well-Separated Clusters. Journal of Cybernetics. 3 (1973): 32–57</ref> и доработан Дж. Бездеком в 1981 году <ref>Bezdek, J.C.: Pattern Recognition with Fuzzy Objective Function Algorithms. Plenum Press, New York (1981). ISBN 0-306-40671-3</ref>. В отличие от большинства существующих алгоритмов кластеризации, данный алгоритм является нечётким – каждый из объектов не входит однозначно в какой-либо кластер, а принадлежит всем кластерам с различными степенями принадлежности. Это даёт преимущества в качестве разбиения в случаях, когда кластеры находятся близко друг к другу, и большое число точек находится на их границах. Однако ценой такой нечёткости служат большие вычислительные затраты, чем у таких чётких алгоритмов, как [[Hard C-Means]] и [[K-Means]], при сохранении таких их недостатков, как априорное определение числа кластеров и отсутствие гарантии глобальной оптимальности результата. |
| | | | |
| | == Математическое описание алгоритма == | | == Математическое описание алгоритма == |
| − | Приводится математическое описание решаемой задачи в виде совокупности формул и соотношений, как это принято в книгах и учебниках. По возможности, используются общепринятые обозначения и способы записи. Должны быть явно определены все использованные обозначения и описаны свойства входных данных. Представленное описание должно быть достаточным для однозначного понимания постановки решаемой задачи для человека, знающего математику.
| + | Исходные данные: массив объектов <math>{X_k}\in{\R^n}, k=\overline{1,M}</math>, число кластеров c, экспоненциальный вес <math>m\in{[1,\infty)}</math>, параметр останова <math>\varepsilon>0</math>. |
| | | | |
| − | == Вычислительное ядро алгоритма ==
| + | Вычисляемые данные: матрица разбиения <math>F</math> размера <math>M\times c</math> (элементы <math>\mu_{ki}\in[0,1]</math>, <math>\sum^{c}_{i=1} {\mu_{ki}} = 1</math>), центры кластеров <math>V_i</math>, расстояния <math>D_{ki}</math> между объектами и центрами кластеров. |
| − | В описываемом алгоритме выделяется и описывается [[глоссарий#Вычислительное ядро|''вычислительное ядро'']], т.е. та часть алгоритма, на которую приходится основное время работы алгоритма. Если в алгоритме несколько вычислительных ядер, то отдельно описывается каждое ядро. Описание может быть сделано в достаточно произвольной форме: словесной или с использованием языка математических формул. Вычислительное ядро может полностью совпадать с описываемым алгоритмом.
| |
| | | | |
| − | == Макроструктура алгоритма ==
| + | '''Формулы метода (вычисляются последовательно на каждой итерации):''' |
| − | Если алгоритм использует в качестве составных частей другие алгоритмы, то это указывается в данном разделе. Если в дальнейшем имеет смысл описывать алгоритм не в максимально детализированном виде (т.е. на уровне арифметических операций), а давать только его макроструктуру, то здесь описывается структура и состав макроопераций. Если в других разделах описания данного алгоритма в рамках AlgoWiki используются введенные здесь макрооперации, то здесь даются пояснения, необходимые для однозначной интерпретации материала. Типичные варианты макроопераций, часто встречающиеся на практике: нахождение суммы элементов вектора, скалярное произведение векторов, умножение матрицы на вектор, решение системы линейных уравнений малого порядка, сортировка, вычисление значения функции в некоторой точке, поиск минимального значения в массиве, транспонирование матрицы, вычисление обратной матрицы и многие другие.
| |
| | | | |
| − | Описание макроструктуры очень полезно на практике. Параллельная структура алгоритмов может быть хорошо видна именно на макроуровне, в то время как максимально детальное отображение всех операций может сильно усложнить картину. Аналогичные аргументы касаются и многих вопросов реализации, и если для алгоритма эффективнее и/или технологичнее оставаться на макроуровне, оформив макровершину, например, в виде отдельной процедуры, то это и нужно отразить в данном разделе.
| + | 1. Уточнение центров кластеров по степеням принадлежности |
| − | Выбор макроопераций не однозначен, причем, выделяя различные макрооперации, можно делать акценты на различных свойствах алгоритмов. С этой точки зрения, в описании одного алгоритма может быть представлено несколько вариантов его макроструктуры, дающих дополнительную информацию о его структуре. На практике, подобные альтернативные формы представления макроструктуры алгоритма могут оказаться исключительно полезными для его эффективной реализации на различных вычислительных платформах.
| + | :<math> |
| | + | \begin{align} |
| | + | &V_i=\frac{\sum^{M}_{k=1} {\mu^m_{ki} * X_k}}{\sum^{M}_{k=1} {\mu^m_{ki}}},i=\overline{1,c} |
| | + | \end{align} |
| | + | </math> |
| | + | 2. Расчёт расстояний между новыми центрами кластеров и точками данных |
| | + | :<math> |
| | + | \begin{align} |
| | + | &D_{ki}=\sqrt{{\lVert X_k - V_i \rVert}^2},k=\overline{1,M},i=\overline{1,c} |
| | + | \end{align} |
| | + | </math> |
| | + | 3. Пересчёт степеней принадлежности объектов кластерам |
| | + | :<math> |
| | + | \begin{align} |
| | + | &\mu_{ki}=\frac{1}{{ \sum^{c}_{j=1} \left ( {\frac{D_{ki}}{D_{kj}}} \right ) }^{{2}/{m-1}} |
| | + | },k=\overline{1,M},i=\overline{1,c}\\ |
| | + | \end{align} |
| | + | </math> |
| | | | |
| − | == Схема реализации последовательного алгоритма ==
| + | На каждой итерации алгоритма происходит уточнение элементов матрицы <math>F</math>. Выходом алгоритма служит матрица <math>F</math>, к которой алгоритм сходится. Факт того, что алгоритм сошёлся, устанавливается проверкой вида <math>\max_{k = \overline{1,M},i = \overline{1,c}} {( \left | \mu_{ki} - \mu_{ki}^* \right |)} < \varepsilon</math> либо <math>\max_{i = \overline{1,c}} {( \left | V_i - V_i^* \right |)} < \varepsilon</math>, где <math>\mu_{ki}^* (V_i^*)</math> – значение <math>\mu_{ki}(V_i)</math>, вычисленное на предыдущей итерации. |
| − | Здесь описываются все шаги, которые нужно выполнить при последовательной реализации данного алгоритма. В некотором смысле, данный раздел является избыточным, поскольку математическое описание уже содержит всю необходимую информацию. Однако он, несомненно, полезен: схема реализации алгоритма выписывается явно, помогая однозначной интерпретации приводимых далее оценок и свойств.
| |
| | | | |
| − | Описание может быть выполнено в виде блок-схемы, последовательности математических формул, обращений к описанию других алгоритмов, фрагмента кода на Фортране, Си или другом языке программирования, фрагмента кода на псевдокоде и т.п. Главное - это сделать схему реализации последовательного алгоритма полностью понятной. Совершенно не обязательно все шаги детализировать до элементарных операций, отдельные шаги могут соответствовать макрооперациям, отвечающим другим алгоритмам.
| + | == Вычислительное ядро алгоритма == |
| | + | Вычислительное ядро алгоритма Fuzzy C-Means составляют шаги вычисления центров кластеров, расстояний между ними и точками данных и в особенности пересчёта матрицы степеней принадлежности точек данных. |
| | | | |
| − | Описание схемы реализации вполне может содержать и словесные пояснения, отражающие какие-либо тонкие нюансы самого алгоритма или его реализации. Уже в данном разделе можно сказать про возможный компромисс между объемом требуемой оперативной памяти и временем работы алгоритма, между используемыми структурами данных и степенью доступного параллелизма. В частности, часто возникает ситуация, когда можно ввести дополнительные временные массивы или же отказаться от использования специальных компактных схем хранения данных, увеличивая степень доступного параллелизма.
| + | При реализации алгоритма некоторые повторяющиеся вычисления могут быть устранены. Так, для шага вычисления центров кластеров величины <math>\mu_{ki}^m</math> могут вычисляться однократно и умножаться на <math>X_k</math> при включении в сумму, записанную в числителе. Для шага вычисления расстояний между центрами кластеров и точками, операция взятия квадратного корня не является обязательной, так как в дальнейшем на шаге вычисления степеней принадлежности можно непосредственно использовать квадраты этих расстояний, и сумма в знаменателе будет приобретать вид: |
| | | | |
| − | == Последовательная сложность алгоритма == | + | <math>\sum^{c}_{j=1} {\left ( \frac{D_{ki} ^ {2}}{D_{kj} ^ {2}} \right )}^{{1}/{m-1}}</math> |
| − | В данном разделе описания свойств алгоритма приводится оценка его [[глоссарий#Последовательная сложность|''последовательной сложности'']], т.е. числа операций, которые нужно выполнить при последовательном исполнении алгоритма (в соответствии с [[#Описание схемы реализации последовательного алгоритма|п.1.5]]). Для разных алгоритмов понятие операции, в терминах которой оценивается его сложность, может существенно различаться. Это могут быть операции для работы с вещественными числами, целыми числами, поразрядные операции, обращения в память, обновления элементов массива, элементарные функции, макрооперации и другие. В LU-разложении преобладают арифметические операции над вещественными числами, а для транспонирования матриц важны лишь обращения к памяти: это и должно найти отражение в описании.
| |
| | | | |
| − | Если выбор конкретного типа операций для оценки сложности алгоритма не очевиден, то нужно привести обоснование возможных вариантов. В некоторых случаях можно приводить оценку не всего алгоритма, а лишь его вычислительного ядра: в таком случае это нужно отметить, сославшись [[#Общее описание алгоритма|на п.1.1]].
| + | == Макроструктура алгоритма == |
| | + | Алгоритм включает в себя три основных этапа – вычисление центров кластеров, вычисление расстояний между центрами кластеров и точками данных (включающее в себя макрооперации вычитания векторов и вычисления их норм) и пересчёт матрицы принадлежности. |
| | | | |
| − | Например, сложность алгоритма суммирования элементов вектора сдваиванием равна <math>n-1</math>. Сложность быстрого преобразования Фурье (базовый алгоритм Кули-Тьюки) для векторов с длиной, равной степени двойки – <math>n\log_2n</math> операций комплексного сложения и <math>(n\log_2n)/2</math> операций комплексного умножения. Сложность базового алгоритма разложения Холецкого (точечный вариант для плотной симметричной и положительно-определенной матрицы) это <math>n</math> вычислений квадратного корня, <math>n(n-1)/2</math> операций деления, по <math>(n^3-n)/6</math> операций умножения и сложения (вычитания).
| + | == Схема реализации последовательного алгоритма == |
| | + | Последовательность исполнения алгоритма следующая: |
| | | | |
| − | == Информационный граф == | + | Инициализация происходит случайным заполнением матрицы принадлежности <math>F</math> с соблюдением условия нормировки <math>\sum_{i=1}^c {\mu_{ki} =1}</math> и переходом к шагу 1, либо случайным определением центров кластеров <math>V_i</math> и переходом к шагу 2. |
| − | Это очень важный раздел описания. Именно здесь можно показать (увидеть) как устроена параллельная структура алгоритма, для чего приводится описание и изображение его информационного графа ([[глоссарий#Граф алгоритма|''графа алгоритма'']] [1]). Для рисунков с изображением графа будут составлены рекомендации по их формированию, чтобы все информационные графы, внесенные в энциклопедию, можно было бы воспринимать и интерпретировать одинаково. Дополнительно можно привести полное параметрическое описание графа в терминах покрывающих функций [1].
| |
| | | | |
| − | Интересных вариантов для отражения информационной структуры алгоритмов много. Для каких-то алгоритмов нужно показать максимально подробную структуру, а иногда важнее макроструктура. Много информации несут разного рода проекции информационного графа, выделяя его регулярные составляющие и одновременно скрывая несущественные детали. Иногда оказывается полезным показать последовательность в изменении графа при изменении значений внешних переменных (например, размеров матриц): мы часто ожидаем "подобное" изменение информационного графа, но это изменение не всегда очевидно на практике.
| + | Далее осуществляются итерации, на каждой из которых производятся следующие вычисления: |
| | | | |
| − | В целом, задача изображения графа алгоритма весьма нетривиальна. Начнем с того, что это потенциально бесконечный граф, число вершин и дуг которого определяется значениями внешних переменных, а они могут быть весьма и весьма велики. В такой ситуации, как правило, спасают упомянутые выше соображения подобия, делающие графы для разных значений внешних переменных "похожими": почти всегда достаточно привести лишь один граф небольшого размера, добавив, что графы для остальных значений будут устроены "точно также". На практике, увы, не всегда все так просто, и здесь нужно быть аккуратным.
| + | # <math>V_i=\frac{\sum_{k=1}^{M} {\mu_{ki}^m * X_k}}{\sum_{k=1}^{M} {\mu_{ki}^m} },i=\overline{1,c}</math> |
| | + | # <math>D_{ki}=\sqrt{{\lVert X_k - V_i \rVert}^2},k=\overline{1,M},i=\overline{1,c}</math> |
| | + | # <math>\mu_{ki}=\frac{1}{{ \sum^{c}_{j=1} {\left ( \frac{D_{ki}}{D_{kj}} \right )} }^{{2}/{m-1}} |
| | + | },k=\overline{1,M},i=\overline{1,c}</math> |
| | | | |
| − | Далее, граф алгоритма - это потенциально многомерный объект. Наиболее естественная система координат для размещения вершин и дуг информационного графа опирается на структуру вложенности циклов в реализации алгоритма. Если глубина вложенности циклов не превышает трех, то и граф размещается в привычном трехмерном пространстве, однако для более сложных циклических конструкций с глубиной вложенности 4 и больше необходимы специальные методы представления и изображения графов.
| |
| | | | |
| − | В данном разделе AlgoWiki могут использоваться многие интересные возможности, которые еще подлежат обсуждению: возможность повернуть граф при его отображении на экране компьютера для выбора наиболее удобного угла обзора, разметка вершин по типу соответствующим им операций, отражение [[глоссарий#Ярусно-параллельная форма графа алгоритма|''ярусно-параллельной формы графа'']] и другие. Но в любом случае нужно не забывать главную задачу данного раздела - показать информационную структуру алгоритма так, чтобы стали понятны все его ключевые особенности, особенности параллельной структуры, особенности множеств дуг, участки регулярности и, напротив, участки с недерминированной структурой, зависящей от входных данных. | + | В конце каждой итерации проверяется условие останова вида <math>\max_{k = \overline{1,M},i = \overline{1,c}} {( \left | \mu_{ki} - \mu_{ki}^* \right |)} < \varepsilon</math>, либо <math>\max_{i = \overline{1,c}} {( \left | V_i - V_i^* \right |)} < \varepsilon</math>, где <math>\mu_{ki}^* (V_i^*)</math> – значение <math>\mu_{ki}(V_i)</math>, вычисленное на предыдущей итерации. Если условие не выполнено, осуществляется переход к шагу 1. |
| | | | |
| − | На рис.1 показана информационная структура алгоритма умножения матриц, на рис.2 - информационная структура одного из вариантов алгоритма решения систем линейных алгебраических уравнений с блочно-двухдиагональной матрицей.
| + | == Последовательная сложность алгоритма == |
| | + | При кластеризации <math>M</math> объектов данных, представленных точками в <math>\R^n</math>, на <math>c</math> кластеров, алгоритм Fuzzy C-Means в последовательном варианте имеет вычислительную сложность – <math>O(c^2 MI+cMnI)</math>, где <math>I</math> – число итераций. Если считать размерность данных <math>n</math> малой, то эта сложность сводится к <math>O(c^2 MI)</math>. Основной частью алгоритма в этом случае является пересчёт матрицы принадлежностей, требующий вычисления <math>cM</math> сумм из <math>c</math> слагаемых на каждой итерации. |
| | | | |
| − | [[file:Fig1.svg|thumb|center|300px|Рис.1. Информационная структура алгоритма умножения матриц]]
| + | == Информационный граф == |
| − | [[file:Fig2.svg|thumb|center|300px|Рис.2. Информационная структура одного из вариантов алгоритма решения систем линейных алгебраических уравнений с блочно-двухдиагональной матрицей]] | + | Приведён граф единичной итерации алгоритма в параллельном оптимизированном варианте (метод распараллеливания взят в <ref>Kwok, T., Smith, K., |
| | + | Lozano, S., Taniar, D.: [http://num-meth.srcc.msu.ru/zhurnal/tom_2012/pdf/v13r207.pdf Parallel Fuzzy c-Means Clustering for Large Data Sets], последнее обращение 25.10.2016</ref>): |
| | | | |
| − | == Ресурс параллелизма алгоритма == | + | [[File:C-means_paralle_graph.png|thumb|upright=2.5|frame|right|alt=Paralel Fuzzy C-Means|Каждая вершина данного графа соответствует операциям из алгоритма, указанным при помощи указанных формул. Каждый из p столбцов соответствует работе одного из процессов. Пометки справа указывают число повторений каждого узла в ходе одной итерации.]] |
| − | Здесь приводится оценка [[глоссарий#Параллельная сложность|''параллельной сложности'']] алгоритма: числа шагов, за которое можно выполнить данный алгоритм в предположении доступности неограниченного числа необходимых процессоров (функциональных устройств, вычислительных узлов, ядер и т.п.). Параллельная сложность алгоритма понимается как высота канонической ярусно-параллельной формы [1]. Необходимо указать, в терминах каких операций дается оценка. Необходимо описать сбалансированность параллельных шагов по числу и типу операций, что определяется шириной ярусов канонической ярусно-параллельной формы и составом операций на ярусах.
| |
| | | | |
| − | Параллелизм в алгоритме часто имеет естественную иерархическую структуру. Этот факт очень полезен на практике, и его необходимо отразить в описании. Как правило, подобная иерархическая структура параллелизма хорошо отражается в последовательной реализации алгоритма через циклический профиль результирующей программы (конечно же, с учетом графа вызовов), поэтому циклический профиль ([[#Описание схемы реализации последовательного алгоритма|п.1.5]]) вполне может быть использован и для отражения ресурса параллелизма.
| + | Раздел 1.8 уточняет, соответствуют ли эти повторения однотипным ярусам или точкам данных, вычисления для которых можно распараллелить и далее. |
| | | | |
| − | Для описания ресурса параллелизма алгоритма (ресурса параллелизма информационного графа) необходимо указать ключевые параллельные ветви в терминах [[глоссарий#Конечный параллелизм|''конечного'']] и [[глоссарий#Массовый параллелизм|''массового'']] параллелизма. Далеко не всегда ресурс параллелизма выражается просто, например, через [[глоссарий#Кооодинатный параллелизм|''координатный параллелизм'']] или, что то же самое, через независимость итераций некоторых циклов (да-да-да, циклы - это понятие, возникающее лишь на этапе реализации, но здесь все так связано… В данном случае, координатный параллелизм означает, что информационно независимые вершины лежат на гиперплоскостях, перпендикулярных одной из координатных осей). С этой точки зрения, не менее важен и ресурс [[глоссарий#Скошенный параллелизм|''скошенного параллелизма'']]. В отличие от координатного параллелизма, скошенный параллелизм намного сложнее использовать на практике, но знать о нем необходимо, поскольку иногда других вариантов и не остается: нужно оценить потенциал алгоритма, и лишь после этого, взвесив все альтернативы, принимать решение о конкретной параллельной реализации. Хорошей иллюстрацией может служить алгоритм, структура которого показана на рис.2: координатного параллелизма нет, но есть параллелизм скошенный, использование которого снижает сложность алгоритма с <math>n\times m</math> в последовательном случае до <math>(n+m-1)</math> в параллельном варианте.
| + | Каждый процесс обладает следующими данными: |
| | + | * координатами точек данных <math>X_k</math>, <math>k=\overline{1+q* \frac{M}{p},q*(\frac{M}{p}+1)}</math>, где <math>q</math> – номер процесса, |
| | + | * значениями <math>\mu_{ki}</math> степени принадлежности для своих точек (<math>k=\overline{1+q* \frac{M}{p},q*(\frac{M}{p} +1)}, i=\overline{1,c}</math>), |
| | + | * координатами центров кластеров <math>V_i</math>, <math>i=\overline{1,c}</math>. |
| | + | Суммы <math>\sum_{k=1+q*\frac{M}{p}}^{q * ( \frac{M}{p} +1 )} {\mu_{ki}^m}</math> и <math>\sum_{k=1+q*\frac{M}{p}}^{q * ( \frac{M}{p} +1 )} {\mu_{ki}^m X_k}</math> вычисляются одновременно, поэтому значения <math>\mu_{ki}^m</math> вычисляются по одному разу за итерацию. Таким образом, второй ярус операций на рисунке на деле не содержит операций возведения в степень. |
| | + | За счёт линейности большинства выражений относительно данных по точкам, процессы взаимодействуют только при редукции сумм, составляющих <math>V_i</math>. Всё остальное время каждый процессор работает только со своими <math>\frac{M}{p}</math> точками. Это обеспечивает применимость алгоритма для больших <math>M</math>. |
| | | | |
| − | Рассмотрим алгоритмы, последовательная сложность которых уже оценивалась в [[#Последовательная сложность алгоритма|п.1.6]]. Параллельная сложность алгоритма суммирования элементов вектора сдваиванием равна <math>\log_2n</math>, причем число операций на каждом ярусе убывает с <math>n/2</math> до <math>1</math>. Параллельная сложность быстрого преобразования Фурье (базовый алгоритм Кули-Тьюки) для векторов с длиной, равной степени двойки - <math>\log_2n</math>. Параллельная сложность базового алгоритма разложения Холецкого (точечный вариант для плотной симметричной и положительно-определенной матрицы) это <math>n</math> шагов для вычислений квадратного корня, <math>(n-1)</math> шагов для операций деления и <math>(n-1)</math> шагов для операций умножения и сложения.
| + | == Ресурс параллелизма алгоритма == |
| | + | При распараллеливании по точкам исходных данных и условии останову по малому изменению степеней принадлежности выполнение одной итерации алгоритма FCM может быть разделено на следующие ярусы: |
| | + | * <math>c</math> ярусов нахождения частичных сумм знаменателя (по <math>\frac{M}{p}-1</math> сложений, <math>\frac{M}{p}</math> операций возведения в степень на процесс), |
| | + | * <math>c</math> ярусов нахождения частичных сумм числителя (по <math>\frac{M}{p} -1</math> сложений, <math>\frac{M}{p}</math> умножений на процесс), |
| | + | * <math>2</math> редукции сумм и передач значений <math>V_i</math> процессам (получение <math>c(n+1)</math> значений, <math>cn</math> делений), |
| | + | * <math>c</math> ярусов вычисления расстояний до центров (по <math>n-1</math> сложений, <math>n</math> вычитаний, <math>n</math> умножений), каждый процесс получает <math>\frac{M}{p}</math> точек на обработку, |
| | + | * <math>c</math> ярусов вычисления степеней принадлежности точек (по <math>c+1</math> делений, c возведений в степень, <math>c-1</math> сложений), каждый процесс получает <math>\frac{M}{p}</math> точек на обработку, |
| | + | * до <math>c</math> ярусов проверки условий останова (по <math>1</math> вычитанию, <math>1</math> сравнению), каждый процесс получает <math>\frac{M}{p}</math> точек на обработку, |
| | + | * <math>1</math> редукция для обмена статусом завершения. |
| | + | Таким образом, при распараллеливании по точкам исходных данных при условии наличия в каждом узле достаточного объёма памяти для хранения всего массива координат центров кластеров высота и ширина ЯПФ алгоритма FCM равны соответственно <math>O(c^2 I+cnI)</math> и <math>O(M)</math>. |
| | | | |
| | == Входные и выходные данные алгоритма == | | == Входные и выходные данные алгоритма == |
| − | В данном разделе необходимо описать объем, структуру, особенности и свойства входных и выходных данных алгоритма: векторы, матрицы, скаляры, множества, плотные или разреженные структуры данных, их объем. Полезны предположения относительно диапазона значений или структуры, например, диагональное преобладание в структуре входных матриц, соотношение между размером матриц по отдельным размерностям, большое число матриц очень малой размерности, близость каких-то значений к машинному нулю, характер разреженности матриц и другие.
| + | '''Входные данные''': массив векторов <math>X_i</math>, число кластеров <math>c</math>, экспоненциальный вес <math>m\in{[1,\infty)}</math>, параметр останова <math>\varepsilon>0</math>. |
| | | | |
| − | == Свойства алгоритма ==
| + | '''Объём входных данных''': <math>Mn</math> для входных векторов, 3 вспомогательных параметра. |
| − | Описываются прочие свойства алгоритма, на которые имеет смысл обратить внимание на этапе реализации. Как и ранее, никакой привязки к конкретной программно-аппаратной платформе не предполагается, однако вопросы реализации в проекте AlgoWiki всегда превалируют, и необходимость обсуждения каких-либо свойств алгоритмов определяется именно этим.
| |
| | | | |
| − | Весьма полезным является ''соотношение последовательной и параллельной сложности'' алгоритма. Оба понятия мы рассматривали ранее, но здесь делается акцент на том выигрыше, который теоретически может дать параллельная реализация алгоритма. Не менее важно описать и те сложности, которые могут возникнуть в процессе получения параллельной версии алгоритма.
| + | '''Выходные данные''': матрица принадлежности <math>F</math> (элементы <math>\mu_{ki}\in[0,1]</math>). Условие нормировки: <math>\sum^{c}_{i=1} {\mu_{ki}} = 1</math>. |
| | | | |
| − | [[глоссарий#Вычислительная мощность|''Вычислительная мощность'']] алгоритма равна отношению числа операций к суммарному объему входных и выходных данных. Она показывает, сколько операций приходится на единицу переданных данных. Несмотря на простоту данного понятия, это значение исключительно полезно на практике: чем выше вычислительная мощность, тем меньше накладных расходов вызывает перемещение данных для их обработки, например, на сопроцессоре, ускорителе или другом узле кластера. Например, вычислительная мощность скалярного произведения двух векторов равна всего лишь <math>1</math>, а вычислительная мощность алгоритма умножения двух квадратных матриц равна <math>2n/3</math>.
| + | '''Объём выходных данных''': <math>cM</math>. |
| | | | |
| − | Вопрос первостепенной важности на последующем этапе реализации - это [[глоссарий#Устойчивость|''устойчивость'']] алгоритма. Все, что касается различных сторон этого понятия, в частности, оценки устойчивости, должно быть описано в данном разделе.
| + | == Свойства алгоритма == |
| − | | + | В случае неограниченного распараллеливания по точкам данных (1 процесс на точку), отношение последовательной сложности алгоритма к параллельной пропорционально <math>M</math>. |
| − | ''Сбалансированность'' вычислительного процесса можно рассматривать с разных сторон. Здесь и сбалансированность типов операций, в частности, арифметических операций между собой (сложение, умножение, деление) или же арифметических операций по отношению к операциям обращения к памяти (чтение/запись). Здесь и сбалансированность операций между параллельными ветвями алгоритма. С одной стороны, балансировка нагрузки является необходимым условием эффективной реализации алгоритма. Вместе с этим, это очень непростая задача, и в описании должно быть отмечено явно, насколько алгоритм обладает этой особенностью. Если обеспечение сбалансированности не очевидно, желательно описать возможные пути решения этой задачи.
| |
| − | | |
| − | На практике важна [[глоссарий#Детерминированность|''детерминированность алгоритмов'']], под которой будем понимать постоянство структуры вычислительного процесса. С этой точки зрения, классическое умножение плотных матриц является детерминированным алгоритмом, поскольку его структура при фиксированном размере матриц никак не зависит от элементов входных матриц. Умножение разреженных матриц, когда матрица хранятся в одном из специальных форматов, свойством детерминированности уже не обладает: его свойства, например, степень локальности данных зависит от структуры разреженности входных матриц. Итерационный алгоритм с выходом по точности также не является детерминированным: число итераций, а значит и число операций, меняется в зависимости от входных данных. В этом же ряду стоит использование датчиков случайных чисел, меняющих вычислительный процесс для различных запусков программы. Причина выделения свойства детерминированности понятна: работать с детерминированным алгоритмом проще, поскольку один раз найденная структура и будет определять качество его реализации. Если детерминированность нарушается, то это должно быть здесь описано вместе с описанием того, как недетерминированность влияет на структуру вычислительного процесса.
| |
| − | | |
| − | Серьезной причиной недетерминированности работы параллельных программ является изменение порядка выполнения ассоциативных операций. Типичный пример - это использование глобальных MPI-операций на множестве параллельных процессов, например, суммирование элементов распределенного массива. Система времени исполнения MPI сама выбирает порядок выполнения операций, предполагая выполнение свойства ассоциативности, из-за чего ошибки округления меняются от запуска программы к запуску, внося изменения в конечный результат ее работы. Это очень серьезная проблема, которая сегодня встречается часто на системах с массовым параллелизмом и определяет отсутствие повторяемости результатов работы параллельных программ. Данная особенность характерна для [[#ЧАСТЬ. Программная реализация алгоритмов|второй части AlgoWiki]], посвященной реализации алгоритмов, но вопрос очень важный, и соответствующие соображения, по возможности, должны быть отмечены и здесь.
| |
| − | | |
| − | Заметим, что, в некоторых случаях, недетерминированность в структуре алгоритмов можно "убрать" введением соответствующих макроопераций, после чего структура становится не только детерминированной, но и более понятной для восприятия. Подобное действие также следует отразить в данном разделе.
| |
| | | | |
| − | [[глоссарий#Степень исхода|''Степень исхода вершины информационного графа'']] показывает, в скольких операциях ее результат будет использоваться в качестве аргумента. Если степень исхода вершины велика, то на этапе реализации алгоритма нужно позаботиться об эффективном доступе к результату ее работы. В этом смысле, особый интерес представляют рассылки данных, когда результат выполнения одной операции используется во многих других вершинах графа, причем число таких вершин растет с увеличением значения внешних переменных.
| + | Параметр <math>m</math> задаёт степень «размытости» кластеров. В отсутствие априорных данных его обычно берут равным 2. В предельном случае сведения параметра <math>m</math> к значению 1, кластеры становятся чёткими и алгоритм вырождается в алгоритм кластеризации K-Means. |
| | | | |
| − | ''"Длинные" дуги в информационном графе'' [1] говорят о потенциальных сложностях с размещением данных в иерархии памяти компьютера на этапе выполнения программы. С одной стороны, длина дуги зависит от выбора конкретной системы координат, в которой расположены вершины графа, а потому в другой системе координат они попросту могут исчезнуть (но не появится ли одновременно других длинных дуг?). А с другой стороны, вне зависимости от системы координат их присутствие может быть сигналом о необходимости длительного хранения данных на определенном уровне иерархии, что накладывает дополнительные ограничения на эффективность реализации алгоритма. Одной из причин возникновения длинных дуг являются рассылки скалярных величин по всем итерациям какого-либо цикла: в таком виде длинные дуги не вызывают каких-либо серьезных проблем на практике.
| + | Алгоритм недетерминирован, начальное положение кластеров задаётся случайно либо явно, либо опосредованно (через матрицу принадлежности). Алгоритм сходится к локальному экстремуму <ref>Höppner, F., Klawonn, F.: [https://public.fh wolfenbuettel.de/~klawonn/Papers/hoeppnerklawonntfs03.pdf A Contribution to Convergence Theory of Fuzzy c-Means and Derivatives], Дата последнего обращения: 13.10.2016</ref> и, таким образом, не гарантирует оптимальный результат при случайном выборе начальных значений. |
| | | | |
| − | Для проектирования специализированных процессоров или реализации алгоритма на ПЛИС представляют интерес ''компактные укладки информационного графа'' [1], которые также имеет смысл привести в данном разделе.
| + | = Программная реализация алгоритма = |
| | | | |
| − | = ЧАСТЬ. Программная реализация алгоритма =
| |
| − | Вторая часть описания алгоритмов в рамках AlgoWiki рассматривает все составные части процесса их реализации. Рассматривается как последовательная реализация алгоритма, так и параллельная. Описывается взаимосвязь свойств программ, реализующих алгоритм, и особенностей архитектуры компьютера, на которой они выполняются. Исследуется работа с памятью, локальность данных и вычислений, описывается масштабируемость и эффективность параллельных программ, производительность компьютеров, достигаемая на данной программе. Обсуждаются особенности реализации для разных классов архитектур компьютеров, приводятся ссылки на реализации в существующих библиотеках.
| |
| | | | |
| | == Особенности реализации последовательного алгоритма == | | == Особенности реализации последовательного алгоритма == |
| − | Здесь описываются особенности и варианты реализации алгоритма в виде последовательной программы, которые влияют на [[глоссарий#Эффективность реализации|''эффективность ее выполнения'']]. В частности, в данном разделе имеет смысл ''сказать о существовании блочных вариантов реализации алгоритма'', дополнительно описав потенциальные преимущества или недостатки, сопровождающие такую реализацию. Важный вопрос - это ''возможные варианты организации работы с данными'', варианты структур данных, наборов временных массивов и другие подобные вопросы. Для различных вариантов реализации следует оценить доступный ресурс параллелизма и объем требуемой памяти.
| |
| − |
| |
| − | Важным нюансом является ''описание необходимой разрядности выполнения операций алгоритма'' (точности). На практике часто нет никакой необходимости выполнять все арифметические операции над вещественными числами с двойной точностью, т.к. это не влияет ни на устойчивость алгоритма, ни на точность получаемого результата. В таком случае, если значительную часть операций можно выполнять над типом float, и лишь в некоторых фрагментах необходим переход к типу double, это обязательно нужно отметить. Это прямое указание не только на правильную реализацию с точки зрения устойчивости по отношению к ошибкам округления, но и на более эффективную.
| |
| − |
| |
| − | Опираясь на информацию из [[#Описание ресурса параллелизма алгоритма|п.1.8]] (описание ресурса параллелизма алгоритма), при описании последовательной версии стоит сказать про возможности [[глоссарий#Эквивалентное преобразование|''эквивалентного преобразования программ'']], реализующих данных алгоритм. В дальнейшем, это даст возможность простого использования доступного параллелизма или же просто покажет, как использовать присущий алгоритму параллелизм на практике. Например, параллелизм на уровне итераций самого внутреннего цикла обычно используется для векторизации. Однако, в некоторых случаях этот параллелизм можно поднять "вверх" по структуре вложенности объемлющих циклов, что делает возможной и эффективную реализацию данного алгоритма на многоядерных SMP-компьютерах.
| |
| | | | |
| − | С этой же точки зрения, в данном разделе весьма полезны соображения по реализации алгоритма на различных параллельных вычислительных платформах. Высокопроизводительные кластеры, многоядерные узлы, возможности для векторизации или использования ускорителей - особенности этих архитектур не только опираются на разные свойства алгоритмов, но и по-разному должны быть выражены в программах, что также желательно описать в данном разделе.
| |
| | | | |
| | == [[Локальность данных и вычислений]] == | | == [[Локальность данных и вычислений]] == |
| − | Вопросы локальности данных и вычислений не часто изучаются на практике, но именно локальность определяет эффективность выполнения программ на современных вычислительных платформах [2, 3]. В данном разделе приводятся оценки степени [[глоссарий#Локальность использования данных|''локальности данных'']] и [[глоссарий#Локальность вычислений|вычислений]] в программе, причем рассматривается как [[глоссарий#Временная локальность|''временна́я'']], так и [[глоссарий#Пространственная локальность|''пространственная'']] локальность. Отмечаются позитивные и негативные факты, связанные с локальностью, какие ситуации и при каких условиях могут возникать. Исследуется, как меняется локальность при переходе от последовательной реализации к параллельной. Выделяются ключевые шаблоны взаимодействия программы, реализующей описываемый алгоритм, с памятью. Отмечается возможная взаимосвязь между используемыми конструкциями языков программирования и степенью локальности, которыми обладают результирующие программы.
| |
| | | | |
| − | Отдельно приводятся профили взаимодействия с памятью для вычислительных ядер и ключевых фрагментов. Если из-за большого числа обращений по общему профилю сложно понять реальную специфику взаимодействия программ с памятью, то проводится последовательная детализация и приводится серия профилей более мелкого масштаба.
| |
| | | | |
| − | На рис.3 и рис.4 показаны профили обращения в память для программ, реализующих разложение Холецкого и быстрое преобразование Фурье, по которым хорошо видна разница свойств локальности у данных алгоритмов.
| + | == Возможные способы и особенности параллельной реализации алгоритма == |
| | | | |
| − | [[file:Cholesky_locality1.jpg|thumb|center|700px|Рис.3 Реализация метода Холецкого. Общий профиль обращений в память]]
| |
| − | [[file:fft 1.PNG|thumb|center|700px|Рис.4 Нерекурсивная реализация БПФ для степеней двойки. Общий профиль обращений в память]]
| |
| | | | |
| − | == Возможные способы и особенности параллельной реализации алгоритма == | + | == Масштабируемость алгоритма и его реализации == |
| − | Раздел довольно обширный, в котором должны быть описаны основные факты и положения, формирующие параллельную программу. К их числу можно отнести:
| |
| − | * представленный иерархически ресурс параллелизма, опирающийся на структуру циклических конструкций и на граф вызовов программы;
| |
| − | * комбинацию (иерархию) массового параллелизма и параллелизма конечного;
| |
| − | * возможные способы распределения операций между процессами/нитями;
| |
| − | * возможные способы распределения данных;
| |
| − | * оценку количества операций, объёма и числа пересылок данных (как общего числа, так и в пересчёте на каждый параллельный процесс);
| |
| | | | |
| − | и другие. | + | [[File:График.png|thumb|upright=2.5|frame|right|alt=Paralel Fuzzy C-Means time to iteration|График зависимости времени выполнения итерации параллельного нечеткого алгоритма С-средних (Fuzzy C-means) от количества процессоров и количества кластеризуемых вершин]] |
| | | | |
| − | В этом же разделе должны быть даны рекомендации или сделаны комментарии относительно реализации алгоритма с помощью различных технологий параллельного программирования: MPI, OpenMP, CUDA или использования директив векторизации.
| + | [[File:Effect_parallel_fuzzy_c-means.png|thumb|upright=2.5|frame|right|alt=Paralel Fuzzy C-Means efficiency|График эффективности распараллеливания нечеткого алгоритма С-средних (Fuzzy C-means) в зависимости от количества процессоров и количества кластеризуемых вершин.]] |
| | | | |
| − | == Масштабируемость алгоритма и его реализации ==
| + | Исследование проведено на суперкомпьютере IBM Blue Gene/P<ref>[http://hpc.cs.msu.ru/bgp Описание вычислительного комплекса IBM Blue Gene/P]</ref>. |
| − | Задача данного раздела - показать пределы [[глоссарий#Масштабируемость|''масштабируемости'']] алгоритма на различных платформах. Очень важный раздел. Нужно выделить, описать и оценить влияние точек барьерной синхронизации, глобальных операций, операций сборки/разборки данных, привести оценки или провести исследование [[глоссарий#Сильная масштабируемость|''сильной'']] и [[глоссарий#Слабая масштабируемость|''слабой'']] масштабируемости алгоритма и его реализаций.
| + | Для исследования была использована последовательная реализация алгоритма и реализован её [https://github.com/IllusiveMike/Parallel-Fuzzy-C-means/tree/patch-1 параллельный вариант]<ref>[https://github.com/nikmedoed/Parallel-Fuzzy-C-means Параллельная реализация алгоритма Fuzzy C-Means]</ref>. |
| | + | Алгоритм обладает плохо исследованной сходимостью, но объем вычислений на итерации не зависит от значений данных, поэтому данное исследование масштабируемости было произведено для единичной итерации. |
| | | | |
| − | Масштабируемость алгоритма определяет свойства самого алгоритма безотносительно конкретных особенностей используемого компьютера. Она показывает, насколько параллельные свойства алгоритма позволяют использовать возможности растущего числа процессорных элементов. Масштабируемость параллельных программ определяется как относительно конкретного компьютера, так и относительно используемой технологии программирования, и в этом случае она показывает, насколько может вырасти реальная производительность данного компьютера на данной программе, записанной с помощью данной технологии программирования, при использовании бóльших вычислительных ресурсов (ядер, процессоров, вычислительных узлов).
| + | Для упрощения экспериментов было решено использовать количество вершин для кластеризации и количество процессов равное степени двойки, поэтому для каждого эксперимента были выбраны значения: |
| | + | * <math>2^v, v=\overline{0,9}</math>, для количества процессоров; |
| | + | * <math>2^w, w=\overline{10,20}</math>, для количества кластеризуемых вершин. |
| | | | |
| − | Ключевой момент данного раздела заключается в том, чтобы показать ''реальные параметры масштабируемости программы'' для данного алгоритма на различных вычислительных платформах в зависимости от числа процессоров и размера задачи [4]. При этом важно подобрать такое соотношение между числом процессоров и размером задачи, чтобы отразить все характерные точки в поведении параллельной программы, в частности, достижение максимальной производительности, а также тонкие эффекты, возникающие, например, из-за блочной структуры алгоритма или иерархии памяти.
| + | Для одного набора значений проводилось 4 эксперимента и результаты усреднялись. При повторных запусках экспериментов значения выходили те же самые. |
| | | | |
| − | На рис.5. показана масштабируемость классического алгоритма умножения плотных матриц в зависимости от числа процессоров и размера задачи. На графике хорошо видны области с большей производительностью, отвечающие уровням кэш-памяти.
| + | Полученные результаты говорят о хорошей масштабируемости реализации алгоритма. Для большинства экспериментов эффективность распараллеливания находится в пределах 100±3%. Высокая эффективность обуславливается тем, что данные равномерно распределены по процессорам и на каждой итерации требуется глобальная редукция всего <math>2c+1</math> значений (<math>c</math> значений числителей центроид кластеров, <math>c</math> значений знаменателей центроид кластеров и одно значение признака останова). Таким образом вычисления занимают значительно больше времени, чем взаимодействия между процессами, которые практически не приводят к простоям из-за хорошей балансировки. Спад эффективности при малом числе вершин и большом числе процессоров обуславливается тем, что с уменьшением числа вершин, обрабатываемых каждым процессором, растёт доля времени обмена данных между процессорами, не зависящего от числа вершин, как показано выше. |
| − | [[file:Масштабируемость перемножения матриц производительность.png|thumb|center|700px|Рис.5 Масштабируемость классического алгоритма умножения плотных матриц в зависимости от числа процессоров и размера задачи]]
| |
| | | | |
| | == Динамические характеристики и эффективность реализации алгоритма == | | == Динамические характеристики и эффективность реализации алгоритма == |
| − | Это объемный раздел AlgoWiki, поскольку оценка эффективности реализации алгоритма требует комплексного подхода [5], предполагающего аккуратный анализ всех этапов от архитектуры компьютера до самого алгоритма. Основная задача данного раздела заключается в том, чтобы оценить степень эффективности параллельных программ, реализующих данный алгоритм на различных платформах, в зависимости от числа процессоров и размера задачи. Эффективность в данном разделе понимается широко: это и [[глоссарий#Эффективность распараллеливания|''эффективность распараллеливания'']] программы, это и [[глоссарий#Эффективность реализации|''эффективность реализации'']] программ по отношению к пиковым показателям работы вычислительных систем.
| |
| | | | |
| − | Помимо собственно показателей эффективности, нужно описать и все основные причины, из-за которых эффективность работы параллельной программы на конкретной вычислительной платформе не удается сделать выше. Это не самая простая задача, поскольку на данный момент нет общепринятой методики и соответствующего инструментария, с помощью которых подобный анализ можно было бы провести. Требуется оценить и описать эффективность работы с памятью (особенности профиля взаимодействия программы с памятью), эффективность использования заложенного в алгоритм ресурса параллелизма, эффективность использования коммуникационной сети (особенности коммуникационного профиля), эффективность операций ввода/вывода и т.п. Иногда достаточно интегральных характеристик по работе программы, в некоторых случаях полезно показать данные мониторинга нижнего уровня, например, по загрузке процессора, кэш-промахам, интенсивности использования сети Infiniband и т.п. Хорошее представление о работе параллельной MPI-программы дают данные трассировки, полученные, например, с помощью системы Scalasca.
| |
| | | | |
| | == Выводы для классов архитектур == | | == Выводы для классов архитектур == |
| − | В данный раздел должны быть включены рекомендации по реализации алгоритма для разных классов архитектур. Если архитектура какого-либо компьютера или платформы обладает специфическими особенностями, влияющими на эффективность реализации, то это здесь нужно отметить.
| |
| | | | |
| − | На практике это сделать можно по-разному: либо все свести в один текущий раздел, либо же соответствующие факты сразу включать в предшествующие разделы, где они обсуждаются и необходимы по смыслу. В некоторых случаях, имеет смысл делать отдельные варианты всей [[#ЧАСТЬ. Программная реализация алгоритмов|части II]] AlgoWiki применительно к отдельным классам архитектур, оставляя общей машинно-независимую [[#ЧАСТЬ. Свойства и структура алгоритмов|часть I]]. В любом случае, важно указать и позитивные, и негативные факты по отношению к конкретным классам. Можно говорить о возможных вариантах оптимизации или даже о "трюках" в написании программ, ориентированных на целевые классы архитектур.
| |
| | | | |
| | == Существующие реализации алгоритма == | | == Существующие реализации алгоритма == |
| − | Для многих пар алгоритм+компьютер уже созданы хорошие реализации, которыми можно и нужно пользоваться на практике. Данный раздел предназначен для того, чтобы дать ссылки на основные существующие последовательные и параллельные реализации алгоритма, доступные для использования уже сейчас. Указывается, является ли реализация коммерческой или свободной, под какой лицензией распространяется, приводится местоположение дистрибутива и имеющихся описаний. Если есть информация об особенностях, достоинствах и/или недостатках различных реализаций, то это также нужно здесь указать. Хорошими примерами реализации многих алгоритмов являются MKL, ScaLAPACK, PETSc, FFTW, ATLAS, Magma и другие подобные библиотеки.
| + | * пакет MATLAB <ref>[http://www.mathworks.com/help/fuzzy/fcm.html Документация пакета MATLAB, функция fcm], последнее обращение 15.10.2016</ref> |
| | + | * Реализация алгоритма на POSTGRESQL <ref>[http://num-meth.srcc.msu.ru/zhurnal/tom_2012/pdf/v13r207.pdf Реализация алгоритма Fuzzy C-means на POSTGRESQL], последнее обращение 15.10.2016</ref> |
| | | | |
| | = Литература = | | = Литература = |
| − | [1] Воеводин В.В., Воеводин Вл.В. Параллельные вычисления. - СПб.: БХВ-Петербург, 2002. - 608 с.
| |
| − |
| |
| − | [2] Воеводин В.В., Воеводин Вад.В. Спасительная локальность суперкомпьютеров //Открытые системы. - 2013. - № 9. - С. 12-15.
| |
| − |
| |
| − | [3] Воеводин Вад.В., Швец П. Метод покрытий для оценки локальности использования данных в программах // Вестник УГАТУ. — 2014. — Т. 18, № 1(62). — С. 224–229.
| |
| − |
| |
| − | [4] Антонов А.С., Теплов А.М. О практической сложности понятия масштабируемости параллельных программ// Высокопроизводительные параллельные вычисления на кластерных системах (HPC 2014): Материалы XIV Международной конференции -Пермь: Издательство ПНИПУ, 2014. С. 20-27.
| |
| − |
| |
| − | [5] Никитенко Д.А. Комплексный анализ производительности суперкомпьютерных систем, основанный на данных системного мониторинга // Вычислительные методы и программирование. 2014. 15. 85–97.
| |
| | | | |
| − | [[en:Description of algorithm properties and structure]] | + | [[en:Parallel Fuzzy c-Means Clustering]] |
| Нечеткий алгоритм С-средних (Fuzzy C-means)
|
| Последовательный алгоритм
|
| Последовательная сложность
|
[math]O(c^2 MI + cMnI), (I[/math] - число итераций, [math]c[/math] - количество кластеров, [math]M[/math] - число точек, [math]n[/math] - размерность точек (свойств на объект)[math])[/math]
|
| Объём входных данных
|
[math]Mn[/math]
|
| Объём выходных данных
|
[math]cM[/math]
|
| Параллельный алгоритм
|
| Высота ярусно-параллельной формы
|
[math] O(c^2 I + cnI)[/math]
|
| Ширина ярусно-параллельной формы
|
[math]O( M )[/math]
|
Авторы: Н.А. Муромцев - перенос в вики, раздел 2, картинки, М.С. Дворецкий - раздел 1
Нечеткий алгоритм С-средних (Fuzzy C-means) - позволяет получить нечёткую кластеризацию больших наборов числовых данных, что позволяет корректно определять объекты на границах кластеров. Однако, выполнение данного алгоритма требует серьёзных вычислительных ресурсов, а также изначального задания количества кластеров. Кроме того, может возникнуть неоднозначность с объектами, удалёнными от центров всех кластеров.
1 Свойства и структура алгоритмов
1.1 Общее описание алгоритма
Алгоритм кластеризации Fuzzy C-Means (FCM) был предложен Дж. Данном в 1973 году [1] и доработан Дж. Бездеком в 1981 году [2]. В отличие от большинства существующих алгоритмов кластеризации, данный алгоритм является нечётким – каждый из объектов не входит однозначно в какой-либо кластер, а принадлежит всем кластерам с различными степенями принадлежности. Это даёт преимущества в качестве разбиения в случаях, когда кластеры находятся близко друг к другу, и большое число точек находится на их границах. Однако ценой такой нечёткости служат большие вычислительные затраты, чем у таких чётких алгоритмов, как Hard C-Means и K-Means, при сохранении таких их недостатков, как априорное определение числа кластеров и отсутствие гарантии глобальной оптимальности результата.
1.2 Математическое описание алгоритма
Исходные данные: массив объектов [math]{X_k}\in{\R^n}, k=\overline{1,M}[/math], число кластеров c, экспоненциальный вес [math]m\in{[1,\infty)}[/math], параметр останова [math]\varepsilon\gt 0[/math].
Вычисляемые данные: матрица разбиения [math]F[/math] размера [math]M\times c[/math] (элементы [math]\mu_{ki}\in[0,1][/math], [math]\sum^{c}_{i=1} {\mu_{ki}} = 1[/math]), центры кластеров [math]V_i[/math], расстояния [math]D_{ki}[/math] между объектами и центрами кластеров.
Формулы метода (вычисляются последовательно на каждой итерации):
1. Уточнение центров кластеров по степеням принадлежности
- [math]
\begin{align}
&V_i=\frac{\sum^{M}_{k=1} {\mu^m_{ki} * X_k}}{\sum^{M}_{k=1} {\mu^m_{ki}}},i=\overline{1,c}
\end{align}
[/math]
2. Расчёт расстояний между новыми центрами кластеров и точками данных
- [math]
\begin{align}
&D_{ki}=\sqrt{{\lVert X_k - V_i \rVert}^2},k=\overline{1,M},i=\overline{1,c}
\end{align}
[/math]
3. Пересчёт степеней принадлежности объектов кластерам
- [math]
\begin{align}
&\mu_{ki}=\frac{1}{{ \sum^{c}_{j=1} \left ( {\frac{D_{ki}}{D_{kj}}} \right ) }^{{2}/{m-1}}
},k=\overline{1,M},i=\overline{1,c}\\
\end{align}
[/math]
На каждой итерации алгоритма происходит уточнение элементов матрицы [math]F[/math]. Выходом алгоритма служит матрица [math]F[/math], к которой алгоритм сходится. Факт того, что алгоритм сошёлся, устанавливается проверкой вида [math]\max_{k = \overline{1,M},i = \overline{1,c}} {( \left | \mu_{ki} - \mu_{ki}^* \right |)} \lt \varepsilon[/math] либо [math]\max_{i = \overline{1,c}} {( \left | V_i - V_i^* \right |)} \lt \varepsilon[/math], где [math]\mu_{ki}^* (V_i^*)[/math] – значение [math]\mu_{ki}(V_i)[/math], вычисленное на предыдущей итерации.
1.3 Вычислительное ядро алгоритма
Вычислительное ядро алгоритма Fuzzy C-Means составляют шаги вычисления центров кластеров, расстояний между ними и точками данных и в особенности пересчёта матрицы степеней принадлежности точек данных.
При реализации алгоритма некоторые повторяющиеся вычисления могут быть устранены. Так, для шага вычисления центров кластеров величины [math]\mu_{ki}^m[/math] могут вычисляться однократно и умножаться на [math]X_k[/math] при включении в сумму, записанную в числителе. Для шага вычисления расстояний между центрами кластеров и точками, операция взятия квадратного корня не является обязательной, так как в дальнейшем на шаге вычисления степеней принадлежности можно непосредственно использовать квадраты этих расстояний, и сумма в знаменателе будет приобретать вид:
[math]\sum^{c}_{j=1} {\left ( \frac{D_{ki} ^ {2}}{D_{kj} ^ {2}} \right )}^{{1}/{m-1}}[/math]
1.4 Макроструктура алгоритма
Алгоритм включает в себя три основных этапа – вычисление центров кластеров, вычисление расстояний между центрами кластеров и точками данных (включающее в себя макрооперации вычитания векторов и вычисления их норм) и пересчёт матрицы принадлежности.
1.5 Схема реализации последовательного алгоритма
Последовательность исполнения алгоритма следующая:
Инициализация происходит случайным заполнением матрицы принадлежности [math]F[/math] с соблюдением условия нормировки [math]\sum_{i=1}^c {\mu_{ki} =1}[/math] и переходом к шагу 1, либо случайным определением центров кластеров [math]V_i[/math] и переходом к шагу 2.
Далее осуществляются итерации, на каждой из которых производятся следующие вычисления:
- [math]V_i=\frac{\sum_{k=1}^{M} {\mu_{ki}^m * X_k}}{\sum_{k=1}^{M} {\mu_{ki}^m} },i=\overline{1,c}[/math]
- [math]D_{ki}=\sqrt{{\lVert X_k - V_i \rVert}^2},k=\overline{1,M},i=\overline{1,c}[/math]
- [math]\mu_{ki}=\frac{1}{{ \sum^{c}_{j=1} {\left ( \frac{D_{ki}}{D_{kj}} \right )} }^{{2}/{m-1}}
},k=\overline{1,M},i=\overline{1,c}[/math]
В конце каждой итерации проверяется условие останова вида [math]\max_{k = \overline{1,M},i = \overline{1,c}} {( \left | \mu_{ki} - \mu_{ki}^* \right |)} \lt \varepsilon[/math], либо [math]\max_{i = \overline{1,c}} {( \left | V_i - V_i^* \right |)} \lt \varepsilon[/math], где [math]\mu_{ki}^* (V_i^*)[/math] – значение [math]\mu_{ki}(V_i)[/math], вычисленное на предыдущей итерации. Если условие не выполнено, осуществляется переход к шагу 1.
1.6 Последовательная сложность алгоритма
При кластеризации [math]M[/math] объектов данных, представленных точками в [math]\R^n[/math], на [math]c[/math] кластеров, алгоритм Fuzzy C-Means в последовательном варианте имеет вычислительную сложность – [math]O(c^2 MI+cMnI)[/math], где [math]I[/math] – число итераций. Если считать размерность данных [math]n[/math] малой, то эта сложность сводится к [math]O(c^2 MI)[/math]. Основной частью алгоритма в этом случае является пересчёт матрицы принадлежностей, требующий вычисления [math]cM[/math] сумм из [math]c[/math] слагаемых на каждой итерации.
1.7 Информационный граф
Приведён граф единичной итерации алгоритма в параллельном оптимизированном варианте (метод распараллеливания взят в [3]):
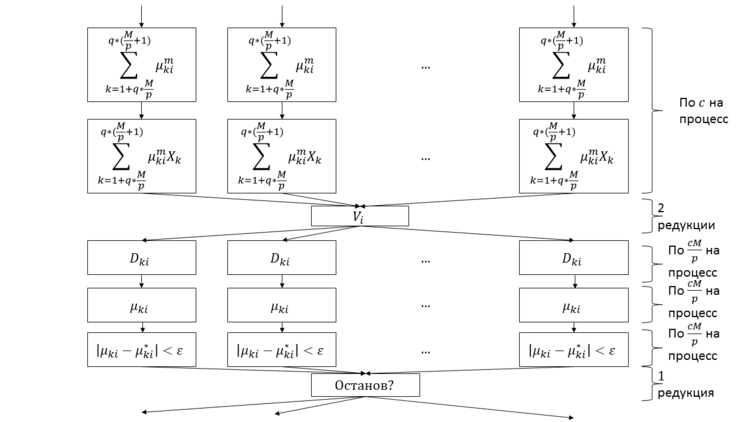
Каждая вершина данного графа соответствует операциям из алгоритма, указанным при помощи указанных формул. Каждый из p столбцов соответствует работе одного из процессов. Пометки справа указывают число повторений каждого узла в ходе одной итерации.
Раздел 1.8 уточняет, соответствуют ли эти повторения однотипным ярусам или точкам данных, вычисления для которых можно распараллелить и далее.
Каждый процесс обладает следующими данными:
- координатами точек данных [math]X_k[/math], [math]k=\overline{1+q* \frac{M}{p},q*(\frac{M}{p}+1)}[/math], где [math]q[/math] – номер процесса,
- значениями [math]\mu_{ki}[/math] степени принадлежности для своих точек ([math]k=\overline{1+q* \frac{M}{p},q*(\frac{M}{p} +1)}, i=\overline{1,c}[/math]),
- координатами центров кластеров [math]V_i[/math], [math]i=\overline{1,c}[/math].
Суммы [math]\sum_{k=1+q*\frac{M}{p}}^{q * ( \frac{M}{p} +1 )} {\mu_{ki}^m}[/math] и [math]\sum_{k=1+q*\frac{M}{p}}^{q * ( \frac{M}{p} +1 )} {\mu_{ki}^m X_k}[/math] вычисляются одновременно, поэтому значения [math]\mu_{ki}^m[/math] вычисляются по одному разу за итерацию. Таким образом, второй ярус операций на рисунке на деле не содержит операций возведения в степень.
За счёт линейности большинства выражений относительно данных по точкам, процессы взаимодействуют только при редукции сумм, составляющих [math]V_i[/math]. Всё остальное время каждый процессор работает только со своими [math]\frac{M}{p}[/math] точками. Это обеспечивает применимость алгоритма для больших [math]M[/math].
1.8 Ресурс параллелизма алгоритма
При распараллеливании по точкам исходных данных и условии останову по малому изменению степеней принадлежности выполнение одной итерации алгоритма FCM может быть разделено на следующие ярусы:
- [math]c[/math] ярусов нахождения частичных сумм знаменателя (по [math]\frac{M}{p}-1[/math] сложений, [math]\frac{M}{p}[/math] операций возведения в степень на процесс),
- [math]c[/math] ярусов нахождения частичных сумм числителя (по [math]\frac{M}{p} -1[/math] сложений, [math]\frac{M}{p}[/math] умножений на процесс),
- [math]2[/math] редукции сумм и передач значений [math]V_i[/math] процессам (получение [math]c(n+1)[/math] значений, [math]cn[/math] делений),
- [math]c[/math] ярусов вычисления расстояний до центров (по [math]n-1[/math] сложений, [math]n[/math] вычитаний, [math]n[/math] умножений), каждый процесс получает [math]\frac{M}{p}[/math] точек на обработку,
- [math]c[/math] ярусов вычисления степеней принадлежности точек (по [math]c+1[/math] делений, c возведений в степень, [math]c-1[/math] сложений), каждый процесс получает [math]\frac{M}{p}[/math] точек на обработку,
- до [math]c[/math] ярусов проверки условий останова (по [math]1[/math] вычитанию, [math]1[/math] сравнению), каждый процесс получает [math]\frac{M}{p}[/math] точек на обработку,
- [math]1[/math] редукция для обмена статусом завершения.
Таким образом, при распараллеливании по точкам исходных данных при условии наличия в каждом узле достаточного объёма памяти для хранения всего массива координат центров кластеров высота и ширина ЯПФ алгоритма FCM равны соответственно [math]O(c^2 I+cnI)[/math] и [math]O(M)[/math].
1.9 Входные и выходные данные алгоритма
Входные данные: массив векторов [math]X_i[/math], число кластеров [math]c[/math], экспоненциальный вес [math]m\in{[1,\infty)}[/math], параметр останова [math]\varepsilon\gt 0[/math].
Объём входных данных: [math]Mn[/math] для входных векторов, 3 вспомогательных параметра.
Выходные данные: матрица принадлежности [math]F[/math] (элементы [math]\mu_{ki}\in[0,1][/math]). Условие нормировки: [math]\sum^{c}_{i=1} {\mu_{ki}} = 1[/math].
Объём выходных данных: [math]cM[/math].
1.10 Свойства алгоритма
В случае неограниченного распараллеливания по точкам данных (1 процесс на точку), отношение последовательной сложности алгоритма к параллельной пропорционально [math]M[/math].
Параметр [math]m[/math] задаёт степень «размытости» кластеров. В отсутствие априорных данных его обычно берут равным 2. В предельном случае сведения параметра [math]m[/math] к значению 1, кластеры становятся чёткими и алгоритм вырождается в алгоритм кластеризации K-Means.
Алгоритм недетерминирован, начальное положение кластеров задаётся случайно либо явно, либо опосредованно (через матрицу принадлежности). Алгоритм сходится к локальному экстремуму [4] и, таким образом, не гарантирует оптимальный результат при случайном выборе начальных значений.
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
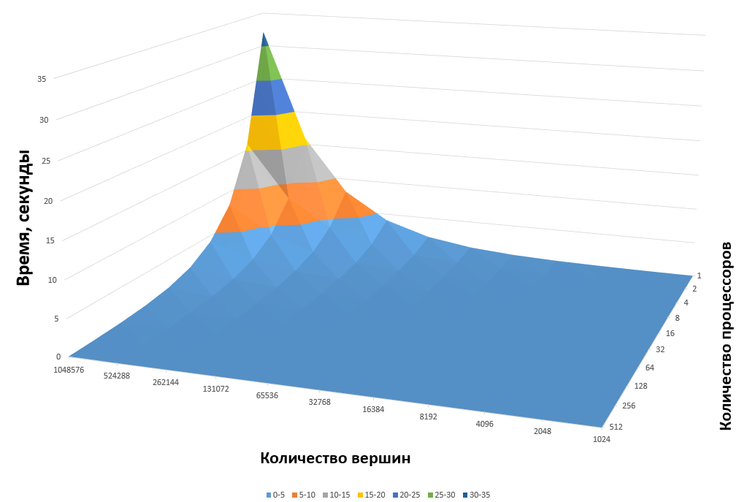
График зависимости времени выполнения итерации параллельного нечеткого алгоритма С-средних (Fuzzy C-means) от количества процессоров и количества кластеризуемых вершин
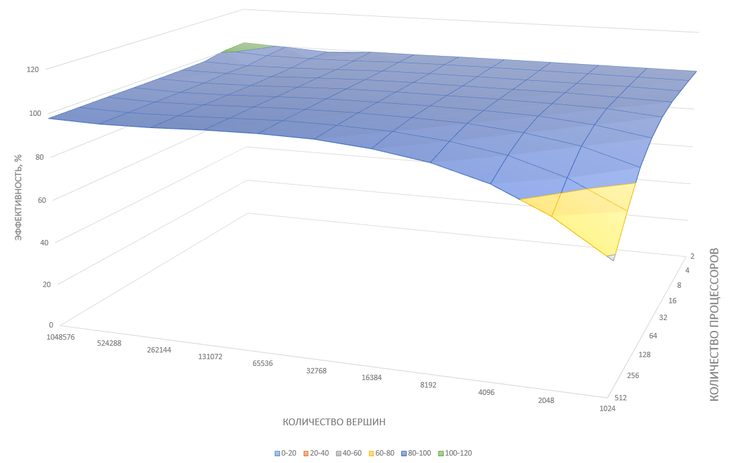
График эффективности распараллеливания нечеткого алгоритма С-средних (Fuzzy C-means) в зависимости от количества процессоров и количества кластеризуемых вершин.
Исследование проведено на суперкомпьютере IBM Blue Gene/P[5].
Для исследования была использована последовательная реализация алгоритма и реализован её параллельный вариант[6].
Алгоритм обладает плохо исследованной сходимостью, но объем вычислений на итерации не зависит от значений данных, поэтому данное исследование масштабируемости было произведено для единичной итерации.
Для упрощения экспериментов было решено использовать количество вершин для кластеризации и количество процессов равное степени двойки, поэтому для каждого эксперимента были выбраны значения:
- [math]2^v, v=\overline{0,9}[/math], для количества процессоров;
- [math]2^w, w=\overline{10,20}[/math], для количества кластеризуемых вершин.
Для одного набора значений проводилось 4 эксперимента и результаты усреднялись. При повторных запусках экспериментов значения выходили те же самые.
Полученные результаты говорят о хорошей масштабируемости реализации алгоритма. Для большинства экспериментов эффективность распараллеливания находится в пределах 100±3%. Высокая эффективность обуславливается тем, что данные равномерно распределены по процессорам и на каждой итерации требуется глобальная редукция всего [math]2c+1[/math] значений ([math]c[/math] значений числителей центроид кластеров, [math]c[/math] значений знаменателей центроид кластеров и одно значение признака останова). Таким образом вычисления занимают значительно больше времени, чем взаимодействия между процессами, которые практически не приводят к простоям из-за хорошей балансировки. Спад эффективности при малом числе вершин и большом числе процессоров обуславливается тем, что с уменьшением числа вершин, обрабатываемых каждым процессором, растёт доля времени обмена данных между процессорами, не зависящего от числа вершин, как показано выше.
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
- пакет MATLAB [7]
- Реализация алгоритма на POSTGRESQL [8]
3 Литература
- ↑ Dunn, J.C.: A Fuzzy Relative of the ISODATA Process and Its Use in Detecting Compact Well-Separated Clusters. Journal of Cybernetics. 3 (1973): 32–57
- ↑ Bezdek, J.C.: Pattern Recognition with Fuzzy Objective Function Algorithms. Plenum Press, New York (1981). ISBN 0-306-40671-3
- ↑ Kwok, T., Smith, K.,
Lozano, S., Taniar, D.: Parallel Fuzzy c-Means Clustering for Large Data Sets, последнее обращение 25.10.2016
- ↑ Höppner, F., Klawonn, F.: wolfenbuettel.de/~klawonn/Papers/hoeppnerklawonntfs03.pdf A Contribution to Convergence Theory of Fuzzy c-Means and Derivatives, Дата последнего обращения: 13.10.2016
- ↑ Описание вычислительного комплекса IBM Blue Gene/P
- ↑ Параллельная реализация алгоритма Fuzzy C-Means
- ↑ Документация пакета MATLAB, функция fcm, последнее обращение 15.10.2016
- ↑ Реализация алгоритма Fuzzy C-means на POSTGRESQL, последнее обращение 15.10.2016



