Участник:Viktorrulev/Алгоритм устойчивой кластеризации с иcпользованием связей: различия между версиями
ASA (обсуждение | вклад) |
|||
| (не показана 51 промежуточная версия 3 участников) | |||
| Строка 1: | Строка 1: | ||
| + | {{Assignment|Teplov}} | ||
| + | |||
{{algorithm | {{algorithm | ||
| name = Алгоритм устойчивой кластеризации с иcпользованием связей | | name = Алгоритм устойчивой кластеризации с иcпользованием связей | ||
| − | | serial_complexity = <math>O(M^2 + M^{ | + | | serial_complexity = <math>O(M^2 + M^2m_{nbr} + M^{2}logM)</math> |
| − | | pf_height = <math> | + | | pf_height = <math>O(MlogM)</math> |
| − | | pf_width = <math> | + | | pf_width = <math>O(M^2)</math> |
| input_data = <math>M \times N</math> | | input_data = <math>M \times N</math> | ||
| output_data = <math>M</math> | | output_data = <math>M</math> | ||
| Строка 14: | Строка 16: | ||
=== Общее описание алгоритма === | === Общее описание алгоритма === | ||
| − | Кластеризация (кластерный анализ) — задача разбиения заданной выборки объектов на непересекающиеся подмножества, называемые кластерами, так, чтобы каждый кластер состоял из схожих объектов, а объекты разных кластеров существенно отличались. Каждый объект из выборки характеризуется рядом признаков, которые могут быть вещественными, целочисленными, категорийными (то есть принимающими значения из какого-либо множества) | + | Кластеризация (кластерный анализ) — задача разбиения заданной выборки объектов на непересекающиеся подмножества, называемые кластерами, так, чтобы каждый кластер состоял из схожих объектов, а объекты разных кластеров существенно отличались. Каждый объект из выборки характеризуется рядом признаков, которые могут быть вещественными, целочисленными, категорийными (то есть принимающими значения из какого-либо конечного множества), бинарными (принимающими только два значения, обычно <math>true</math> или <math>false</math>). |
| − | '''Алгоритм устойчивой кластеризации с иcпользованием связей (robust clustering using links, ROCK)''' был предложен в 2000 году Sudipto Guha (Stanford University), Rajeev Rastogi (Bell Laboratories) и Kyuseok Shim (Bell Laboratories) <ref>Sudipto Guha, Rajeev Rastogi, Kyuseok Shim ROCK: A robust clustering algorithm for categorical attributes. 2000. Information Systems. Vol 25, Issue 5, Pages 345-366</ref> для кластеризации объектов с | + | '''Алгоритм устойчивой кластеризации с иcпользованием связей (robust clustering using links, ROCK)''' был предложен в 2000 году Sudipto Guha (Stanford University), Rajeev Rastogi (Bell Laboratories) и Kyuseok Shim (Bell Laboratories) <ref>Sudipto Guha, Rajeev Rastogi, Kyuseok Shim ROCK: A robust clustering algorithm for categorical attributes. 2000. Information Systems. Vol 25, Issue 5, Pages 345-366</ref> для кластеризации объектов с бинарными признаками. При этом алгоритм особенно эффективен, если у каждого объекта лишь небольшое количество признаков имеет значение <math>true</math>. |
| − | |||
| − | |||
=== Математическое описание алгоритма === | === Математическое описание алгоритма === | ||
| − | В ходе кластеризации <math>M</math> имеющихся | + | В ходе кластеризации <math>M</math> имеющихся объектов <math>P=\{p_1,...,p_M\}</math> (каждый объект имеет <math>N</math> признаков) должны быть разделены на <math>K</math> непересекающихся подмножеств (кластеров) <math>C_1, ..., C_K</math> таким образом, чтобы полученные кластеры максимизировали некоторую критериальную функцию <math>E(C_1, ..., C_K)</math>. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Будет называть два объекта <math>p_1</math> и <math>p_2</math> '''соседями''', если мера сходства <math>neighbour(p_1,p_2)</math> этих объектов больше некоторого заранее заданного порогового значения <math>\theta</math> В качестве меры сходства в алгоритме устойчивой кластеризации с использованием связей используется основанная на коэффициенте Жаккара мера сходства <math>sim(p_1,p_2)</math>. В ней <math>N(C_i)^{1+2f(\theta)}</math> имеет смысл ожидаемого (среднего) количества связей внутри одного кластера. | |
| − | <math> | + | '''Количеством связей''' <math>link(p_1,p_2)</math> между двумя объектами <math>p_1</math> и <math>p_2</math> будем называть количество общих соседей этих объектов. |
| − | Для того, чтобы сформировать кластеры, удовлетворяющие поставленному условию, необходимо последовательно объединять среди имеющихся кластеров такие пары кластеров, для которых метрика | + | Для того, чтобы сформировать кластеры, удовлетворяющие поставленному условию, необходимо последовательно объединять среди имеющихся кластеров такие пары кластеров, для которых метрика <math>goodness(C_i,C_j)</math> достигает максимального значения среди всех пар кластеров. На начальном этапе каждый объект считается отдельным кластером. |
| − | <math>goodness(C_i,C_j)=\frac {\sum_{p_r \in C_i, p_q \in C_j}{link(p_r,p_q)}} {(N(C_i) + N(C_j))^{1+2f(\theta)} - N(C_i)^{1+2f(\theta)} - N(C_j)^{1+2f(\theta)}}</math> | + | Формулы метода: |
| − | + | :<math> | |
| − | + | neighbour(p_1,p_2)=(sim(p_1,p_2)>\theta) | |
| + | </math> | ||
| + | <br> | ||
| + | :<math> | ||
| + | sim(p_1,p_2)=\frac{N(p_1 \cap p_2)}{N(p_1 \cup p_2)} | ||
| + | </math> | ||
| + | <br> | ||
| + | :<math> | ||
| + | link(p_1,p_2)=N \Big( \{ p \in P | sim(p_1,p) < \theta \} \cap \{ p \in P | sim(p_2,p) < \theta \} \Big) | ||
| + | </math> | ||
| + | <br> | ||
| + | :<math> | ||
| + | E(C_1,...,C_K)=\sum_{i=1}^{K}N(C_i) \ast \sum_{p_q,p_r \in C_i}\frac{link(p_q,p_r)}{N(C_i)^{1+2f(\theta)}} | ||
| + | </math> | ||
| + | <br> | ||
| + | :<math> | ||
| + | f(\theta)=\frac {1-\theta}{1+\theta} | ||
| + | </math> | ||
| + | <br> | ||
| + | :<math> | ||
| + | goodness(C_i,C_j)=\frac {\sum_{p_r \in C_i, p_q \in C_j}{link(p_r,p_q)}} {(N(C_i) + N(C_j))^{1+2f(\theta)} - N(C_i)^{1+2f(\theta)} - N(C_j)^{1+2f(\theta)}} | ||
| + | </math> | ||
=== Вычислительное ядро алгоритма === | === Вычислительное ядро алгоритма === | ||
| Строка 54: | Строка 59: | ||
Вычислительное ядро алгоритма можно разделить на два основных этапа: | Вычислительное ядро алгоритма можно разделить на два основных этапа: | ||
| − | # Вычисление количества связей между каждой парой | + | # Вычисление количества связей между каждой парой объектов (<math>\frac {M \times M} {2}</math> вычислений количества связей) |
# Последовательные объединения пар наиболее подходящих кластеров (<math>M-K</math> поисков пар и объединений) | # Последовательные объединения пар наиболее подходящих кластеров (<math>M-K</math> поисков пар и объединений) | ||
| Строка 63: | Строка 68: | ||
На макроуровне можно выделить следующие шаги алгоритма: | На макроуровне можно выделить следующие шаги алгоритма: | ||
| − | '''Шаг 1:''' вычисление соседних | + | '''Шаг 1:''' вычисление соседних объектов. |
| − | '''Шаг 2:''' вычисление количества связей между всеми | + | '''Шаг 2:''' вычисление количества связей между всеми объектами. |
'''Шаг 3:''' построение для каждого кластера упорядоченного списка значений метрики goodness со всеми остальными кластерами | '''Шаг 3:''' построение для каждого кластера упорядоченного списка значений метрики goodness со всеми остальными кластерами | ||
| Строка 79: | Строка 84: | ||
=== Схема реализации последовательного алгоритма === | === Схема реализации последовательного алгоритма === | ||
| − | + | Ниже приведен псевдокод схемы реализации последовательного алгоритма: | |
<source lang="pascal"> | <source lang="pascal"> | ||
| Строка 134: | Строка 139: | ||
'''Шаг 1:''' выполняется с помощью двух вложенных циклов и содержит <math>O(M^2)</math> операций | '''Шаг 1:''' выполняется с помощью двух вложенных циклов и содержит <math>O(M^2)</math> операций | ||
| − | '''Шаг 2:''' задача сводится к умножению полученной на предыдущем шаге матрицы соседства на саму себя. Это действие быть выполнено с помощью наивного метода за <math>O(M^3)</math> операций. | + | '''Шаг 2:''' задача сводится к умножению полученной на предыдущем шаге матрицы соседства на саму себя. Это действие быть выполнено с помощью наивного метода за <math>O(M^3)</math> операций. С помощью алгоритма Копперсмита — Винограда это можно сделать за <math>O(M^{2.37})</math> операций.<ref>Donald Coppersmith and Shmuel Winograd. Matrix multiplication via arithmetic progressions. In Proc. of the 19th Annual ACM Symposium on Theory of Computing. 1987.</ref> В случае, если среднее количество соседей каждого объекта значительно меньше общего количества объектов, связи могут быть вычислены за <math>O(M^2m_{nbr})</math>, где <math>m_{nbr}</math> - среднее количество соседей объекта. |
'''Шаг 3:''' имеет сложность <math>O(M)</math>.<ref>Thomas H. Cormen, Charles E. Leiserson, and Ronald L. Rivest. Introduction to | '''Шаг 3:''' имеет сложность <math>O(M)</math>.<ref>Thomas H. Cormen, Charles E. Leiserson, and Ronald L. Rivest. Introduction to | ||
Algorithms. The MIT Press, Massachusetts, 1990.</ref> | Algorithms. The MIT Press, Massachusetts, 1990.</ref> | ||
| − | '''Шаг 4:''' имеет | + | '''Шаг 4:''' имеет сложность <math>O(M)</math>. |
'''Шаг 5:''' вычислительная сложность каждой итерации цикла составляет <math>O(MlogM)</math>, так как в худшем случае в ходе итерации выполняется <math>M</math> вставок элемента в упорядоченный список. Желаемое количество кластеров <math>K</math> мало по сравнению с <math>M</math>, следовательно можно считать, что нужно выполнить <math>M</math> итераций цикла. Таким образом, общая вычислительная сложность цикла равна <math>O(M^{2}logM)</math>. | '''Шаг 5:''' вычислительная сложность каждой итерации цикла составляет <math>O(MlogM)</math>, так как в худшем случае в ходе итерации выполняется <math>M</math> вставок элемента в упорядоченный список. Желаемое количество кластеров <math>K</math> мало по сравнению с <math>M</math>, следовательно можно считать, что нужно выполнить <math>M</math> итераций цикла. Таким образом, общая вычислительная сложность цикла равна <math>O(M^{2}logM)</math>. | ||
| − | Таким образом, общую последовательную сложность алгоритма можно оценить, как <math>O(M^2 + M^{2.37} + M^{2}logM)</math> или <math>O(M^2 + M^2m_{nbr} + M^{2}logM)</math>. | + | Таким образом, общую последовательную сложность алгоритма в общем случае можно оценить, как |
| + | |||
| + | :<math>O(M^2 + M^{2.37} + M^{2}logM)</math> | ||
| + | |||
| + | или в случае небольшого количества соседних объектов для каждого объекта выборки, как | ||
| + | |||
| + | :<math>O(M^2 + M^2m_{nbr} + M^{2}logM)</math>. | ||
=== Информационный граф === | === Информационный граф === | ||
| − | ( | + | ''Информационный граф перемножения плотных матриц с подробным описанием представлен в статье [[Перемножение_плотных_неособенных_матриц_(последовательный_вещественный_вариант)|перемножение плотных матриц]]'' |
| + | |||
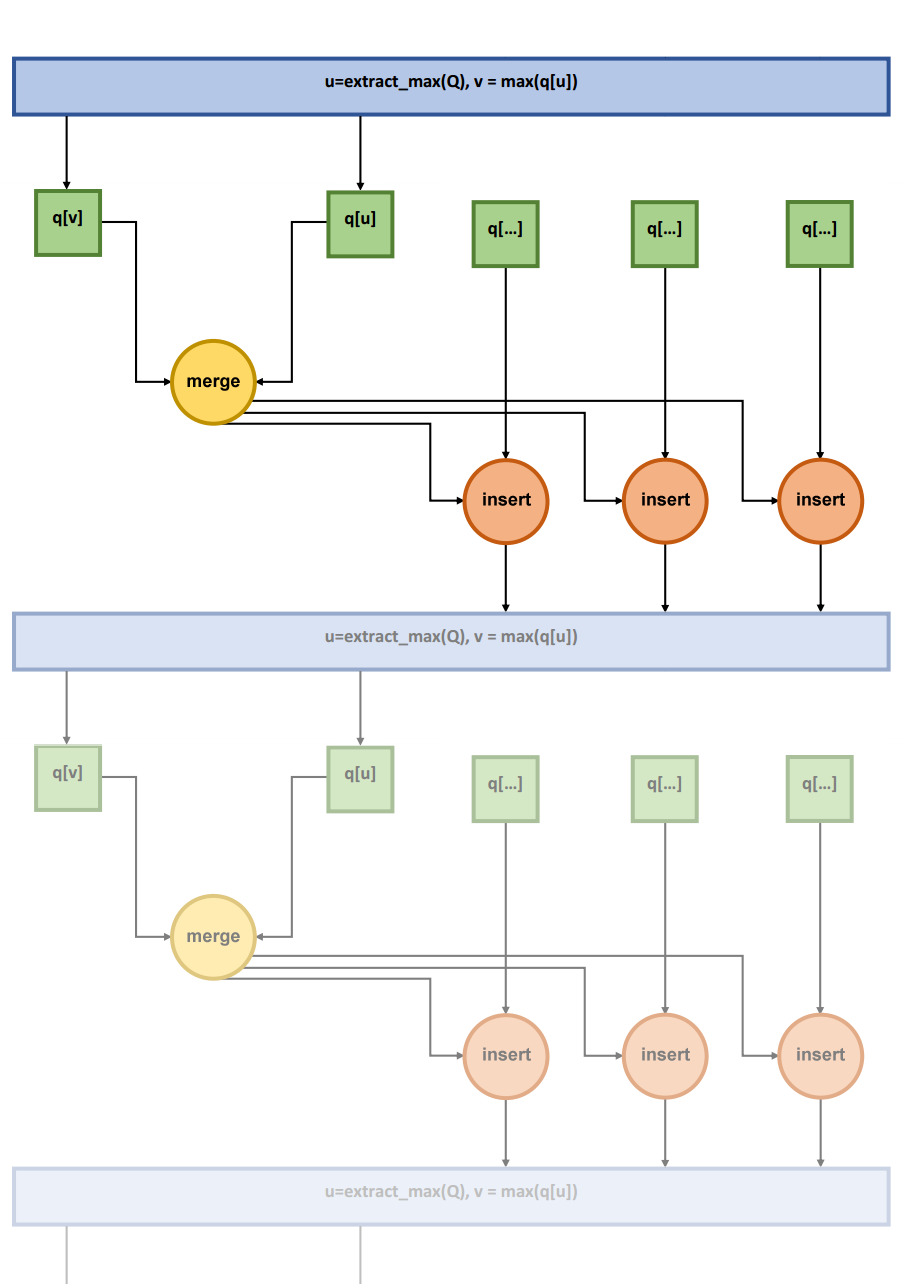
| + | Ниже представлен информационный граф наиболее интересного для рассмотрения этапа алгоритма устойчивой кластеризации с использованием связей - тела цикла (полупрозрачным показана следующая итерация цикла) при <math>n=5</math>. | ||
| + | |||
| + | [[file:rock-graph.png|thumb|center|1000px|Рисунок 1. Граф тела цикла; merge - объединение кластеров, insert - вставка goodness с новым кластером в упорядоченные списки соответствующих кластеров.]] | ||
=== Ресурс параллелизма алгоритма === | === Ресурс параллелизма алгоритма === | ||
| − | ( | + | '''Шаг 1:''' каждая итерация цикла может быть выполнена независимо от всех остальных. Таким образом, в этом случае ширина ЯПФ равна <math>O(M^2)</math>, а высота - <math>O(1)</math>. |
| + | |||
| + | '''Шаг 2:''' при использовании алгоритма наивного перемножения плотных матриц высота ЯПФ равна <math>O(M)</math>, а ширина - <math>O(M^2)</math> (''см. [[Перемножение_плотных_неособенных_матриц_(последовательный_вещественный_вариант)|перемножение плотных матриц]]'') | ||
| + | |||
| + | '''Шаг 3:''' имеет небольшую асимптотическую сложность, может быть выполнен последовательно. | ||
| + | |||
| + | '''Шаг 4:''' имеет небольшую асимптотическую сложность, может быть выполнен последовательно. | ||
| + | |||
| + | '''Шаг 5:''' каждая итерация цикла может быть выполнена только после полного завершения предыдущей, а внутри каждой отдельной итерации все вставки могут быть выполнены независимо друг от друга. Следовательно ширина ЯПФ в этом случае равна <math>O(M)</math>, а высота ЯПФ равна <math>O(MlogM)</math>. | ||
| + | |||
| + | Таким образом, высота ЯПФ зависит от размерности задачи как <math>O(MlogM)</math>, а ширина ЯПФ - как <math>O(M^2)</math>. | ||
=== Входные и выходные данные алгоритма === | === Входные и выходные данные алгоритма === | ||
| − | '''Входные данные''': информация об <math>M</math> | + | '''Входные данные''': информация об <math>M</math> объектах, каждая их которых имеет <math>N</math> бинарных атрибутов. |
| − | '''Объём входных данных''': <math>M \times N</math> бинарных переменных. В силу того, что обычно в большинстве случаев лишь небольшое количество атрибутов | + | '''Объём входных данных''': <math>M \times N</math> бинарных переменных. В силу того, что обычно в большинстве случаев лишь небольшое количество атрибутов объекта имеет значение "true", каждый объект можно хранить в виде списка номеров атрибутов, значения которых равны "true". |
'''Выходные данные''': <math>K</math> кластеров. | '''Выходные данные''': <math>K</math> кластеров. | ||
| − | '''Объём выходных данных''': <math>M</math> индексов | + | '''Объём выходных данных''': <math>M</math> индексов объектов, распределенных в <math>K</math> списков. |
=== Свойства алгоритма === | === Свойства алгоритма === | ||
| − | ( | + | Вычислительная сложность последовательного алгоритма в общем случае равна <math>O(M^{2.37})</math>, а в случае небольшого количества соседних объектов у каждого объекта сложность равна <math>O(M^{2})</math>. |
| + | |||
| + | Вычислительная мощность алгоритма (соотношение количества операций к объему входных и выходных данных) в общем случае равна O(M^{1.37}), в а случае небольшого количества соседних объектов (то есть в том случае, для которого и разрабатывался алгоритм) вычислительная мощность линейна. | ||
| + | |||
| + | Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов, как показано выше, является квадратичным. | ||
== Программная реализация алгоритма == | == Программная реализация алгоритма == | ||
| Строка 171: | Строка 200: | ||
=== Особенности реализации последовательного алгоритма === | === Особенности реализации последовательного алгоритма === | ||
| − | и | + | === Локальность данных и вычислений === |
| + | |||
| + | === Возможные способы и особенности параллельной реализации алгоритма === | ||
| − | === | + | === Масштабируемость алгоритма и его реализации === |
| + | |||
| + | Проведём исследование масштабируемости параллельной реализации алгоритма устройчивой кластеризации с использованием связей, выполненной с использованием OpenMP. Исследование проводилось на персональном компьютере HP Pavilion dv6 (процессор Intel Core i7 3610QM 2300 МГц, 8 логических ядер). | ||
| + | |||
| + | Набор и границы значений изменяемых [[Глоссарий#Параметры запуска|параметров запуска]] реализации алгоритма: | ||
| + | |||
| + | * число нитей [1 : 8] с шагом 1; | ||
| + | * количество точек [500 : 1500] с шагом 100. | ||
| − | + | На следующих рисунках приведены графики времени выполнения выбранной реализации алгоритма устойчивой кластеризации с использованием связей в зависимости от изменяемых параметров запуска. | |
| − | + | [[file:ROCK results 2.png|thumb|center|700px|Рисунок 2. Параллельная реализация алгоритма устойчивой кластеризации с использованием связей. Изменение времени выполнения кластеризации в зависимости от количества точек и от количества параллельных нитей.]] | |
| − | + | Время выполнения кластеризации: | |
| − | = | + | {|border="1" |
| + | | | ||
| + | | 500 объектов | ||
| + | | 1000 объектов | ||
| + | | 1500 объектов | ||
| + | |- | ||
| + | | 1 нить | ||
| + | | 7.930 с | ||
| + | | 63.308 с | ||
| + | | 214.692 с | ||
| + | |- | ||
| + | | 4 нити | ||
| + | | 4.815 с | ||
| + | | 37.275 с | ||
| + | | 126.502 с | ||
| + | |- | ||
| + | | 8 нитей | ||
| + | | 5.312 с | ||
| + | | 39.986 с | ||
| + | | 135.251 с | ||
| + | |} | ||
| − | + | Реализация алгоритма была выполнена автором статьи.<ref>https://gitlab.com/viktorrulev/superprak-1/tree/master</ref> | |
=== Динамические характеристики и эффективность реализации алгоритма === | === Динамические характеристики и эффективность реализации алгоритма === | ||
| − | |||
| − | |||
=== Выводы для классов архитектур === | === Выводы для классов архитектур === | ||
| − | |||
| − | |||
=== Существующие реализации алгоритма === | === Существующие реализации алгоритма === | ||
| − | + | Алгоритм устойчивой кластеризации с иcпользованием связей реализован в пакете CBA языка R.<ref>https://en.wikibooks.org/wiki/Data_Mining_Algorithms_In_R/Clustering/RockCluster</ref> | |
== Литература == | == Литература == | ||
<references \> | <references \> | ||
Текущая версия на 16:06, 3 февраля 2017
 | Эта работа прошла предварительную проверку Дата последней правки страницы: 03.02.2017 Данная работа соответствует формальным критериям. Проверено Teplov. |
| Алгоритм устойчивой кластеризации с иcпользованием связей | |
| Последовательный алгоритм | |
| Последовательная сложность | [math]O(M^2 + M^2m_{nbr} + M^{2}logM)[/math] |
| Объём входных данных | [math]M \times N[/math] |
| Объём выходных данных | [math]M[/math] |
| Параллельный алгоритм | |
| Высота ярусно-параллельной формы | [math]O(MlogM)[/math] |
| Ширина ярусно-параллельной формы | [math]O(M^2)[/math] |
Автор описания: В.А. Рулев.
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Кластеризация (кластерный анализ) — задача разбиения заданной выборки объектов на непересекающиеся подмножества, называемые кластерами, так, чтобы каждый кластер состоял из схожих объектов, а объекты разных кластеров существенно отличались. Каждый объект из выборки характеризуется рядом признаков, которые могут быть вещественными, целочисленными, категорийными (то есть принимающими значения из какого-либо конечного множества), бинарными (принимающими только два значения, обычно [math]true[/math] или [math]false[/math]).
Алгоритм устойчивой кластеризации с иcпользованием связей (robust clustering using links, ROCK) был предложен в 2000 году Sudipto Guha (Stanford University), Rajeev Rastogi (Bell Laboratories) и Kyuseok Shim (Bell Laboratories) [1] для кластеризации объектов с бинарными признаками. При этом алгоритм особенно эффективен, если у каждого объекта лишь небольшое количество признаков имеет значение [math]true[/math].
1.2 Математическое описание алгоритма
В ходе кластеризации [math]M[/math] имеющихся объектов [math]P=\{p_1,...,p_M\}[/math] (каждый объект имеет [math]N[/math] признаков) должны быть разделены на [math]K[/math] непересекающихся подмножеств (кластеров) [math]C_1, ..., C_K[/math] таким образом, чтобы полученные кластеры максимизировали некоторую критериальную функцию [math]E(C_1, ..., C_K)[/math].
Будет называть два объекта [math]p_1[/math] и [math]p_2[/math] соседями, если мера сходства [math]neighbour(p_1,p_2)[/math] этих объектов больше некоторого заранее заданного порогового значения [math]\theta[/math] В качестве меры сходства в алгоритме устойчивой кластеризации с использованием связей используется основанная на коэффициенте Жаккара мера сходства [math]sim(p_1,p_2)[/math]. В ней [math]N(C_i)^{1+2f(\theta)}[/math] имеет смысл ожидаемого (среднего) количества связей внутри одного кластера.
Количеством связей [math]link(p_1,p_2)[/math] между двумя объектами [math]p_1[/math] и [math]p_2[/math] будем называть количество общих соседей этих объектов.
Для того, чтобы сформировать кластеры, удовлетворяющие поставленному условию, необходимо последовательно объединять среди имеющихся кластеров такие пары кластеров, для которых метрика [math]goodness(C_i,C_j)[/math] достигает максимального значения среди всех пар кластеров. На начальном этапе каждый объект считается отдельным кластером.
Формулы метода:
- [math] neighbour(p_1,p_2)=(sim(p_1,p_2)\gt \theta) [/math]
- [math] sim(p_1,p_2)=\frac{N(p_1 \cap p_2)}{N(p_1 \cup p_2)} [/math]
- [math] link(p_1,p_2)=N \Big( \{ p \in P | sim(p_1,p) \lt \theta \} \cap \{ p \in P | sim(p_2,p) \lt \theta \} \Big) [/math]
- [math] E(C_1,...,C_K)=\sum_{i=1}^{K}N(C_i) \ast \sum_{p_q,p_r \in C_i}\frac{link(p_q,p_r)}{N(C_i)^{1+2f(\theta)}} [/math]
- [math] f(\theta)=\frac {1-\theta}{1+\theta} [/math]
- [math] goodness(C_i,C_j)=\frac {\sum_{p_r \in C_i, p_q \in C_j}{link(p_r,p_q)}} {(N(C_i) + N(C_j))^{1+2f(\theta)} - N(C_i)^{1+2f(\theta)} - N(C_j)^{1+2f(\theta)}} [/math]
1.3 Вычислительное ядро алгоритма
Вычислительное ядро алгоритма можно разделить на два основных этапа:
- Вычисление количества связей между каждой парой объектов ([math]\frac {M \times M} {2}[/math] вычислений количества связей)
- Последовательные объединения пар наиболее подходящих кластеров ([math]M-K[/math] поисков пар и объединений)
Подробнее оба этапа будут описаны ниже.
1.4 Макроструктура алгоритма
На макроуровне можно выделить следующие шаги алгоритма:
Шаг 1: вычисление соседних объектов.
Шаг 2: вычисление количества связей между всеми объектами.
Шаг 3: построение для каждого кластера упорядоченного списка значений метрики goodness со всеми остальными кластерами
Шаг 4: построение общего упорядоченного списка значений метрики goodness
Шаг 5 (повторяется то тех пор, пока количество кластеров не достигнет желаемого)
Шаг 5.1: объединение двух кластеров с наилучшим goodness
Шаг 5.2: обновление списков кластеров
1.5 Схема реализации последовательного алгоритма
Ниже приведен псевдокод схемы реализации последовательного алгоритма:
procedure compute_links(P)
begin
for each p[i], p[j] in P do
if sim(p[i], p[j]) > theta
is_neighbour[i, j] = true
else
is_neighbour[i, j] = false
links[i, j] = 0
for each p[i], p[j] in P do
for p[k] in P do
if is_neighbour[i, k] && is_neighbour[j, k]
links[i, j] = links[i, j] + 1
end
procedure cluster(P, k)
begin
links := compute_links(P)
for each p in P do
q[p] := build_local_list(links, p)
Q := build global_list(P, q)
while size(Q) > k do
begin
u := extract_max(Q)
v := extract_max(q[u])
w := merge(u, v)
delete(Q, v)
for each x in (q[u] or q[v]) do
begin
delete(q[x], u);
delete(q[x], v)
insert(q[x], w, goodness(x, w))
insert(q[w], x, goodness(x, w))
update(Q, x, q[x])
end
insert(Q, w, q[w])
deallocate(q[u])
deallocate(q[v])
end
end
1.6 Последовательная сложность алгоритма
Рассмотрим сложности шагов алгоритма из раздела 1.4.
Шаг 1: выполняется с помощью двух вложенных циклов и содержит [math]O(M^2)[/math] операций
Шаг 2: задача сводится к умножению полученной на предыдущем шаге матрицы соседства на саму себя. Это действие быть выполнено с помощью наивного метода за [math]O(M^3)[/math] операций. С помощью алгоритма Копперсмита — Винограда это можно сделать за [math]O(M^{2.37})[/math] операций.[2] В случае, если среднее количество соседей каждого объекта значительно меньше общего количества объектов, связи могут быть вычислены за [math]O(M^2m_{nbr})[/math], где [math]m_{nbr}[/math] - среднее количество соседей объекта.
Шаг 3: имеет сложность [math]O(M)[/math].[3]
Шаг 4: имеет сложность [math]O(M)[/math].
Шаг 5: вычислительная сложность каждой итерации цикла составляет [math]O(MlogM)[/math], так как в худшем случае в ходе итерации выполняется [math]M[/math] вставок элемента в упорядоченный список. Желаемое количество кластеров [math]K[/math] мало по сравнению с [math]M[/math], следовательно можно считать, что нужно выполнить [math]M[/math] итераций цикла. Таким образом, общая вычислительная сложность цикла равна [math]O(M^{2}logM)[/math].
Таким образом, общую последовательную сложность алгоритма в общем случае можно оценить, как
- [math]O(M^2 + M^{2.37} + M^{2}logM)[/math]
или в случае небольшого количества соседних объектов для каждого объекта выборки, как
- [math]O(M^2 + M^2m_{nbr} + M^{2}logM)[/math].
1.7 Информационный граф
Информационный граф перемножения плотных матриц с подробным описанием представлен в статье перемножение плотных матриц
Ниже представлен информационный граф наиболее интересного для рассмотрения этапа алгоритма устойчивой кластеризации с использованием связей - тела цикла (полупрозрачным показана следующая итерация цикла) при [math]n=5[/math].
1.8 Ресурс параллелизма алгоритма
Шаг 1: каждая итерация цикла может быть выполнена независимо от всех остальных. Таким образом, в этом случае ширина ЯПФ равна [math]O(M^2)[/math], а высота - [math]O(1)[/math].
Шаг 2: при использовании алгоритма наивного перемножения плотных матриц высота ЯПФ равна [math]O(M)[/math], а ширина - [math]O(M^2)[/math] (см. перемножение плотных матриц)
Шаг 3: имеет небольшую асимптотическую сложность, может быть выполнен последовательно.
Шаг 4: имеет небольшую асимптотическую сложность, может быть выполнен последовательно.
Шаг 5: каждая итерация цикла может быть выполнена только после полного завершения предыдущей, а внутри каждой отдельной итерации все вставки могут быть выполнены независимо друг от друга. Следовательно ширина ЯПФ в этом случае равна [math]O(M)[/math], а высота ЯПФ равна [math]O(MlogM)[/math].
Таким образом, высота ЯПФ зависит от размерности задачи как [math]O(MlogM)[/math], а ширина ЯПФ - как [math]O(M^2)[/math].
1.9 Входные и выходные данные алгоритма
Входные данные: информация об [math]M[/math] объектах, каждая их которых имеет [math]N[/math] бинарных атрибутов.
Объём входных данных: [math]M \times N[/math] бинарных переменных. В силу того, что обычно в большинстве случаев лишь небольшое количество атрибутов объекта имеет значение "true", каждый объект можно хранить в виде списка номеров атрибутов, значения которых равны "true".
Выходные данные: [math]K[/math] кластеров.
Объём выходных данных: [math]M[/math] индексов объектов, распределенных в [math]K[/math] списков.
1.10 Свойства алгоритма
Вычислительная сложность последовательного алгоритма в общем случае равна [math]O(M^{2.37})[/math], а в случае небольшого количества соседних объектов у каждого объекта сложность равна [math]O(M^{2})[/math].
Вычислительная мощность алгоритма (соотношение количества операций к объему входных и выходных данных) в общем случае равна O(M^{1.37}), в а случае небольшого количества соседних объектов (то есть в том случае, для которого и разрабатывался алгоритм) вычислительная мощность линейна.
Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов, как показано выше, является квадратичным.
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
Проведём исследование масштабируемости параллельной реализации алгоритма устройчивой кластеризации с использованием связей, выполненной с использованием OpenMP. Исследование проводилось на персональном компьютере HP Pavilion dv6 (процессор Intel Core i7 3610QM 2300 МГц, 8 логических ядер).
Набор и границы значений изменяемых параметров запуска реализации алгоритма:
- число нитей [1 : 8] с шагом 1;
- количество точек [500 : 1500] с шагом 100.
На следующих рисунках приведены графики времени выполнения выбранной реализации алгоритма устойчивой кластеризации с использованием связей в зависимости от изменяемых параметров запуска.
Время выполнения кластеризации:
| 500 объектов | 1000 объектов | 1500 объектов | |
| 1 нить | 7.930 с | 63.308 с | 214.692 с |
| 4 нити | 4.815 с | 37.275 с | 126.502 с |
| 8 нитей | 5.312 с | 39.986 с | 135.251 с |
Реализация алгоритма была выполнена автором статьи.[4]
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
Алгоритм устойчивой кластеризации с иcпользованием связей реализован в пакете CBA языка R.[5]
3 Литература
<references \>
- ↑ Sudipto Guha, Rajeev Rastogi, Kyuseok Shim ROCK: A robust clustering algorithm for categorical attributes. 2000. Information Systems. Vol 25, Issue 5, Pages 345-366
- ↑ Donald Coppersmith and Shmuel Winograd. Matrix multiplication via arithmetic progressions. In Proc. of the 19th Annual ACM Symposium on Theory of Computing. 1987.
- ↑ Thomas H. Cormen, Charles E. Leiserson, and Ronald L. Rivest. Introduction to Algorithms. The MIT Press, Massachusetts, 1990.
- ↑ https://gitlab.com/viktorrulev/superprak-1/tree/master
- ↑ https://en.wikibooks.org/wiki/Data_Mining_Algorithms_In_R/Clustering/RockCluster