Двухкубитное преобразование вектора-состояния: различия между версиями
| [непроверенная версия] | [непроверенная версия] |
ASA (обсуждение | вклад) |
ASA (обсуждение | вклад) |
||
| Строка 61: | Строка 61: | ||
=== Информационный граф === | === Информационный граф === | ||
| − | Представим граф алгоритма для случаев <math>n=3, k=1, l=2</math>(рис.1) и <math>n=3, k=1, l=3</math>(рис.2). На графах не представлены матрицы преобразования <math>U,</math> в связи с тем, что их размер при больших <math>n</math> много меньше, нежели размеры входного и выходного векторов. Отметим, что структура графа (а именно обращение к входным данным) сильно зависит от параметров <math>k,l.</math> | + | Представим граф алгоритма для случаев <math>n=3, k=1, l=2</math> (рис.1) и <math>n=3, k=1, l=3</math> (рис.2). На графах не представлены матрицы преобразования <math>U,</math> в связи с тем, что их размер при больших <math>n</math> много меньше, нежели размеры входного и выходного векторов. Отметим, что структура графа (а именно обращение к входным данным) сильно зависит от параметров <math>k,l.</math> |
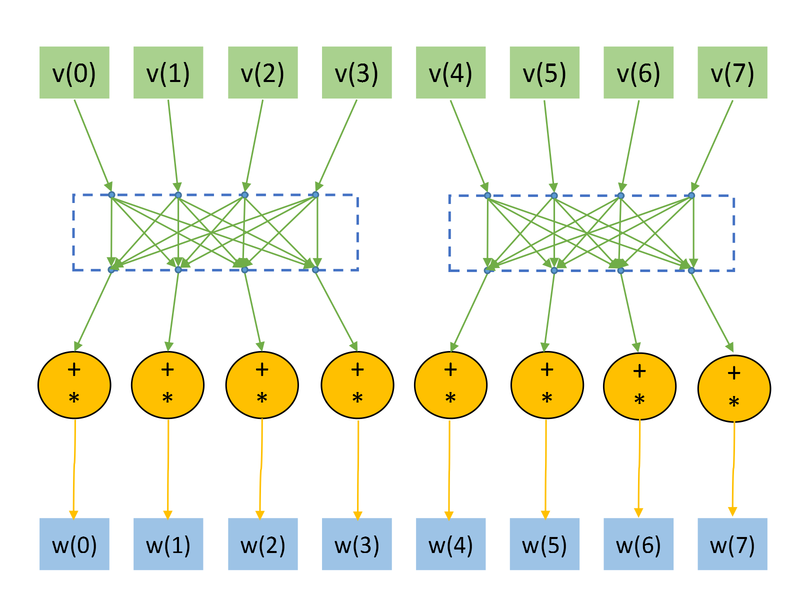
[[file:TwoQubitVectorTransform_23.png|thumb|center|800px|Рисунок 1. Граф алгоритма для <math>n=3, k=2, l=3</math> без отображения матрицы преобразования <math>U.</math> ]] | [[file:TwoQubitVectorTransform_23.png|thumb|center|800px|Рисунок 1. Граф алгоритма для <math>n=3, k=2, l=3</math> без отображения матрицы преобразования <math>U.</math> ]] | ||
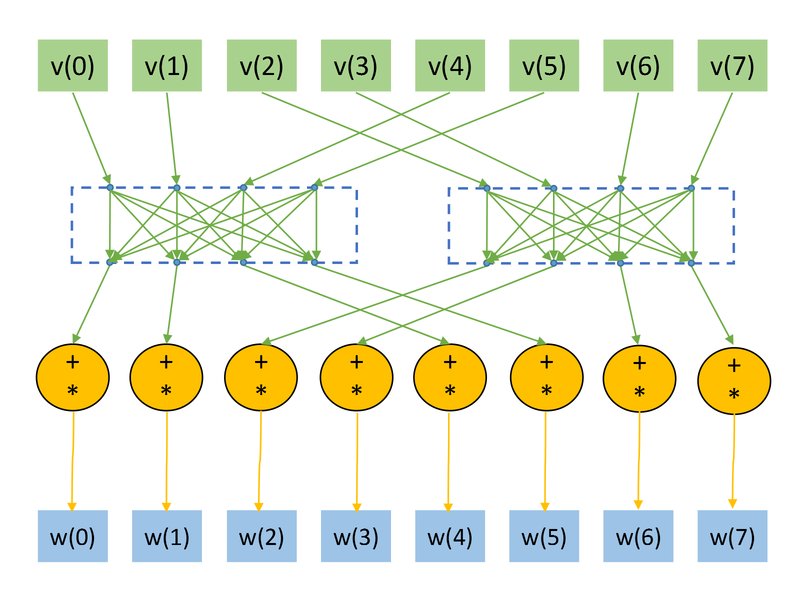
[[file:TwoQubitVectorTransform_13.png|thumb|center|800px|Рисунок 2. Граф алгоритма для <math>n=3, k=1, l=3</math> без отображения матрицы преобразования <math>U.</math> ]] | [[file:TwoQubitVectorTransform_13.png|thumb|center|800px|Рисунок 2. Граф алгоритма для <math>n=3, k=1, l=3</math> без отображения матрицы преобразования <math>U.</math> ]] | ||
Версия 13:51, 29 июля 2015
Основные авторы описания: А.Ю.Чернявский
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Алгоритм производит моделирование действия двухкубитного квантового вентиля на вектор-состояние.
1.2 Математическое описание алгоритма
Исходные данные:
-Целочисленные параметры [math]n - [/math] число кубитов (необязательно) и [math]k,l -[/math] номера кубитов, над которым производится преобразование.
-Комплексная матрица [math]U = {u_{ij}}= \begin{pmatrix} u_{00}^{00} & u_{01}^{00} & u_{10}^{00} & u_{11}^{00}\\ u_{00}^{01} & u_{01}^{01} & u_{10}^{01} & u_{11}^{01}\\ u_{00}^{10} & u_{01}^{10} & u_{10}^{10} & u_{11}^{10}\\ u_{00}^{11} & u_{01}^{11} & u_{10}^{11} & u_{11}^{11} \end{pmatrix}[/math] двухкубитного преобразования размера [math]4 \times 4.[/math] Верхние и нижние двойные индексы обозначают бинарную запись индексов [math]i[/math] и [math]j[/math] (такие обозначения сильно упрощают дальнейшее описание).
-Комплексный вектор [math]v[/math] размерности [math]2^n,[/math] задающей начальное состояние многокубитной системы.
Вычисляемые данные: комплексный вектор [math]w[/math] размерности [math]2^n,[/math] соответствующий состоянию после преобразования.
Формулы метода:
Элементы итогового вектора записываются в следующем виде:
- [math] w_{i_1i_2\ldots i_k \ldots i_l \ldots i_n} = \sum\limits_{j_k=0, j_l=0}^1 u^{j_k j_l}_{i_k i_l} v_{i_1i_2\ldots j_k \ldots j_l \ldots i_n} [/math]
Индекс-кортеж [math]i_1i_2\ldots i_n[/math] представляет собой двоичную запись индекса элемента в массиве.
1.3 Вычислительное ядро алгоритма
Вычислительное ядро алгоритма представляет собой независимое вычисление всех [math]2^n[/math] элементов вектора [math]w.[/math] Вычисление каждого элемента требует четыре операции умножения и три операцию сложения. Кроме того необходимо вычислять индексы типа [math]i_1i_2\ldots j_k \ldots j_l \ldots i_n,[/math] а также значение битов [math]j_k,j_l[/math] что требует побитовых операций.
1.4 Макроструктура алгоритма
Как записано и в описании ядра алгоритма, основную часть метода составляют независимые вычсиления элементов выходного вектора.
1.5 Схема реализации последовательного алгоритма
Для каждого индекса [math]i[/math] от [math]0[/math] до [math]2^n-1[/math]
- Вычислить элементы [math]i_k, i_l[/math] двоичного представления индекса [math]i.[/math]
- Для всех четырех бинарных значений [math]j_k, j_l[/math] вычислить индексы [math]i_1i_2\ldots j_k \ldots j_l \ldots i_n[/math]
- Просуммировать [math]u^{j_k j_l}_{i_k i_l} v_{i_1i_2\ldots j_k \ldots j_l \ldots i_n}.[/math]
1.6 Последовательная сложность алгоритма
Алгоритм требует:
- [math]2^{n+2}[/math] операций умножения комплексных чисел;
- [math]3\dot 2^n[/math] операций сложения комплексных чисел;
- [math]2^{n+1}[/math] операций получения значения [math]k[/math]-го бита числа;
- [math]2^{n+3}[/math] операций изменения значения [math]k[/math]-го бита числа.
Отметим, что данный алгоритм обычно применяется много раз подряд, в связи с чем вычисления, связанные с побитовыми операциями (3-4), могут единожды проводиться в начале алгоритма. Кроме того, от них можно избавиться, пользуясь сложением и логическим умножением с числами [math]2^l,[/math] и [math]2^k,[/math] которые сохраняется для всего алгоритма.
1.7 Информационный граф
Представим граф алгоритма для случаев [math]n=3, k=1, l=2[/math] (рис.1) и [math]n=3, k=1, l=3[/math] (рис.2). На графах не представлены матрицы преобразования [math]U,[/math] в связи с тем, что их размер при больших [math]n[/math] много меньше, нежели размеры входного и выходного векторов. Отметим, что структура графа (а именно обращение к входным данным) сильно зависит от параметров [math]k,l.[/math]