Linpack benchmark: различия между версиями
| [непроверенная версия] | [непроверенная версия] |
Ikramov (обсуждение | вклад) |
Ikramov (обсуждение | вклад) |
||
| Строка 75: | Строка 75: | ||
=== Особенности реализации последовательного алгоритма === | === Особенности реализации последовательного алгоритма === | ||
| − | Строго говоря, при реализации теста испытывающий компьютерную систему испытывает и версии Линпака или другого пакета, откуда он должен вставлять вызовы разложения | + | Строго говоря, при реализации теста испытывающий компьютерную систему испытывает и версии Линпака или другого пакета, откуда он должен вставлять вызовы треугольного разложения матрицы и решения СЛАУ с помощью полученного разложения. Поэтому находящиеся в сети версии теста не являются догмой, поскольку с их помощью можно тестировать и другие версии реализации метода Гаусса. Как уже отмечено выше, из-за того, что треугольное разложение Гаусса вычисляется на месте исходной матрицы, а также из-за того, что при прямом и обратном ходе решение занимает место правой части, после вычисления решения приходится заново перевычислять как матрицу системы, так и правую часть — для последующего вычисления невязки. Это решение вполне можно поменять с целью оптимизации теста. |
=== Локальность данных и вычислений === | === Локальность данных и вычислений === | ||
Версия 10:56, 31 октября 2017
Основные авторы описания: А.В.Фролов, Вад.В.Воеводин (раздел 2.2), А.М.Теплов (раздел 2.4)
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Linpack benchmark является тестом, разработанным как приложение к библиотеке Linpack для тестирования производительности компьютерных систем. По сути это генерирование некоторой системы линейных алгебраических уравнений (СЛАУ) A \vec{x} = \vec{b} со случайной плотной квадратной матрицей A и вектором \vec{b} таким, чтобы решением был вектор \vec{x}, у которого все элементы равны 1, с последующим решением этой СЛАУ. Решение в силу неспецифичности (с рядом оговорок) матрицы делается в несколько этапов. Сначала для матрицы системы выполняется PLU-разложение (P — матрица перестановок, L — левая треугольная с единичными диагональными элементами, U — правая треугольная матрица) методом Гаусса с выбором ведущего элемента по столбцу. На втором этапе с помощью полученного разложения последовательно решается СЛАУ вида P L U \vec{x} = \vec{b}. На третьем этапе вычисляется невязка \vec{r} = A \vec{x} - \vec{b} и её характеристики, после чего выводятся данные о полученных точности и производительности вычислений. Интересно, что производительность вычисляется только для основной части алгоритма, т. е. туда не включены ни вычисление невязки, ни вычисление норм.
Не следует путать Linpack benchmark, разработанный для тестирования компьютеров традиционной архитектуры, и High Performance Linpack benchmark, который разработан для тестирования компьютерных систем с параллельной архитектурой и в основе которого лежит хоть и сходный, но другой алгоритм.
1.2 Математическое описание алгоритма
Исходные данные: невырожденная (ГСЧ подобран так, чтобы это обеспечивалось, в версии от 1992 г.) квадратная матрица A (элементы a_{ij}), вектор правой части \vec{b} (элементы b_i). В реальности они не вполне входные (элементы матрицы генерирует псевдослучайно сама программа, все они находятся в диапазоне (-1/2, +1/2), b_i = \sum\limits_{j = 1}^i a_{ij}), но для разбора общей схемы алгоритма удобно считать их входными данными.
Вычисляемые данные: левая треугольная матрица L (элементы l_{ij}), правая треугольная матрица U (элементы u_{ij}), матрица перестановок P (вычисляется не в развёрнутом виде, а как набор номеров ведущих элементов), вектор решения x (элементы x_i).
Детальные формулы отдельных частей алгоритма здесь описывать не будем, поскольку они являются самостоятельными алгоритмами и их детальные описания должны быть выполнены раздельно. Поэтому здесь будет приведена только общая схема алгоритма.
Первая часть — разложение матрицы в произведение двух треугольных и матрицы перестановок: A = P L U — выполняется методом Гаусса с выбором ведущего элемента по столбцу. При этом матрица перестановок хранится с помощью вектора, характеризующего выполненные перестановки. Матрица L левая треугольная с единичными диагональными элементами, матрица U — правая треугольная.
Вторая часть состоит из двух решений треугольных СЛАУ. Сначала c помощью прямого хода решается система L \vec{y} = P T \vec{b}, затем с помощью обратной подстановки — система U \vec{x} = \vec{y}. При этом в тесте треугольные матрицы хранятся в соответствующих местах матрицы A. Поэтому перед началом третьей части её генерируют заново (с теми же стартовыми параметрами для ГСЧ).
Третья часть (для которой не измеряется скорость работы) состоит в вычислении сначала невязки решения \vec{r} = A \vec{x} - \vec{b} и затем её равномерной нормы, а также нормы решения. По окончании этой части алгоритм выдаёт данные по точности полученного решения, а также вычисляет производительность системы.
1.3 Вычислительное ядро алгоритма
Основная часть алгоритма — разложение матрицы методом Гаусса с выбором ведущих элементов по столбцу — определяет основную часть операций. Следующая по значимости часть — вычисление невязки и её нормы — реализовано подпрограммой вычисления суммы вектора и произведения матрицы на другой вектор и функцией вычисления равномерной нормы. Третьи по значимости части — прямой ход и обратная подстановка в методе Гаусса.
1.4 Макроструктура алгоритма
Как уже записано в описании ядра алгоритма, разложение матрицы методом Гаусса с выбором ведущих элементов по столбцу — определяет основную часть операций и при этом является первой макрооперацией. После неё идёт прямой ход метода Гаусса и сразу за ним обратная подстановка. После повторного заполнения матрицы следующей макрооперацией является вычисление невязки решения СЛАУ, а затем — вычисление её и вектора решения равномерных норм.
1.5 Схема реализации последовательного алгоритма
Математическое описание алгоритма дано выше. При этом в стандартном тесте из-за того, что разложение Гаусса вычисляется на месте исходной матрицы, а также из-за того, что при прямом и обратном ходе решение занимает место правой части, после вычисления решения приходится заново перевычислять как матрицу системы, так и правую часть — для последующего вычисления невязки. После вычисления невязки её норма в принципе может быть вычислена в любом порядке с нормой решения, это не влияет на алгоритм и его результаты.
1.6 Последовательная сложность алгоритма
Поскольку основной частью алгоритма является разложение Гаусса с выбором ведущего элемента по столбцу, то он, как и эта часть, относится к алгоритмам с кубической сложностью. Остальные части квадратичны по сложности и потому не дают сравнимого вклада в сложность алгоритма.
1.7 Информационный граф
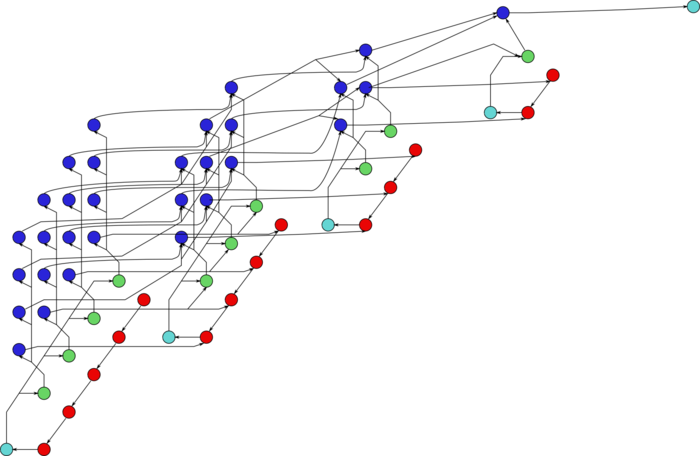
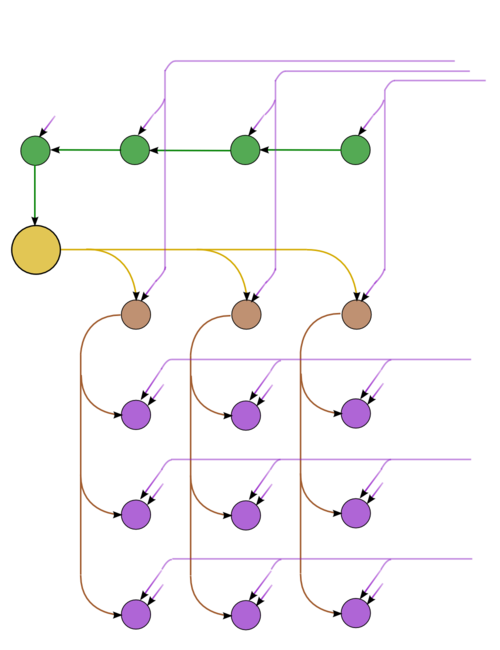
Граф состоит из информационных графов своих основных частей. Первая часть (метод Гаусса с выбором ведущего элемента по столбцу) имеет самый сложный из графов. На рис.1 отражён упрощённый граф этой части, post factum по результатам выборов ведущих элементов. Зеленым отображены операции определения максимумов, с запоминанием позиций. Желтым цветом выделено обращение очередного ведущего элемента, коричневым – умножения в текущем столбце, фиолетовым – операции a b + c в других столбцах. На рис.2 приведён граф одного из слоёв (одного шага метода). Обозначения – те же самые, что в полном графе. Пунктир означает рассылку данных из ведущей строки.
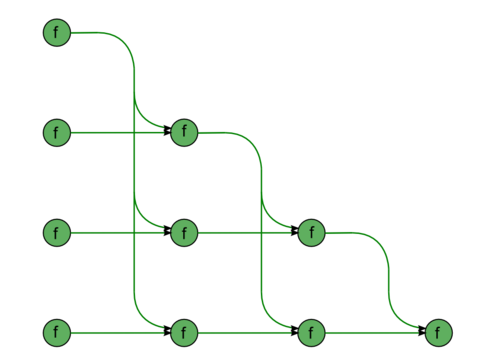
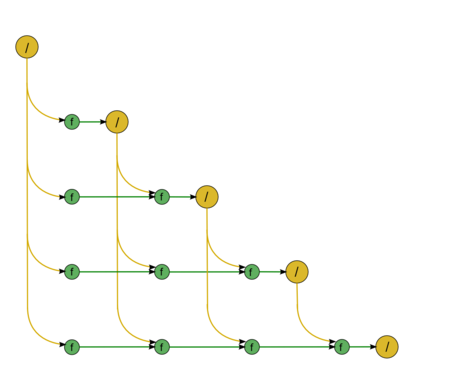
Вторая часть состоит из почти аналогичных фрагментов. Первый из них – «прямой ход», а именно решение СЛАУ с левой треугольной матрицей L \vec{y} = \vec{b} (рис.3). Диагональные элементы матрицы единичны, поэтому в этом куске нет операций деления. Все зелёные вершины отвечают операциям a b + c. Второй – «обратный ход», а именно решение СЛАУ с правой (верхней) треугольной матрицей U \vec{x} = \vec{y} (рис.4). Для её матрицы нет информации о специфичности, и потому в графе появляются также операции деления , они обозначены желтым цветом.
1.8 Ресурс параллелизма алгоритма
При изучении ресурса параллелизма теста видно, что основная сложность (квадратичная) будет у разложения Гаусса с выбором ведущего элемента по столбцу (именно из-за наличия выбора элемента по столбцу). Остальные части алгоритма имеют не более линейной сложности. Поэтому для оптимизации вычислений возможному исследователю нужно заняться именно оптимизацией разложения Гаусса с выбором ведущего элемента по столбцу. Кроме этого, первый кусок второй части (решение первой из треугольных СЛАУ) может быть пристыкован к первой части и исполнен почти полностью «на её фоне», ибо направление перевычисления данных у них совпадают. Однако второй кусок второй части, несмотря на его схожесть с первым, может быть вычислен не ранее, чем будет выполнен весь первый кусок, поскольку у них направления перевычисления данных противоположны.
1.9 Входные и выходные данные алгоритма
По сути теста у него всегда одни и те же данные, причём вычисляемые в самом же тесте. Поэтому в строгом смысле у алгоритма нет входных данных.
Выходными данными являются вычисляемые и выдаваемые тестом нормы невязки, решения, матрицы и их отношения, а также вычисляемая мощность вычислений целевой вычислительной системы.
1.10 Свойства алгоритма
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
Строго говоря, при реализации теста испытывающий компьютерную систему испытывает и версии Линпака или другого пакета, откуда он должен вставлять вызовы треугольного разложения матрицы и решения СЛАУ с помощью полученного разложения. Поэтому находящиеся в сети версии теста не являются догмой, поскольку с их помощью можно тестировать и другие версии реализации метода Гаусса. Как уже отмечено выше, из-за того, что треугольное разложение Гаусса вычисляется на месте исходной матрицы, а также из-за того, что при прямом и обратном ходе решение занимает место правой части, после вычисления решения приходится заново перевычислять как матрицу системы, так и правую часть — для последующего вычисления невязки. Это решение вполне можно поменять с целью оптимизации теста.
2.2 Локальность данных и вычислений
2.2.1 Локальность реализации алгоритма
2.2.1.1 Структура обращений в память и качественная оценка локальности
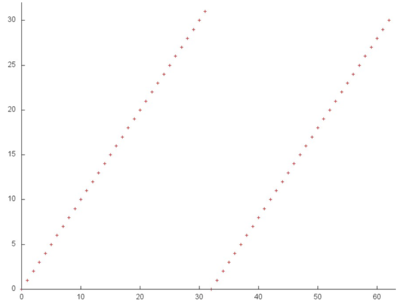
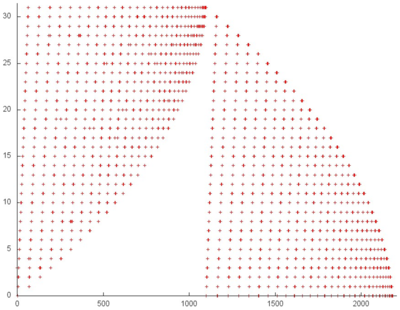
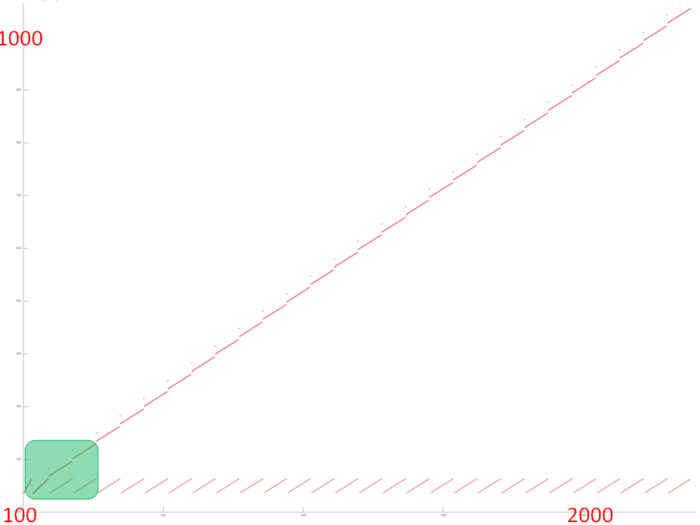
На рис.5 представлен общий профиль обращений в память для теста Linpack. В данном тесте задействовано 3 массива. Обращения к первым двум выделены на рис.5 зеленым цветом (фрагменты 1 и 2), остальные обращения выполняются к элементам третьего массива – матрицы, содержащей коэффициенты СЛАУ. Данный тест состоит из двух этапов – факторизации матрицы и собственно решения СЛАУ. Разделение между этапами отмечено на рисунке оранжевой линией. Видно, что первый этап обладает итерационной структурой, при этом на каждой следующей итерации отбрасываются из рассмотрения несколько элементов матрицы с наименьшими индексами. Также можно заметить, что на втором этапе выполняется два прохода по элементам матрицы с возрастающим шагом, сначала последовательный, затем обратный. Однако в целом профиль устроен достаточно сложно, и для понимания свойств локальности необходимо детальное рассмотрение.
Фрагмент 1 показан отдельно на рис.6. При подобном приближении хорошо видно, что данный фрагмент состоит из двух последовательных переборов всех элементов массива, при этом размер фрагмент очень мал по сравнению с общим профилем. Такой последовательный перебор характеризуется высокой пространственной и достаточно низкой временной локальностью, поскольку к каждому элементу обращение выполняется всего дважды.
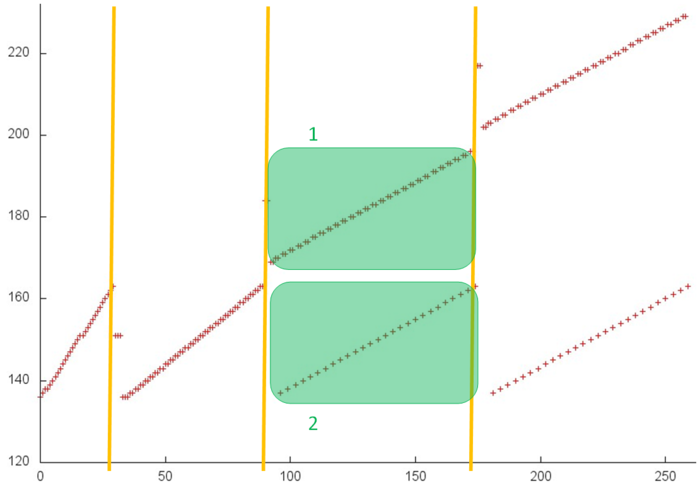
Далее перейдем к рассмотрению фрагмента 2, представленного на рис.7. Данный профиль состоит из двух похожих этапов, состоящих из набора итераций. На каждой итерации выполняется последовательный перебор элементов массива, при этом на следующей итерации отбрасывается их рассмотрения один из элементов: на первом этапе – элемент с минимальным индексом, на втором – с максимальным индексом.
Подобный профиль обладает очень высокой как пространственной, так и временной локальностью, поскольку почти всегда обращения выполняются к соседним элементам, причем элементы достаточно часто используются повторно. Однако заметим, что данный фрагмент состоит всего из около 2000 элементов, что значительно меньше общего числа обращений в программе. Значит, большая часть (и, скорее всего, основное влияние) приходится на последний массив.
На рис.8 представлен фрагмент 3, выделенный на рис.5, соответствующий одной итерации цикла, в котором выполняются обращения к данному массиву. Из данного рисунка хорошо видно, что итерация состоит из двух частей, соответствующих двум внутренним циклам. В обоих случаях число обращений на любой итерации внутреннего цикла примерно равно, однако в первом внутреннем цикле на следующей итерации перебирается следующая часть элементов массива, в то время как во втором цикле перебираются одни и те же элементы.
Остается выяснить структуру обращений в память на итерациях данных двух циклов. Рассмотрим более подробно часть фрагмента, выделенную на рис.8 зеленым (рис.9).
Видно, что первые два этапа отличаются от остальных – на них выполняются некоторые начальные действия. Затем начинаются подобные итерации внутренних циклов, причем в обоих случаях (выделенные зеленым части 1 и 2) выполняется последовательный перебор элементов. Основная разница заключается лишь в том, что в первом цикле обращения к каждому элементу выполняются дважды.
Обращения к данному массиву в рамках внутренних циклов характеризуются высокой пространственной локальностью. При этом во втором цикле используются одни и те же элементы, что приводит также и к достаточно высокой временной локальности. Таким образом, в рамках одной итерации (рис. 4) локальность обращений высока. А при условии, что на разных итерациях происходят обращения к одним и тем же элементам (и число обращений на каждой итерации не так уж велико), это приводит к дальнейшему повышению локальности.
2.2.1.2 Количественная оценка локальности
Основной фрагмент реализации, на основе которого были получены количественные оценки, приведен здесь (оригинал исходного кода взят отсюда). Условия запуска описаны здесь.
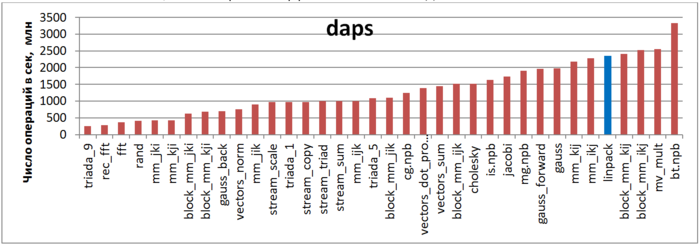
Первая оценка выполняется на основе характеристики daps, которая оценивает число выполненных обращений (чтений и записей) в память в секунду. Данная характеристика является аналогом оценки flops применительно к работе с памятью и является в большей степени оценкой производительности взаимодействия с памятью, чем оценкой локальности. Однако она служит хорошим источником информации, в том числе для сравнения с результатами по следующей характеристике cvg.
На рис.10 приведены значения daps для реализаций распространенных алгоритмов, отсортированные по возрастанию (чем больше daps, тем в общем случае выше производительность). Можно увидеть, что данный показатель у теста Linpack один из самых высоких, что говорит об эффективном взаимодействии с памятью.
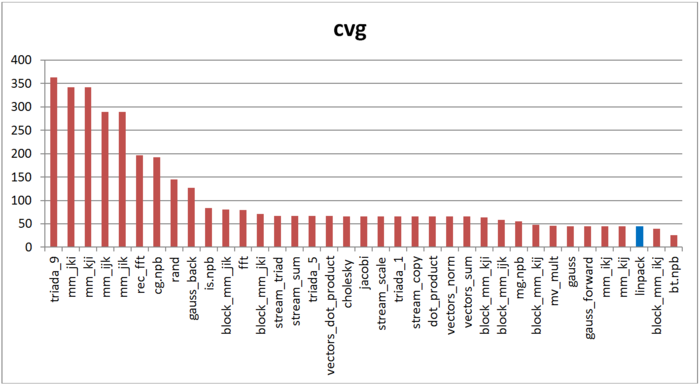
Вторая характеристика – cvg – предназначена для получения более машинно-независимой оценки локальности. Она определяет, насколько часто в программе необходимо подтягивать данные в кэш-память. Соответственно, чем меньше значение cvg, тем реже это нужно делать, тем лучше локальность.
На рис.11 приведены значения cvg для того же набора реализаций, отсортированные по убыванию (чем меньше cvg, тем в общем случае выше локальность). Можно увидеть, что, согласно данной оценке, локальность обращений в память теста Linpack очень высока, что соответствует полученным ранее оценкам и выводам.
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
2.4.1 Масштабируемость алгоритма
2.4.2 Масштабируемость реализации алгоритма
Проведём исследование масштабируемости реализации HPL теста Linpack согласно методике. Исследование проводилось на суперкомпьютере "Ломоносов" Суперкомпьютерного комплекса Московского университета.
Набор и границы значений изменяемых параметров запуска реализации алгоритма:
- число процессоров [8 : 128] с шагом 8;
- размер матрицы [1000 : 100000] c шагом 1000.
В результате проведённых экспериментов был получен следующий диапазон эффективности реализации алгоритма:
- минимальная эффективность реализации 0.039%;
- максимальная эффективность реализации 86,7%.
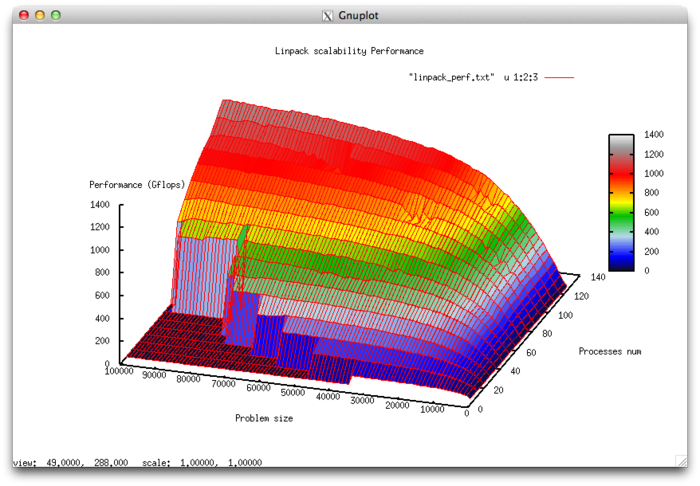
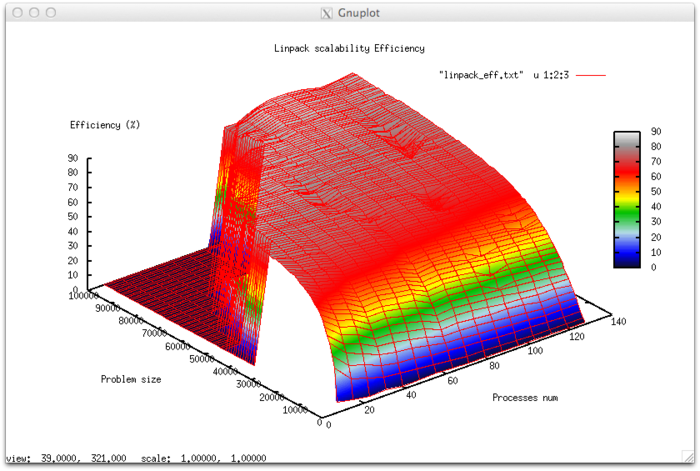
На следующих рисунках приведены графики производительности и эффективности теста HPL в зависимости от изменяемых параметров запуска.
Построим оценки масштабируемости теста Linpack:
- По числу процессов: -0.061256. При увеличении числа процессов эффективность на рассмотренной области изменений параметров запуска уменьшается, однако в целом уменьшение не очень быстрое. Малая интенсивность изменения объясняется высокой общей эффективностью работы при больших размерах задачи, однако при росте числа процессов эффективность равномерно уменьшается. Это объясняется также тем, что с ростом вычислительной сложности падение эффективности становится не таким быстрым. Уменьшение эффективности на рассмотренной области работы параллельной программы объясняется быстрым ростом накладных расходов на организацию параллельного выполнения. С ростом вычислительной сложности задачи эффективность снижается так же быстро, но при больших значениях числа процессов. Это подтверждает предположение о том, что накладные расходы начинают сильно превалировать над вычислениями.
- По размеру задачи: 0.010134. При увеличении размера задачи эффективность возрастает. Эффективность возрастает тем быстрее, чем большее число процессов используется для выполнения. Это подтверждает предположение о том, что размер задачи сильно влияет на эффективность выполнения приложения. Оценка показывает, что с ростом размера задачи эффективность на рассмотренной области значений параметров запуска сильно увеличивается. Также, учитывая разницу максимальной и минимальной эффективности почти в 80%, можно сделать вывод, что рост эффективности при увеличении размера задачи наблюдается на большей части рассмотренной области значений.
- По двум направлениям: 0.0000284 При рассмотрении увеличения как вычислительной сложности, так и числа процессов на всей рассмотренной области значений эффективность увеличивается, однако скорость увеличения эффективности не очень большая.
Исследованная реализация теста