Алгоритм Дейкстры: различия между версиями
| [непроверенная версия] | [досмотренная версия] |
Daryin (обсуждение | вклад) |
ASA (обсуждение | вклад) |
||
| (не показано 38 промежуточных версий 8 участников) | |||
| Строка 1: | Строка 1: | ||
| − | == Свойства и структура | + | {{level-a}} |
| + | Основные авторы описания: [[Участник:Daryin|А.Н.Дарьин]] | ||
| + | |||
| + | == Свойства и структура алгоритма == | ||
=== Общее описание алгоритма === | === Общее описание алгоритма === | ||
| Строка 5: | Строка 8: | ||
Алгоритм Дейкстры (с использованием фибоначчиевой кучи<ref name=FibHeap>Fredman, Michael L, and Robert Endre Tarjan. “Fibonacci Heaps and Their Uses in Improved Network Optimization Algorithms.” Journal of the ACM 34, no. 3 (July 1987): 596–615. doi:10.1145/28869.28874.</ref>) выполняется за время <math>O(m + n \ln n)</math> и является асимптотически быстрейшим из известных последовательных алгоритмов для данного класса задач. | Алгоритм Дейкстры (с использованием фибоначчиевой кучи<ref name=FibHeap>Fredman, Michael L, and Robert Endre Tarjan. “Fibonacci Heaps and Their Uses in Improved Network Optimization Algorithms.” Journal of the ACM 34, no. 3 (July 1987): 596–615. doi:10.1145/28869.28874.</ref>) выполняется за время <math>O(m + n \ln n)</math> и является асимптотически быстрейшим из известных последовательных алгоритмов для данного класса задач. | ||
| − | === Математическое описание === | + | === Математическое описание алгоритма === |
| + | |||
| + | Пусть задан граф <math>G = (V, E)</math> с весами рёбер <math>f(e)</math> и выделенной вершиной-источником <math>u</math>. Обозначим через <math>d(v)</math> кратчайшее расстояние от источника <math>u</math> до вершины <math>v</math>. | ||
| + | |||
| + | Пусть уже вычислены все расстояния, не превосходящие некоторого числа <math>r</math>, то есть расстояния до вершин из множества <math>V_r = \{ v \in V \mid d(v) \le r \}</math>. Пусть | ||
| + | :<math> | ||
| + | (v, w) \in \arg\min \{ d(v) + f(e) \mid v \in V, e = (v, w) \in E \}. | ||
| + | </math> | ||
| + | Тогда <math>d(w) = d(v) + f(e)</math>, и <math>v</math> лежит на кратчайшем пути от <math>u</math> к <math>w</math>. | ||
| + | |||
| + | Величины <math>d^+(w) = d(v) + f(e)</math>, где <math>v \in V_r</math>, <math>e = (v, w) \in E</math>, называются ''предполагаемыми расстояниями'' и являются оценкой сверху для настоящих расстояний: <math>d(w) \le d^+(w)</math>. | ||
| + | |||
| + | Алгоритм Дейкстры на каждом шаге находит вершину с наименьшим предполагаемым расстоянием, помечает её как посещённую и обновляет предполагаемые расстояния для всех концов рёбер, исходящих из неё. | ||
| + | |||
=== Вычислительное ядро алгоритма === | === Вычислительное ядро алгоритма === | ||
| + | Основные вычисления связаны с операциями над очередью с приоритетом: | ||
| + | * извлечение минимального элемента (<code>delete_min</code>); | ||
| + | * уменьшение приоритета элемента (<code>decrease_key</code>). | ||
| + | |||
=== Макроструктура алгоритма === | === Макроструктура алгоритма === | ||
| − | === | + | Псевдокод алгоритма: |
| + | |||
| + | '''Входные данные''': | ||
| + | граф с вершинами ''V'', рёбрами ''E'' с весами ''f''(''e''); | ||
| + | вершина-источник ''u''. | ||
| + | '''Выходные данные''': расстояния ''d''(''v'') до каждой вершины ''v'' ∈ ''V'' от вершины ''u''. | ||
| + | |||
| + | ''Q'' := '''new''' priority queue | ||
| + | '''for each''' ''v'' ∈ ''V'': | ||
| + | '''if''' ''v'' = ''u'' '''then''' ''d''(''v'') := 0 '''else''' ''d''(''v'') := ∞ | ||
| + | ''Q''.insert(''v'', ''d''(''v'')) | ||
| + | |||
| + | '''while''' ''Q'' ≠ ∅: | ||
| + | ''v'' := ''Q''.delete_min() | ||
| + | '''for each''' ''e'' = (''v'', ''w'') ∈ ''E'': | ||
| + | '''if''' ''d''(''w'') > ''d''(''v'') + ''f''(''e''): | ||
| + | ''d''(''w'') := ''d''(''v'') + ''f''(''e'') | ||
| + | ''Q''.decrease_key(''w'', ''d''(''w'')) | ||
| + | |||
| + | === Схема реализации последовательного алгоритма === | ||
| + | Конкретная реализация алгоритма Дейкстры определяется выбором используемого алгоритма очереди с приоритетом. В простейшем случае это может быть массив или список, поиск минимума в котором требует просмотра всех вершин. Более эффективным является использование кучи; наилучшую известную оценку сложности имеет вариант с использованием фибоначчиевой кучи<ref name=FibHeap />. | ||
| + | |||
| + | Возможен вариант реализации, когда вершины добавляются в очередь не на этапе инициализации, а в момент первого посещения. | ||
| + | |||
=== Последовательная сложность алгоритма === | === Последовательная сложность алгоритма === | ||
| Строка 20: | Строка 63: | ||
=== Информационный граф === | === Информационный граф === | ||
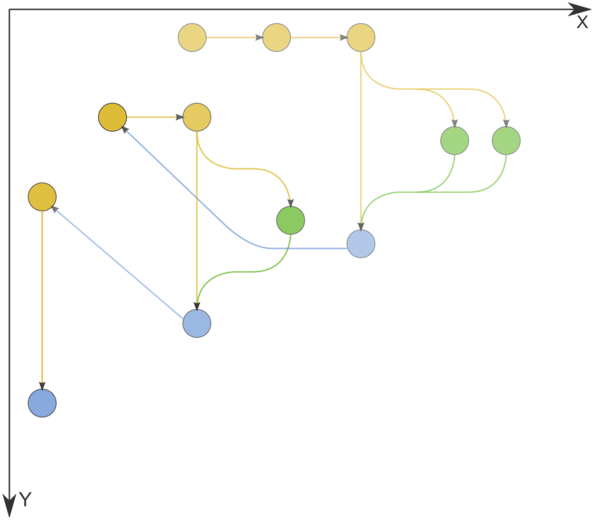
| − | === | + | Приводится граф алгоритма для базовой реализации алгоритма Дейкстры на списках или массивах. |
| + | [[file:Deikstra.png|thumb|center|600px|Рисунок 1. Граф алгоритма без отображения входных и выходных данных. n=3. Желтым цветом обозначены операции сравнения, зеленым - операции изменения меток вершин, синим - пометка вершины.]] | ||
| + | |||
| + | === Ресурс параллелизма алгоритма === | ||
Алгоритм Дейкстры допускает эффективную параллелизацию<ref>Crauser, A, K Mehlhorn, U Meyer, and P Sanders. “A Parallelization of Dijkstra's Shortest Path Algorithm,” Proceedings of Mathematical Foundations of Computer Science / Lecture Notes in Computer Science, 1450:722–31, Berlin, Heidelberg: Springer, 1998. doi:10.1007/BFb0055823.</ref>, среднее время работы <math>O(n^{1/3}\ln n)</math> с объёмом вычислений <math>O(n \ln n + m)</math>. | Алгоритм Дейкстры допускает эффективную параллелизацию<ref>Crauser, A, K Mehlhorn, U Meyer, and P Sanders. “A Parallelization of Dijkstra's Shortest Path Algorithm,” Proceedings of Mathematical Foundations of Computer Science / Lecture Notes in Computer Science, 1450:722–31, Berlin, Heidelberg: Springer, 1998. doi:10.1007/BFb0055823.</ref>, среднее время работы <math>O(n^{1/3}\ln n)</math> с объёмом вычислений <math>O(n \ln n + m)</math>. | ||
| Строка 26: | Строка 72: | ||
[[Алгоритм Δ-шагания]] может рассматриваться как параллельная версия алгоритма Дейкстры. | [[Алгоритм Δ-шагания]] может рассматриваться как параллельная версия алгоритма Дейкстры. | ||
| − | === | + | === Входные и выходные данные алгоритма === |
| − | === Свойства алгоритма=== | + | '''Входные данные''': взвешенный граф <math>(V, E, W)</math> (<math>n</math> вершин <math>v_i</math> и <math>m</math> рёбер <math>e_j = (v^{(1)}_{j}, v^{(2)}_{j})</math> с весами <math>f_j</math>), вершина-источник <math>u</math>. |
| − | == Программная реализация | + | |
| + | '''Объём входных данных''': <math>O(m + n)</math>. | ||
| + | |||
| + | '''Выходные данные''' (возможные варианты): | ||
| + | # для каждой вершины <math>v</math> исходного графа – последнее ребро <math>e^*_v = (w, v)</math>, лежащее на кратчайшем пути от вершины <math>u</math> к <math>v</math>, или соответствующая вершина <math>w</math>; | ||
| + | # для каждой вершины <math>v</math> исходного графа – суммарный вес <math>f^*(v)</math> кратчайшего пути от вершины <math>u</math> к <math>v</math>. | ||
| + | |||
| + | '''Объём выходных данных''': <math>O(n)</math>. | ||
| + | |||
| + | === Свойства алгоритма === | ||
| + | |||
| + | == Программная реализация алгоритма == | ||
=== Особенности реализации последовательного алгоритма === | === Особенности реализации последовательного алгоритма === | ||
| − | + | ||
| − | === Возможные способы и особенности реализации | + | === Возможные способы и особенности параллельной реализации алгоритма === |
| − | + | === Результаты прогонов === | |
| − | === | ||
=== Выводы для классов архитектур === | === Выводы для классов архитектур === | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== Литература == | == Литература == | ||
<references /> | <references /> | ||
| + | |||
| + | [[Категория:Статьи в работе]] | ||
| + | |||
| + | [[En:Dijkstra's algorithm]] | ||
Текущая версия на 15:00, 4 июля 2022
Основные авторы описания: А.Н.Дарьин
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Алгоритм Дейкстры[1] предназначен для решения задачи поиска кратчайшего пути на графе. Для заданного ориентированного взвешенного графа с неотрицательными весами алгоритм находит кратчайшие расстояния от выделенной вершины-источника до всех остальных вершин графа. Алгоритм Дейкстры (с использованием фибоначчиевой кучи[2]) выполняется за время [math]O(m + n \ln n)[/math] и является асимптотически быстрейшим из известных последовательных алгоритмов для данного класса задач.
1.2 Математическое описание алгоритма
Пусть задан граф [math]G = (V, E)[/math] с весами рёбер [math]f(e)[/math] и выделенной вершиной-источником [math]u[/math]. Обозначим через [math]d(v)[/math] кратчайшее расстояние от источника [math]u[/math] до вершины [math]v[/math].
Пусть уже вычислены все расстояния, не превосходящие некоторого числа [math]r[/math], то есть расстояния до вершин из множества [math]V_r = \{ v \in V \mid d(v) \le r \}[/math]. Пусть
- [math] (v, w) \in \arg\min \{ d(v) + f(e) \mid v \in V, e = (v, w) \in E \}. [/math]
Тогда [math]d(w) = d(v) + f(e)[/math], и [math]v[/math] лежит на кратчайшем пути от [math]u[/math] к [math]w[/math].
Величины [math]d^+(w) = d(v) + f(e)[/math], где [math]v \in V_r[/math], [math]e = (v, w) \in E[/math], называются предполагаемыми расстояниями и являются оценкой сверху для настоящих расстояний: [math]d(w) \le d^+(w)[/math].
Алгоритм Дейкстры на каждом шаге находит вершину с наименьшим предполагаемым расстоянием, помечает её как посещённую и обновляет предполагаемые расстояния для всех концов рёбер, исходящих из неё.
1.3 Вычислительное ядро алгоритма
Основные вычисления связаны с операциями над очередью с приоритетом:
- извлечение минимального элемента (
delete_min); - уменьшение приоритета элемента (
decrease_key).
1.4 Макроструктура алгоритма
Псевдокод алгоритма:
Входные данные:
граф с вершинами V, рёбрами E с весами f(e);
вершина-источник u.
Выходные данные: расстояния d(v) до каждой вершины v ∈ V от вершины u.
Q := new priority queue
for each v ∈ V:
if v = u then d(v) := 0 else d(v) := ∞
Q.insert(v, d(v))
while Q ≠ ∅:
v := Q.delete_min()
for each e = (v, w) ∈ E:
if d(w) > d(v) + f(e):
d(w) := d(v) + f(e)
Q.decrease_key(w, d(w))
1.5 Схема реализации последовательного алгоритма
Конкретная реализация алгоритма Дейкстры определяется выбором используемого алгоритма очереди с приоритетом. В простейшем случае это может быть массив или список, поиск минимума в котором требует просмотра всех вершин. Более эффективным является использование кучи; наилучшую известную оценку сложности имеет вариант с использованием фибоначчиевой кучи[2].
Возможен вариант реализации, когда вершины добавляются в очередь не на этапе инициализации, а в момент первого посещения.
1.6 Последовательная сложность алгоритма
Последовательная сложность алгоритма равна [math]O(C_1 m + C_2n)[/math], где
- [math]C_1[/math] – количество операций уменьшения расстояния до вершины;
- [math]C_2[/math] – количество операций вычисления минимума.
Оригинальный алгоритм Дейкстры использовал в качестве внутренней структуры данных списки, для которых [math]C_1 = O(1)[/math], [math]C_2 = O(n)[/math], так что общая сложность составляла [math]O(n^2)[/math].
При использовании фибоначчиевой кучи[2] время вычисления минимума сокращается до [math]C_2 = O(\ln n)[/math], так что общая сложность равна [math]O(m + n \ln n)[/math], что является асимптотически наилучшим известным результатом для данного класса задач.
1.7 Информационный граф
Приводится граф алгоритма для базовой реализации алгоритма Дейкстры на списках или массивах.
1.8 Ресурс параллелизма алгоритма
Алгоритм Дейкстры допускает эффективную параллелизацию[3], среднее время работы [math]O(n^{1/3}\ln n)[/math] с объёмом вычислений [math]O(n \ln n + m)[/math].
Алгоритм Δ-шагания может рассматриваться как параллельная версия алгоритма Дейкстры.
1.9 Входные и выходные данные алгоритма
Входные данные: взвешенный граф [math](V, E, W)[/math] ([math]n[/math] вершин [math]v_i[/math] и [math]m[/math] рёбер [math]e_j = (v^{(1)}_{j}, v^{(2)}_{j})[/math] с весами [math]f_j[/math]), вершина-источник [math]u[/math].
Объём входных данных: [math]O(m + n)[/math].
Выходные данные (возможные варианты):
- для каждой вершины [math]v[/math] исходного графа – последнее ребро [math]e^*_v = (w, v)[/math], лежащее на кратчайшем пути от вершины [math]u[/math] к [math]v[/math], или соответствующая вершина [math]w[/math];
- для каждой вершины [math]v[/math] исходного графа – суммарный вес [math]f^*(v)[/math] кратчайшего пути от вершины [math]u[/math] к [math]v[/math].
Объём выходных данных: [math]O(n)[/math].
1.10 Свойства алгоритма
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Возможные способы и особенности параллельной реализации алгоритма
2.3 Результаты прогонов
2.4 Выводы для классов архитектур
3 Литература
- ↑ Dijkstra, E W. “A Note on Two Problems in Connexion with Graphs.” Numerische Mathematik 1, no. 1 (December 1959): 269–71. doi:10.1007/BF01386390.
- ↑ 2,0 2,1 2,2 Fredman, Michael L, and Robert Endre Tarjan. “Fibonacci Heaps and Their Uses in Improved Network Optimization Algorithms.” Journal of the ACM 34, no. 3 (July 1987): 596–615. doi:10.1145/28869.28874.
- ↑ Crauser, A, K Mehlhorn, U Meyer, and P Sanders. “A Parallelization of Dijkstra's Shortest Path Algorithm,” Proceedings of Mathematical Foundations of Computer Science / Lecture Notes in Computer Science, 1450:722–31, Berlin, Heidelberg: Springer, 1998. doi:10.1007/BFb0055823.