Участник:Vika3410/Метод Разделяй и властвуй: различия между версиями
Vika3410 (обсуждение | вклад) |
IgorS (обсуждение | вклад) |
||
| (не показано 113 промежуточных версий 5 участников) | |||
| Строка 1: | Строка 1: | ||
| − | \ | + | {{Assignment|IgorS}} |
| + | |||
| + | Авторы статьи: [[Участник:NikoSergAlex|Сергеев Никита]] (группа 614) (1.1, 1.2, 1.5, 1.6, 1.7, 1.8, 1.10, 2.4), [[Участница:Vika3410|Стрельцова Виктория]] (группа 614) (1.2, 1.3, 1.4, 1.6, 1.7, 1.9, 1.10, 2.4) | ||
| + | {{algorithm | ||
| + | | name = Метод "Разделяй и властвуй" вычисления собственных значений и векторов трёхдиагональной матрицы | ||
| + | | serial_complexity = <math> c\frac{4}{3}n^{3} </math> | ||
| + | | parallel_complexity = <math> O(n^{2.3}) </math> | ||
| + | |||
| + | крайне редко: <math> O(n^{2}) </math> | ||
| + | | pf_width = | ||
| + | | input_data = <math> 2n + 1 </math> | ||
| + | | output_data = <math> n(n + 1) </math> | ||
| + | }} | ||
| + | |||
| + | = Свойства и структура алгоритма = | ||
| − | |||
== Общее описание алгоритма == | == Общее описание алгоритма == | ||
| − | '''Метод разделяй и властвуй вычисления собственных значений и векторов трёхдиагональной матрицы''' - | + | '''Метод разделяй и властвуй вычисления собственных значений и векторов трёхдиагональной матрицы''' - является наиболее быстрым из существующих методов вычисления всех собственных значений и собственных векторов трехдиагональной матрицы, начиная с порядка n, который примерно равен 26. (Точное значение этого порогового порядка в конкретном случае зависит от компьютера.) |
| + | |||
| + | Численно устойчивая реализация данного метода весьма не тривиальна, так как не смотря на то, что впервые метод был предложен в 1981 г., "правильный" способ реализации метода был найден лишь в 1992 г. Этот способ был воплощен при помощи LAPACK-программ ssyevd (для плотных матриц) и sstevd (для трехдиагональных матриц). В этих программах стратегия "разделяй-и-влавствуй" используется для матриц порядка выше 25. | ||
| + | |||
| + | Для матриц порядка ниже 25 (или в тех случаях, когда требуются только собственные значения) автоматически происходит переход к методу QR-итерации. | ||
== Математическое описание алгоритма == | == Математическое описание алгоритма == | ||
| Строка 47: | Строка 64: | ||
</math> | </math> | ||
| − | + | В предположении, что известны спектральные разложения матриц <math>T_{1}</math> и <math>T_{2}</math>: | |
| − | <math>T_{i}=Q_{i} \Lambda_{i} Q_{i}^{T} </math>. | + | <math>T_{i}=Q_{i} \Lambda_{i} Q_{i}^{T} </math>. На самом деле, они будут вычисляться рекурсивно тем же самым алгоритмом. |
| − | + | Можно установить связь между собственными значениями матрицы Т и собственными значениями матриц | |
| − | <math>T_{1}</math> и <math>T_{2}</math>. | + | <math>T_{1}</math> и <math>T_{2}</math>. Получается: |
<math> | <math> | ||
| Строка 59: | Строка 76: | ||
</math>, | </math>, | ||
| − | где <math> u = \begin{bmatrix} Q_{1}^{T} & 0 \\ 0 & Q_{2}^{T}\end{bmatrix} v </math>, | + | где <math> u = \begin{bmatrix} Q_{1}^{T} & 0 \\ 0 & Q_{2}^{T}\end{bmatrix} v </math> - матрица, в первой строке которой находятся элементы последнего столбца матрицы <math> Q_{1}^{T}</math>, а во второй - элементы первого столбца матрицы <math> Q_{2}^{T}</math>, так как <math>v = \begin{bmatrix} 0 , \ldots , 0 , 1 , 1 , 0 \ldots , 0 \end{bmatrix} ^T</math>. |
| − | + | Следовательно, <math>T</math> имеет такие же собственные значения, что и подобная ей матрица <math>D + \rho uu^{T}</math>, | |
| − | так как <math>v = \begin{bmatrix} 0 , \ldots , 0 , 1 , 1 , 0 \ldots , 0 \end{bmatrix} ^T | ||
| − | |||
| − | Следовательно, <math>T</math> имеет | ||
где <math>D = \begin{bmatrix} L_{1} & 0 \\ 0 & L_{2}\end{bmatrix} </math> - диагональная матрица, | где <math>D = \begin{bmatrix} L_{1} & 0 \\ 0 & L_{2}\end{bmatrix} </math> - диагональная матрица, | ||
<math>\rho = b_{m}</math> - число, а <math>u</math> - вектор. | <math>\rho = b_{m}</math> - число, а <math>u</math> - вектор. | ||
| + | В дальнейшем предполагаем, не ограничивая общности, что диагональные элементы <math>d_{1}, \ldots, d_{n}</math> матрицы <math>D</math> упорядочены по не возрастанию: <math>d_{n} <= \ldots <=d_{1}</math>. | ||
| − | + | Для того, чтобы найти собственные значения матрицы <math>D + \rho uu^{T}</math>, потребуется вычислить её характеристический многочлен, считая пока матрицу <math>D - \lambda I</math> невырожденной. | |
| − | + | Тогда получаем | |
| − | + | <math>det(D + \rho uu^{T} - \lambda I) = det((D - \lambda I)(I + \rho (D- \lambda I)^{-1} uu^{T}))</math>. | |
| − | |||
| − | + | Так как <math>D - \lambda I</math> невырожденная, <math>det(I + \rho (D - \lambda I)^{-1}uu^{T}) = 0</math> тогда и только тогда, когда <math>\lambda</math> - является собственным значением. Можем заметить, что матрица <math>I + \rho (D - \lambda I)^{-1}uu^{T}</math> получается из единичной путём добавления матрицы ранга 1. Определитель такой матрицы не сложно вычислить. | |
| − | + | ''Лемма 1.'' Справедливо равенство <math>det(I + xy^{T}) = 1 + y^{T}x</math>, где <math>x</math> и <math>y</math> - векторы. | |
| − | + | Следовательно, получаем | |
| + | <math>det(I + \rho (D - \lambda I)^{-1}uu^{T}) = 1 + \rho u^{T}(D - \lambda I)^{-1}u</math> <math> = 1 + \rho \sum_{i=1, n} \frac{u_{i}^{2}} {d_{i}-\lambda} \equiv f(\lambda)</math> , | ||
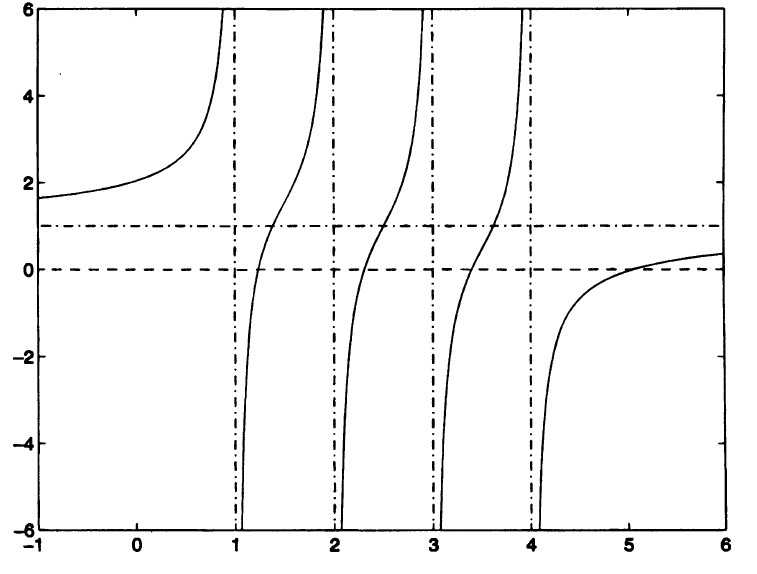
| − | + | т.е. собственные значения матрицы <math>T</math> являются корнями так называемого векового уравнения <math>f(\lambda) = 0</math>. Если все числа <math>d_{i}</math> различны между собой и все <math>u_{i} <> 0</math> (случай общего положения), то <math>f(\lambda)</math> имеет график типа, который показан на рис.1(где <math>n = 4</math> и <math>\rho > 0</math>). | |
| − | |||
| − | |||
| − | |||
| − | т.е. собственные значения матрицы <math>T</math> | ||
[[File:Сергеев 1.jpg|thumb|center|800px|Рис. 1. График функции <math> f(\lambda) = 1 + \frac{0.5}{1 - \lambda} + \frac{0.5}{2 - \lambda} + \frac{0.5}{3 - \lambda} + \frac{0.5}{4 - \lambda}</math>]] | [[File:Сергеев 1.jpg|thumb|center|800px|Рис. 1. График функции <math> f(\lambda) = 1 + \frac{0.5}{1 - \lambda} + \frac{0.5}{2 - \lambda} + \frac{0.5}{3 - \lambda} + \frac{0.5}{4 - \lambda}</math>]] | ||
| − | + | По рисунку можно заметить, что прямая <math>y = 1</math> является горизонтальной асимптотой для данного графика, а прямые <math>\lambda = d_{i}</math> есть вертикальные асимптоты. Так как <math>f^{'}(\lambda) = \rho \sum_{i=1, n} \frac{u_{i}^{2}} {(d_{i}-\lambda)^{2}}> 0 </math>, функция возрастает всюду, кроме точек <math>\lambda = d_{i}</math>. Из этого следует, что корни функции разделяются числами <math>d_{i}</math> и ещё один корень находится справа от точки <math>d_{1}</math> (на рис. 1 <math>d_{1} = 4</math>). (При <math>\rho<0</math> функция <math>f(\lambda)</math> всюду убывает и соответствующий корень будет находиться слева от точки <math>d_{n}</math>). Для функции <math>f(\lambda)</math>, которая является монотонной и гладкой на каждом из интервалов <math>(d_{i+1},d_{i})</math>, можно найти вариант метода Ньютона, который будет быстро и монотонно сходиться к каждому из корней, при условии, что начальная точка взята в <math>(d_{i+1},d_{i})</math>. Нам достаточно знать тот факт, что на практике метод сходится к каждому собственному значению за строго ограниченное число шагов. Поскольку вычисление <math>f(\lambda)</math> и <math>f^{'}(\lambda)</math> стоит <math>O(n)</math> флопов, для вычисления одного собственного значения достаточно <math>O(n)</math> флопов, следовательно для вычисления всех <math>n</math> собственных значений матрицы <math>D + \rho uu^{T}</math> потребуется <math>O(n^{2})</math> флопов. | |
Для собственных векторов матрицы <math>D + \rho uu^{T}</math> мы легко можем получить явные выражения. | Для собственных векторов матрицы <math>D + \rho uu^{T}</math> мы легко можем получить явные выражения. | ||
| − | + | ''Лемма 2.'' Если <math>\alpha</math> - собственное значение матрицы <math>D + \rho uu^{T}</math>, то соответствующий вектор равен <math>(D - \alpha I)^{-1}u</math>. Поскольку матрица <math>D - \alpha I</math> диагональная, для вычисления такого вектора достаточно <math>O(n)</math> флопов. | |
Доказательство. | Доказательство. | ||
| + | <math>(D + \rho uu^{T})[(D - \alpha I)^{-1}u] = | ||
| + | |||
| + | (D - \alpha I + \alpha I + \rho uu^{T})(D - \alpha I)^{-1}u = | ||
| + | |||
| + | u + \alpha (D - \alpha I)^{-1}u + u[\rho u^{T}(D - \alpha I)^{-1}u]= </math> | ||
| − | + | <math> = u + \alpha(D - \alpha I)^{-1}u - u = \alpha [(D - \alpha I)^{-1}u]</math>, | |
| − | <math> = u + \alpha(D - \alpha I)^{-1}u - u = \alpha [(D - \alpha I)^{-1}u]</math>, | ||
| − | + | поскольку | |
| − | + | <math> \rho u^{T}(D - \alpha I)^{-1}u + 1 = f(\alpha) = 0 </math>. | |
| − | + | Что и требовалось доказать. | |
| − | + | Получается, что для вычисления по этой простой формуле всех <math>n</math> собственных векторов потребуется <math>O(n^{2})</math> флопов. К сожалению, данная формула не обеспечивает нам численной устойчивости, так как для двух очень близких значений <math>\alpha_{i}</math> может давать неортогональные приближенные собственные векторы <math>u_{i}</math>. Учёным потребовалось целое десятилетие для того, чтобы найти устойчивую альтернативу исходному описанию алгоритма. Подробнее детали будут обсуждаться ниже в данном разделе. | |
| − | + | Алгоритм является рекурсивным. | |
| − | + | До сих пор полагалось, что все <math>d_{i}</math> различны и все <math>u_{i}</math> отличны от нуля. Если это будет не так, то вековое уравнение <math>f(\lambda)=0</math> имеет <math>k</math> вертикальных асимптот, где <math>k<n</math>, а следовательно <math>k</math> корней. Однако оказывается, что остальные <math>n - k</math> собственных значений могут быть определены без каких-либо усилий: в случае, если <math>d_{i}=d_{i+1}</math> или <math>u_{i}=0</math>, легко показать, что <math>d_{i}</math> является собственным значением и для матрицы <math>D + \rho uu^{T}</math>. В такой ситуации мы говорим о '''дефляции'''. На практике выбирается некоторое пороговое значение и дефляция для числа <math>d_{i}</math> регистрируется, в том случает, если в смысле этого порога <math>d_{i}</math> достаточно близко к <math>d_{i+1}</math> либо <math>u_{i}</math> достаточно мало. | |
| − | |||
| − | |||
| − | + | Основной выигрыш от использования дефляции состоит не в том, что убыстряется решение векового уравнения - этот этап в любом случае стоит лишь <math>O(n^{2})</math> операций. Выигрыш заключается в ускорении матричного умножения на последнем шаге алгоритма. Действительно, если <math>u_{i}=0</math>, то соответствующий собственный вектор есть i-й столбец <math>e_{i}</math> единичной матрицы. Это означает, что <math>e_{i}</math> является i-м столбцом в матрице <math>Q_{'}</math>, следовательно при формировании матрицы <math>Q</math> применяя левое умножение <math>Q_{1}</math> на <math>Q_{2}</math> вычисление i-го столбца не будет требовать никаких затрат. Аналогичное упрощение возможно в случае <math>d_{i} = d_{i+1}</math>. При дефляции многих собственных значений устраняется большая часть работы, которая связана с матричным умножением. | |
| − | |||
| − | + | Далее пойдет речь о решении '''векового уравнения''', которое является одной из основных частей алгоритма. | |
| − | |||
Предположим, что некоторое <math>u_{i}</math>, хотя и мало, все же недостаточно мало для того, чтобы была зарегистрирована дефляция. В этом случае применение метода Ньютона к решению векового уравнения встречается с затруднениями. Вспомним, что пересчет приближённого решения <math>u_{j}</math> уравнения <math>f(\lambda) = 0</math> в методе Ньютона основан на следующих положениях: | Предположим, что некоторое <math>u_{i}</math>, хотя и мало, все же недостаточно мало для того, чтобы была зарегистрирована дефляция. В этом случае применение метода Ньютона к решению векового уравнения встречается с затруднениями. Вспомним, что пересчет приближённого решения <math>u_{j}</math> уравнения <math>f(\lambda) = 0</math> в методе Ньютона основан на следующих положениях: | ||
| − | + | 1. Вблизи точки <math>\lambda = \lambda_{j}</math> функция <math>f(\lambda)</math> аппроксимируется линейной функцией <math>l(\lambda)</math>; график есть прямая линия, касающаяся графика функции <math>f(\lambda)</math> при <math>\lambda = \lambda_{j}</math>. | |
| − | + | 2. В качестве <math>\lambda_{j+1}</math> берётся нуль этого линейного приближения, т.е. <math>l(\lambda_{j+1})=0</math>. | |
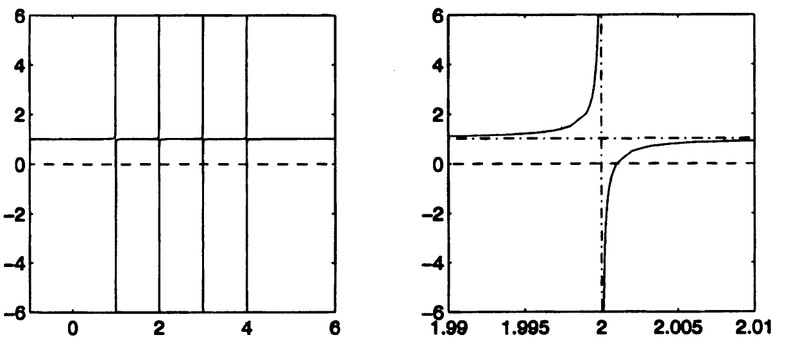
Функция, показанная на рис.1, не доставляет видимых трудностей методу Ньютона, поскольку вблизи каждого своего нуля <math>f(\lambda)</math> достаточно хорошо аппроксимируется линейными функциями. Однако рассмотрим график функции на рис. 2. Она получена из функции на рис. 1 заменой значения .5 для <math>u_{i}^{2}</math> на .001. Это новое значение недостаточно мало для того, чтобы вызвать дефляцию. График функции в левой части рис.2 визуально не отличим от её вертикальных и горизонтальных асимптот, поэтому в правой части укрупненно воспроизведён фрагмент графика, прилегающий к вертикальной асимптоте <math>\lambda = 2</math>. Видно, что график слишком быстро "выполняет поворот" и для большей части значений <math>\lambda</math> почти горизонтален. Поэтому, применяя метод Ньютона почти к любому начальному приближению <math>\lambda_{0}</math>, мы получаем линейное приближение <math>l(\lambda)</math> с почти горизонтальным графиком и малым положительным угловым коэффициентом. В результате <math>\lambda_{1}</math> является отрицательным числом, огромным по абсолютной величине, которое совершенно бесполезно в качестве приближения к истинному корню. | Функция, показанная на рис.1, не доставляет видимых трудностей методу Ньютона, поскольку вблизи каждого своего нуля <math>f(\lambda)</math> достаточно хорошо аппроксимируется линейными функциями. Однако рассмотрим график функции на рис. 2. Она получена из функции на рис. 1 заменой значения .5 для <math>u_{i}^{2}</math> на .001. Это новое значение недостаточно мало для того, чтобы вызвать дефляцию. График функции в левой части рис.2 визуально не отличим от её вертикальных и горизонтальных асимптот, поэтому в правой части укрупненно воспроизведён фрагмент графика, прилегающий к вертикальной асимптоте <math>\lambda = 2</math>. Видно, что график слишком быстро "выполняет поворот" и для большей части значений <math>\lambda</math> почти горизонтален. Поэтому, применяя метод Ньютона почти к любому начальному приближению <math>\lambda_{0}</math>, мы получаем линейное приближение <math>l(\lambda)</math> с почти горизонтальным графиком и малым положительным угловым коэффициентом. В результате <math>\lambda_{1}</math> является отрицательным числом, огромным по абсолютной величине, которое совершенно бесполезно в качестве приближения к истинному корню. | ||
| Строка 127: | Строка 138: | ||
Чтобы найти выход из этого положения, можно модифицировать метод Ньютона следующим образом: раз <math>f(\lambda)</math> нельзя хорошо приблизить линейной функцией <math>l(\lambda)</math>, попробуем взять в качестве приближения какую-нибудь другую простую функцию <math>h(\lambda)</math>. Нет ничего особого именно в прямых линиях: для метода Ньютона вместо <math>l(\lambda)</math> можно взять любое приближение <math>h(\lambda)</math>, значения и нули которого легко вычисляются. Функция <math>f(\lambda)</math> имеет полюсы в точках <math>d_{i}</math> и <math>d_{i+1}</math>, которые определяют её поведение в соответствующих окрестностях. Поэтому при поиске корня в интервале <math>(d_{i+1}, d_{i})</math> естественно выбрать функцию <math>h(\lambda)</math>, также имеющую эти полюсы, т.е. функцию вида | Чтобы найти выход из этого положения, можно модифицировать метод Ньютона следующим образом: раз <math>f(\lambda)</math> нельзя хорошо приблизить линейной функцией <math>l(\lambda)</math>, попробуем взять в качестве приближения какую-нибудь другую простую функцию <math>h(\lambda)</math>. Нет ничего особого именно в прямых линиях: для метода Ньютона вместо <math>l(\lambda)</math> можно взять любое приближение <math>h(\lambda)</math>, значения и нули которого легко вычисляются. Функция <math>f(\lambda)</math> имеет полюсы в точках <math>d_{i}</math> и <math>d_{i+1}</math>, которые определяют её поведение в соответствующих окрестностях. Поэтому при поиске корня в интервале <math>(d_{i+1}, d_{i})</math> естественно выбрать функцию <math>h(\lambda)</math>, также имеющую эти полюсы, т.е. функцию вида | ||
| − | + | <math>h(\lambda)= \frac{c_{1}}{d_{i}-\lambda} + \frac{c_{2}}{d_{i+1}-\lambda} + c_{3}</math> | |
Константы <math>c_{1},c_{2}</math> и <math>c_{3}</math> обеспечивающие, что <math>h(\lambda)</math> есть приближение к <math>f(\lambda)</math>, можно выбрать несколькими способами. Отметим, что если <math>c_{1},c_{2}</math> и <math>c_{3}</math> уже известны, то уравнение <math>h(\lambda)=0</math> легко решается относительно <math>\lambda</math>, поскольку сводится к эквивалентному квадратному уравнению | Константы <math>c_{1},c_{2}</math> и <math>c_{3}</math> обеспечивающие, что <math>h(\lambda)</math> есть приближение к <math>f(\lambda)</math>, можно выбрать несколькими способами. Отметим, что если <math>c_{1},c_{2}</math> и <math>c_{3}</math> уже известны, то уравнение <math>h(\lambda)=0</math> легко решается относительно <math>\lambda</math>, поскольку сводится к эквивалентному квадратному уравнению | ||
| − | + | <math>c_{1}(d_{i+1}-\lambda)+c_{2}(d_{i}-\lambda)+c_{3}(d_{i}-\lambda)(d_{i+1}-\lambda)=0</math> | |
Пусть <math>\lambda_{j}</math> - приближённое значение корня. определим <math>c_{1},c_{2}</math> и <math>c_{3}</math> так, чтобы | Пусть <math>\lambda_{j}</math> - приближённое значение корня. определим <math>c_{1},c_{2}</math> и <math>c_{3}</math> так, чтобы | ||
| − | + | <math>\frac{c_{1}}{d_{i}-\lambda} + \frac{c_{2}}{d_{i+1}-\lambda} + c_{3} = h(\lambda) \approx f(\lambda) = 1 + \rho \sum_{k=1, n} \frac{u_{k}^{2}} {d_{k}-\lambda} </math> | |
| − | |||
для <math>\lambda</math> в окрестности <math>\lambda_{j}</math>. Заметим, что | для <math>\lambda</math> в окрестности <math>\lambda_{j}</math>. Заметим, что | ||
| − | + | <math>f(\lambda) = 1 + \rho \sum_{k=1, i} \frac{u_{k}^{2}} {d_{k}-\lambda} + \rho \sum_{k=i+1, n} \frac{u_{k}^{2}} {d_{k}-\lambda} \equiv 1 + \psi_{1}(\lambda) + \psi_{2}(\lambda)</math>. | |
| − | |||
Если <math>\lambda \in (d_{i+1},d_{i})</math>, то <math>\psi_{1}(\lambda)</math> есть сумма положительных слагаемых, а <math>\psi_{2}(\lambda)</math> - сумма отрицательных. Поэтому и <math>\psi_{1}(\lambda)</math>, и <math>\psi_{2}(\lambda)</math> могут быть вычислены с высокой точностью; однако при их сложении вполне вероятно взаимное уничтожение верных разрядов и потеря относительной точности в сумме. Возьмем числа <math>c_{1}</math> и <math>\hat{c_{1}}</math>, такие, что функция | Если <math>\lambda \in (d_{i+1},d_{i})</math>, то <math>\psi_{1}(\lambda)</math> есть сумма положительных слагаемых, а <math>\psi_{2}(\lambda)</math> - сумма отрицательных. Поэтому и <math>\psi_{1}(\lambda)</math>, и <math>\psi_{2}(\lambda)</math> могут быть вычислены с высокой точностью; однако при их сложении вполне вероятно взаимное уничтожение верных разрядов и потеря относительной точности в сумме. Возьмем числа <math>c_{1}</math> и <math>\hat{c_{1}}</math>, такие, что функция | ||
| + | <math>h_{1}(\lambda) \equiv \hat{c_{1}} + \frac{c_{1}}{d_{i}-\lambda}</math> удовлетворяет условиям <math>h_{1}(\lambda_{j}) = \psi_{1}(\lambda_{j})</math> и <math>h_{1}^{'}(\lambda_{j})=\psi_{1}^{'}(\lambda_{j})</math> (*) | ||
| − | + | Это означает, что гипербола, являющаяся графиком функции <math>h_{1}(\lambda)</math>, касается графика функции <math>\psi_{i}(\lambda)</math> при <math>\lambda = \lambda_{j}</math>. Два условия в (*) - это обычные условия метода Ньютона, за исключением того, что вместо прямой в качестве приближения используется гипербола. Легко проверить, что <math>c_{1}=\psi_{1}^{'}(\lambda_{j})(d_{i} - \lambda_{j})^{2}</math> и <math>\hat{c_{1}}=\psi_{1}(\lambda_{j}) - \psi_{1}^{'}(\lambda_{j})(d_{i} - \lambda_{j})</math>. | |
| − | |||
| − | Это означает, что гипербола, являющаяся графиком функции <math>h_{1}(\lambda)</math>, касается графика функции <math>\psi_{i}(\lambda)</math> при <math>\lambda = \lambda_{j}</math>. Два условия в ( | ||
Подобным же образом выбираем <math>c_{2}</math> и <math>\hat{c_{2}}</math> так, чтобы функция | Подобным же образом выбираем <math>c_{2}</math> и <math>\hat{c_{2}}</math> так, чтобы функция | ||
| + | <math>h_{2}(\lambda) \equiv \hat{c_{2}} + \frac{c_{2}}{d_{i+1}-\lambda}</math> удовлетворяла условиям | ||
| + | <math>h_{2}(\lambda_{j}) = \psi_{2}(\lambda_{j})</math> и <math>h_{2}^{'}(\lambda_{j})=\psi_{2}^{'}(\lambda_{j})</math> | ||
| − | + | Наконец, полагаем | |
| + | <math>h(\lambda) = 1 + h_{1}(\lambda) + h_{2}(\lambda) = (1 + \hat{c_{1}} + \hat{c_{2}} + \frac{c_{1}}{d_{i}-\lambda} + \frac{c_{2}}{d_{i+1}-\lambda} \equiv c_{3} + \frac{c_{1}}{d_{i}-\lambda} + \frac{c_{2}}{d_{i+1}-\lambda}</math>. | ||
| − | + | == Вычислительное ядро алгоритма == | |
| + | Вычислительным ядром последовательной схемы решения будет являться вычисление матрицы <math>Q</math> собственных векторов при помощи умножения матрицы <math>Q = \begin{bmatrix} Q_{1} & 0 \\ 0 & Q_{2}\end{bmatrix} </math> на матрицу <math>Q^{'}</math>. Эта операция имеет сложность <math>cn^{3}</math> о чём будет говориться ниже, в разделе [[#Последовательная сложность алгоритма]] . | ||
| − | + | Данной операции предшествует вычисление собственных значений и векторов матрицы <math> D + \rho uu^{T}</math>. | |
| − | + | == Макроструктура алгоритма == | |
| − | + | В разделе [[#Информационный граф]] описана структура алгоритма, в которой есть блок умножения матриц для вычисления собственных векторов, являющийся вычислительным ядром алгоритма. В соответствующем разделе ([[#Вычислительное ядро алгоритма]]) мы упоминали о том, что данному блоку предшествует вычисление собственных значений, которое производится [https://ru.wikipedia.org/wiki/%D0%9C%D0%B5%D1%82%D0%BE%D0%B4_%D0%9D%D1%8C%D1%8E%D1%82%D0%BE%D0%BD%D0%B0 методом Ньютона]. | |
| − | |||
| − | |||
| − | |||
== Схема реализации последовательного алгоритма == | == Схема реализации последовательного алгоритма == | ||
| − | + | Рассмотрим каким именно образом происходит вычисление собственных значений и собственных векторов симметричной трехдиагональной матрицы при помощи стратегии "разделяй и властвуй": | |
| − | |||
''proc dc_eig''<math>(T,Q,\Lambda)...</math> по входной матрице <math>T</math> вычисляются выходные матрицы <math>Q</math> и <math>\Lambda</math>, такие, что <math>T = Q\Lambda Q^{T}</math> | ''proc dc_eig''<math>(T,Q,\Lambda)...</math> по входной матрице <math>T</math> вычисляются выходные матрицы <math>Q</math> и <math>\Lambda</math>, такие, что <math>T = Q\Lambda Q^{T}</math> | ||
| − | ''' | + | В случае, '''если''' <math>T</math> - матрица размера <math>1</math> x <math>1</math> : |
| − | + | 1. Присвоить выходным параметрам значения <math> Q = 1, \Lambda = T</math> | |
| − | '''Иначе''' | + | '''Иначе''': |
| − | + b_{m}vv^{T} </math> | + | 1. Представить <math>T</math> в виде <math> T = \begin{bmatrix} T_{1} & 0 \\ 0 & T_{2}\end{bmatrix} + b_{m}vv^{T} </math> |
| − | + | 2. ''call dc_eig''<math>(T_{1},Q_{1},\Lambda_{1})</math> | |
| − | + | 3. ''call dc_eig''<math>(T_{2},Q_{2},\Lambda_{2})</math> | |
| − | + | 4. Построить <math>D+\rho uu^{T}</math> по <math> \Lambda_{1},\Lambda_{2}, Q_{1}, Q_{2}</math> | |
| − | + | 5. Найти матрицу собственных значений <math>\Lambda</math> | |
| − | + | 6. Найти матрицу собственных векторов <math>Q^{'}</math> для матрицы <math>D+\rho uu^{T}</math> | |
| − | * Q^{'} </math> | + | 7. Построить матрицу собственных векторов <math>Q</math> для матрицы <math>T</math> : <math> Q = \begin{bmatrix} Q_{1} & 0 \\ 0 & Q_{2}\end{bmatrix} * Q^{'} </math> |
| − | + | 8. Присвоить выходным параметрам значения <math>Q</math> и <math>\Lambda</math> | |
'''endif''' | '''endif''' | ||
== Последовательная сложность алгоритма == | == Последовательная сложность алгоритма == | ||
| − | + | Рассмотрим сложность алгоритма. Пусть <math>t(n)</math> - число флопов, которое потребуется при обработке матрицы размера <math> n * | |
| + | n</math> процедурой ''dc_eig''. В таком случае | ||
| + | |||
| + | <math> t(n) = 2t(n/2) </math> два рекурсивных обращения к ''dc_eig''<math>(T_{i},Q_{i},\Lambda_{i})</math> | ||
| + | <math> +O(n^{2})</math> вычисление собственных значений матрицы <math>D+\rho uu^{T}</math> | ||
| + | <math> +O(n^{2})</math> вычисление собственных векторов матрицы <math>D+\rho uu^{T}</math> | ||
| + | <math> +c*n^{3}</math> вычисление матрицы <math>Q = \begin{bmatrix} Q_{1} & 0 \\ 0 & Q_{2}\end{bmatrix} *Q^{'}</math> | ||
| + | |||
| + | |||
| + | Если <math> Q_{1}, Q_{2}</math> и <math>Q^{'}</math> рассматривать как плотные матрицы и использовать стандартный алгоритм матричного умножения, то константа <math> c </math> в последней строке будет равна 1. Следовательно, именно это умножение и будет составлять наиболее трудоёмкую часть алгоритма в целом. Игнорируя члены порядка <math>n^{2}</math>, получаем <math>t(n) = 2t(n/2) + cn^{3}</math>. Решив это разностное уравнение, находим <math> t \approx c\frac{4}{3}n^{3} </math> | ||
| + | |||
| + | На практике константа <math>c</math> обычно оказывается гораздо меньше 1, так как матрица <math>Q^{'}</math> весьма разрежена вследствие явления, которое называется дефляцией, и которое было описано выше. | ||
| − | + | == Информационный граф == | |
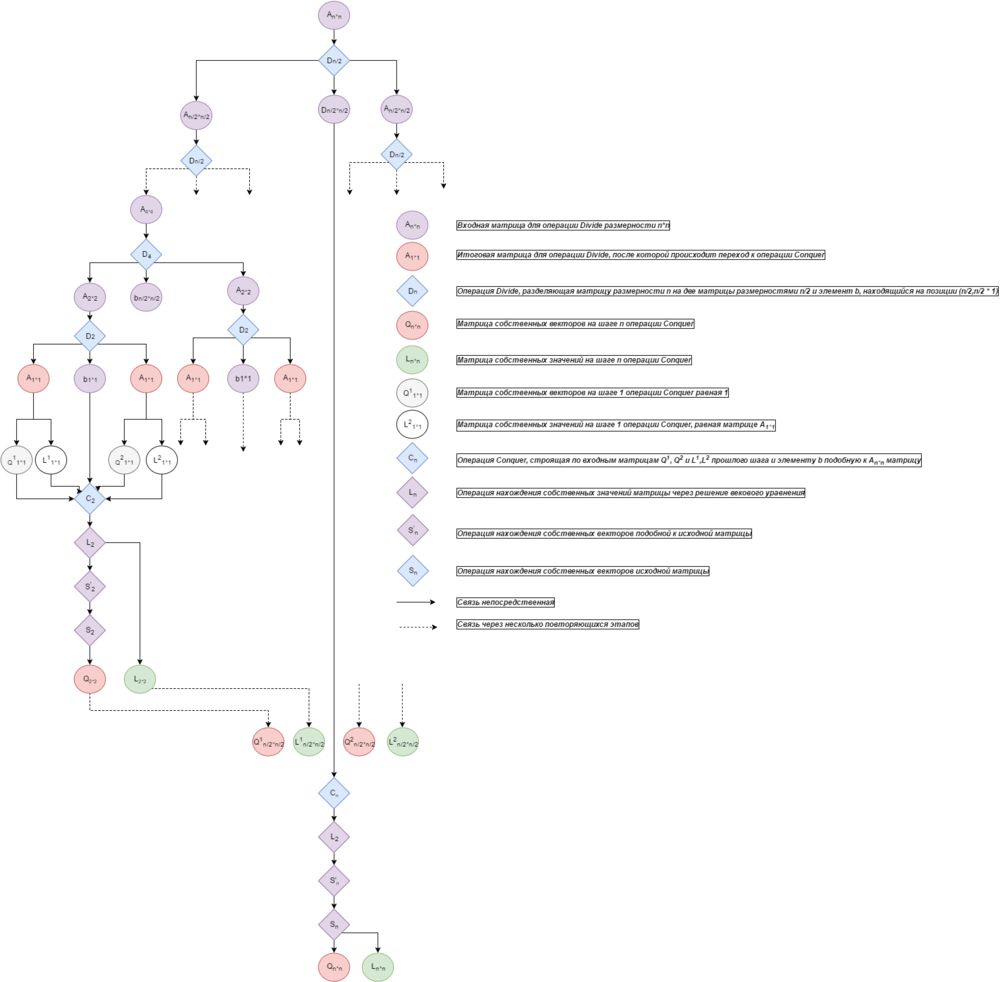
| + | На рисунке 3 изображена структура алгоритма. | ||
| − | + | [[File:Sergeev_5.png|thumb|center|left|1000px|Рис. 3. Дерево алгоритма "Разделяй и властвуй"]] | |
| − | |||
| − | *Q^{'}</math> | + | Операции: |
| + | <math>D</math> - операция Divide разделения матрицы <math> T </math> на матрицы <math>T_{1}</math> и <math>T_{2}</math> | ||
| − | + | Индексы - размерность | |
| − | + | <math>S_{k}</math> - операция Conquer сбора матрицы <math> D </math> | |
| − | + | <math> L_{k} </math> - операция поиска собственных значений | |
| − | + | ||
| − | + | <math> S^{'} </math> - операция поиска собственных векторов матрицы <math> Q^{'} </math> | |
| − | + | <math> S </math> - операция поиска собственных векторов матрицы <math> Q </math> | |
== Ресурс параллелизма алгоритма == | == Ресурс параллелизма алгоритма == | ||
| − | + | В структуре алгоритма имеем два параллельных блока - вызов рекурсивных функций ''dc_eig'' для вычисления собственных значений и векторов матриц <math>T_{1}</math> и <math>T_{2}</math> - это единственная часть алгоритма, в которой возможно использовать параллелизм. | |
| + | |||
| + | Рекурсивное разделение матрицы ведёт к иерархии вычислительных подблоков с графом зависимости данных, который принимает вид двоичного дерева. Такая структура является естественным путем разделения вычислений между процессорами. | ||
| + | |||
| + | - В вершине дерева все процессы взаимодействуют. | ||
| + | |||
| + | - В каждой ветви дерева вычисление делится на два вычислительных подблока, внутри каждого из которых процессы параллельно взаимодействуют. | ||
| + | |||
| + | - В листьях деревьев каждый процесс занимается вычислением независимо. | ||
| + | |||
| + | В случае реализации без параллелизма, функции ''dc_eig'' отрабатывают последовательно - сначала со входными параметрами <math>T_{1}, Q_{1}, \Lambda_{1}</math>, затем - <math>T_{2}, Q_{2}, \Lambda_{2}</math>. | ||
| + | |||
| + | Таким образом, благодаря параллелизму высота алгоритма параллельного составляет <math>log_{2}(n)</math>, тогда как при последовательной реализации высота алгоритма равна сумме геометрической прогрессии <math>1+2+4+8+...+2^{n-1} = 2^{n} - 1</math>, что значительно сокращает число итераций алгоритма. | ||
| + | |||
| + | Поскольку функции являются рекурсивными, их параллельный вызов даст значительный выигрыш во времени. | ||
| + | |||
| + | При размерности матрицы больше 3 параллельная реализация позволяет сократить количество этапов работы алгоритма больше, чем в два раза. | ||
== Входные и выходные данные алгоритма == | == Входные и выходные данные алгоритма == | ||
| − | + | '''Входные данные''': трёхдиагональная симметрическая матрица, описанная в разделе [[#Математическое описание алгоритма]]. | |
| + | |||
| + | <math> | ||
| + | L = \begin{bmatrix} | ||
| + | a_{1} & b_{1}&&&&& \\ | ||
| + | b_{1} & \ddots & \ddots \\ | ||
| + | & \ddots & a_{m-1} & b_{m-1} \\ | ||
| + | && b_{m-1} & a_{m} & b_{m} \\ | ||
| + | &&& b_{m} & a_{m+1} & b_{m+1} \\ | ||
| + | &&&& b_{m+1} & \ddots \\ | ||
| + | &&&&&& \ddots & b_{n-1} \\ | ||
| + | &&&&&& b_{n-1} & a_{n} \\ | ||
| + | \end{bmatrix} | ||
| + | </math> | ||
| + | |||
| + | '''Объём входных данных''': <math> 2n + 1 </math> (в силу симметричности достаточно хранить только диагональ и над/под диагональные элементы). | ||
| + | |||
| + | '''Выходные данные''': Вектор собственных значений длины <math> n </math> и <math> n </math> собственных векторов длины <math> n </math> , соответствующих собственным значениям исходной матрицы. | ||
| − | + | '''Объём выходных данных''': <math>n(n + 1) </math> | |
== Свойства алгоритма == | == Свойства алгоритма == | ||
| − | + | Данный алгоритм является самым быстрым алгоритмом среди существующих: Разделяй и властвуй, QR, Бисекция и обратная итерация. | |
| + | |||
| + | '''Последовательная сложность данного алгоритма:''' <math> t = c\frac{4}{3}n^{3} </math> | ||
| − | + | Она удовлетворяет соотношению <math>t(n) = n^3 +2t(\frac{n}{2})</math> | |
| − | Параллельная сложность алгоритма ( | + | '''Параллельная сложность алгоритма (за счет дефляции):''' <math> O(n^{2.3})</math>; в крайне редких случаях: <math> O(n^{2}) </math>. |
| − | Особенности алгоритма: | + | '''Особенности алгоритма:''' |
| − | 1. | + | 1. Дефляция ([[#Дефляция]]) |
| − | 2. | + | 2. Адаптированный метод Ньютона ([[#Макроструктура алгоритма]]) |
| − | = | + | = Программная реализация алгоритма = |
Вторая часть описания алгоритмов в рамках AlgoWiki рассматривает все составные части процесса их реализации. Рассматривается как последовательная реализация алгоритма, так и параллельная. Описывается взаимосвязь свойств программ, реализующих алгоритм, и особенностей архитектуры компьютера, на которой они выполняются. Исследуется работа с памятью, локальность данных и вычислений, описывается масштабируемость и эффективность параллельных программ, производительность компьютеров, достигаемая на данной программе. Обсуждаются особенности реализации для разных классов архитектур компьютеров, приводятся ссылки на реализации в существующих библиотеках. | Вторая часть описания алгоритмов в рамках AlgoWiki рассматривает все составные части процесса их реализации. Рассматривается как последовательная реализация алгоритма, так и параллельная. Описывается взаимосвязь свойств программ, реализующих алгоритм, и особенностей архитектуры компьютера, на которой они выполняются. Исследуется работа с памятью, локальность данных и вычислений, описывается масштабируемость и эффективность параллельных программ, производительность компьютеров, достигаемая на данной программе. Обсуждаются особенности реализации для разных классов архитектур компьютеров, приводятся ссылки на реализации в существующих библиотеках. | ||
| Строка 242: | Строка 297: | ||
== Возможные способы и особенности параллельной реализации алгоритма == | == Возможные способы и особенности параллельной реализации алгоритма == | ||
== Масштабируемость алгоритма и его реализации == | == Масштабируемость алгоритма и его реализации == | ||
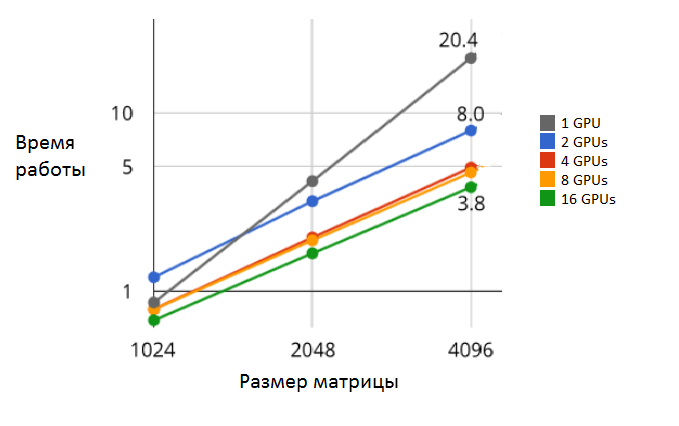
| − | + | Тестирование реализации алгоритма проводилось на суперкомпьютере "Ломоносов" с использованием 1, 2, 4, 8, 16 процессоров на матрицах размера от 4 до 4096. Реализация произведена на библиотеке OpenMP. | |
| + | |||
| + | Общая эффективность программы увеличивается при увеличении числа процессоров (за счет сокращения времени работы программы) и уменьшается при увеличении размера матрицы (за счет увеличения времени обработки входных данных). При одновременном увеличении числа процессоров и размерности матрицы общая эффективность падает. | ||
| + | |||
| + | Ниже приведена схема зависимости времени работы программы от размера матрицы при разном числе процессоров. При размере матрицы от 4 до 1024 время работы очень мало, поэтому эти данные не указаны на схеме. | ||
| + | |||
| + | [[File:DivAndConq11.png|thumb|center|left|1000px|Рис. 4. Зависимость времени работы от размера матрицы]] | ||
| + | |||
| + | Параметры компиляции и запуска: | ||
| + | |||
| + | ssh compiler | ||
| + | module add slurm | ||
| + | module add openmpi/1.5.5-icc | ||
| + | g++ _scratch/DivideAndConquer.c++ -fopenmp -std=c++0x -o DC | ||
| + | sbatch -p test -n1 run ./DC | ||
| + | |||
| + | Код реализации: https://drive.google.com/open?id=0B0G2UV7cuLwHQk9xd1lyeDNJOXc | ||
== Динамические характеристики и эффективность реализации алгоритма == | == Динамические характеристики и эффективность реализации алгоритма == | ||
| Строка 249: | Строка 320: | ||
== Существующие реализации алгоритма == | == Существующие реализации алгоритма == | ||
| − | + | Единственный найденный пример реализации описан в [http://www.netlib.org/lapack/lawnspdf/lawn132.pdf Francoise Tisseury, Jack Dongarra, "Parallelizing the Divide and Conquer Algorithm for the Symmetric Tridiagonal Eigenvalue Problem on Distributed Memory Architectures" ] ([3] с. 7, 19-20). | |
= Литература = | = Литература = | ||
| + | |||
[1] Дж. Деммель, «Вычислительная линейная алгебра» //С. 230-235 | [1] Дж. Деммель, «Вычислительная линейная алгебра» //С. 230-235 | ||
| − | [2] [http://www. | + | [2] [http://www.cscamm.umd.edu/tadmor/pub/linear-stability/Gill_Tadmor_SISC90.pdf Doron Grill and Eitan Tadmor AN <math>O(N2)</math> METHOD FOR COMPUTING THE EIGENSYSTEM OF <math>N</math>x<math>N</math> SYMMETRIC TRIDIAGONAL MATRICES BY THE DIVIDE AND CONQUER APPROACH] |
| − | [3] [http://www.netlib.org/ | + | [3] [http://www.netlib.org/utk/people/JackDongarra/PAPERS/104_1999_a-parallel-divide-and-conquer-algorithm.pdf Francoise Tisseury, Jack Dongarra, A Parallel Divide and Conquer Algorithm for the Symmetric Eigenvalue Problem on Distributed Memory Architectures] |
| − | [4] [ | + | [4] [http://www.netlib.org/lapack/lawnspdf/lawn132.pdf Francoise Tisseury, Jack Dongarra, Parallelizing the Divide and Conquer Algorithm for the Symmetric Tridiagonal Eigenvalue Problem on Distributed Memory Architectures] |
| − | [5] [ | + | [5] [https://en.wikipedia.org/wiki/Divide-and-conquer_eigenvalue_algorithm Алгоритм "Разделяй и властвуй" - Wikipedia] |
[[en:Description of algorithm properties and structure]] | [[en:Description of algorithm properties and structure]] | ||
Текущая версия на 13:28, 9 января 2017
 | Эта работа прошла предварительную проверку Дата последней правки страницы: 09.01.2017 Данная работа соответствует формальным критериям. Проверено IgorS. |
Авторы статьи: Сергеев Никита (группа 614) (1.1, 1.2, 1.5, 1.6, 1.7, 1.8, 1.10, 2.4), Стрельцова Виктория (группа 614) (1.2, 1.3, 1.4, 1.6, 1.7, 1.9, 1.10, 2.4)
| Метод "Разделяй и властвуй" вычисления собственных значений и векторов трёхдиагональной матрицы | |
| Последовательный алгоритм | |
| Последовательная сложность | c\frac{4}{3}n^{3} |
| Объём входных данных | 2n + 1 |
| Объём выходных данных | n(n + 1) |
| Параллельный алгоритм | |
| Параллельная сложность | O(n^{2.3})
крайне редко: O(n^{2}) |
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Метод разделяй и властвуй вычисления собственных значений и векторов трёхдиагональной матрицы - является наиболее быстрым из существующих методов вычисления всех собственных значений и собственных векторов трехдиагональной матрицы, начиная с порядка n, который примерно равен 26. (Точное значение этого порогового порядка в конкретном случае зависит от компьютера.)
Численно устойчивая реализация данного метода весьма не тривиальна, так как не смотря на то, что впервые метод был предложен в 1981 г., "правильный" способ реализации метода был найден лишь в 1992 г. Этот способ был воплощен при помощи LAPACK-программ ssyevd (для плотных матриц) и sstevd (для трехдиагональных матриц). В этих программах стратегия "разделяй-и-влавствуй" используется для матриц порядка выше 25.
Для матриц порядка ниже 25 (или в тех случаях, когда требуются только собственные значения) автоматически происходит переход к методу QR-итерации.
1.2 Математическое описание алгоритма
Пусть
- L = \begin{bmatrix} a_{1} & b_{1}&&&&& \\ b_{1} & \ddots & \ddots \\ & \ddots & a_{m-1} & b_{m-1} \\ && b_{m-1} & a_{m} & b_{m} \\ &&& b_{m} & a_{m+1} & b_{m+1} \\ &&&& b_{m+1} & \ddots \\ &&&&&& \ddots & b_{n-1} \\ &&&&&& b_{n-1} & a_{n} \\ \end{bmatrix} = \begin{bmatrix} a_{1} & b_{1} &&&&& \\ b_{1} & \ddots & \ddots \\ & \ddots & a_{m-1} & b_{m-1} \\ && b_{m-1} & a_{m} - b_{m} \\ &&&& a_{m+1} - b_{m} & b_{m+1} \\ &&&& b_{m+1} & \ddots \\ &&&&&& \ddots & b_{n-1} \\ &&&&&& b_{n-1} & a_{n} \\ \end{bmatrix} +
+ \begin{bmatrix} &&&&&&& \\ &&&&&&& \\ &&&b_{m} & b_{m} \\ &&&b_{m} & b_{m} \\ &&&&&&& \\ &&&&&&& \\ \end{bmatrix} = \begin{bmatrix} T_{1} & 0 \\ 0 & T_{2}\end{bmatrix} + b_{m} * \begin{bmatrix} 0 \\ \vdots \\ 0 \\ 1 \\ 1 \\ 0 \\ \vdots \\ 0 \end{bmatrix} \begin{bmatrix} 0 , \ldots , 0 , 1 , 1 , 0 \ldots , 0 \end{bmatrix} \equiv \begin{bmatrix} T_{1} & 0 \\ 0 & T_{2}\end{bmatrix} + b_{m}vv^{T}
В предположении, что известны спектральные разложения матриц T_{1} и T_{2}: T_{i}=Q_{i} \Lambda_{i} Q_{i}^{T} . На самом деле, они будут вычисляться рекурсивно тем же самым алгоритмом.
Можно установить связь между собственными значениями матрицы Т и собственными значениями матриц T_{1} и T_{2}. Получается:
T = \begin{bmatrix} T_{1} & 0 \\ 0 & T_{2}\end{bmatrix} + b_{m}vv^{T} = \begin{bmatrix} Q_{1} \Lambda_{1} Q_{1}^{T} & 0 \\ 0 & Q_{2} L_{2} Q_{2}^{T}\end{bmatrix} + b_{m}vv^{T} = \begin{bmatrix} Q_{1} & 0 \\ 0 & Q_{2}\end{bmatrix}(\begin{bmatrix} \Lambda_{1} & \\ & \Lambda_{2}\end{bmatrix} + b_{m}vv^{T})\begin{bmatrix} Q_{1}^{T} & 0 \\ 0 & Q_{2}^{T}\end{bmatrix} ,
где u = \begin{bmatrix} Q_{1}^{T} & 0 \\ 0 & Q_{2}^{T}\end{bmatrix}v - матрица, в первой строке которой находятся элементы последнего столбца матрицы Q_{1}^{T}, а во второй - элементы первого столбца матрицы Q_{2}^{T}, так как v = \begin{bmatrix} 0 , \ldots , 0 , 1 , 1 , 0 \ldots , 0 \end{bmatrix}^T. Следовательно, T имеет такие же собственные значения, что и подобная ей матрица D + \rho uu^{T}, где D = \begin{bmatrix} L_{1} & 0 \\ 0 & L_{2}\end{bmatrix} - диагональная матрица, \rho = b_{m} - число, а u - вектор. В дальнейшем предполагаем, не ограничивая общности, что диагональные элементы d_{1}, \ldots, d_{n} матрицы D упорядочены по не возрастанию: d_{n} \lt = \ldots \lt =d_{1}.
Для того, чтобы найти собственные значения матрицы D + \rho uu^{T}, потребуется вычислить её характеристический многочлен, считая пока матрицу D - \lambda I невырожденной. Тогда получаем det(D + \rho uu^{T} - \lambda I) = det((D - \lambda I)(I + \rho (D- \lambda I)^{-1} uu^{T})).
Так как D - \lambda I невырожденная, det(I + \rho (D - \lambda I)^{-1}uu^{T}) = 0 тогда и только тогда, когда \lambda - является собственным значением. Можем заметить, что матрица I + \rho (D - \lambda I)^{-1}uu^{T} получается из единичной путём добавления матрицы ранга 1. Определитель такой матрицы не сложно вычислить.
Лемма 1. Справедливо равенство [math]det(I + xy^{T}) = 1 + y^{T}x[/math], где [math]x[/math] и [math]y[/math] - векторы.
Следовательно, получаем det(I + \rho (D - \lambda I)^{-1}uu^{T}) = 1 + \rho u^{T}(D - \lambda I)^{-1}u = 1 + \rho \sum_{i=1, n} \frac{u_{i}^{2}} {d_{i}-\lambda} \equiv f(\lambda) ,
т.е. собственные значения матрицы T являются корнями так называемого векового уравнения f(\lambda) = 0. Если все числа d_{i} различны между собой и все u_{i} \lt \gt 0 (случай общего положения), то f(\lambda) имеет график типа, который показан на рис.1(где n = 4 и \rho \gt 0).
По рисунку можно заметить, что прямая y = 1 является горизонтальной асимптотой для данного графика, а прямые \lambda = d_{i} есть вертикальные асимптоты. Так как f^{'}(\lambda) = \rho \sum_{i=1, n} \frac{u_{i}^{2}} {(d_{i}-\lambda)^{2}}\gt 0 , функция возрастает всюду, кроме точек \lambda = d_{i}. Из этого следует, что корни функции разделяются числами d_{i} и ещё один корень находится справа от точки d_{1} (на рис. 1 d_{1} = 4). (При \rho\lt 0 функция f(\lambda) всюду убывает и соответствующий корень будет находиться слева от точки d_{n}). Для функции f(\lambda), которая является монотонной и гладкой на каждом из интервалов (d_{i+1},d_{i}), можно найти вариант метода Ньютона, который будет быстро и монотонно сходиться к каждому из корней, при условии, что начальная точка взята в (d_{i+1},d_{i}). Нам достаточно знать тот факт, что на практике метод сходится к каждому собственному значению за строго ограниченное число шагов. Поскольку вычисление f(\lambda) и f^{'}(\lambda) стоит O(n) флопов, для вычисления одного собственного значения достаточно O(n) флопов, следовательно для вычисления всех n собственных значений матрицы D + \rho uu^{T} потребуется O(n^{2}) флопов. Для собственных векторов матрицы D + \rho uu^{T} мы легко можем получить явные выражения.
Лемма 2. Если [math]\alpha[/math] - собственное значение матрицы [math]D + \rho uu^{T}[/math], то соответствующий вектор равен [math](D - \alpha I)^{-1}u[/math]. Поскольку матрица [math]D - \alpha I[/math] диагональная, для вычисления такого вектора достаточно [math]O(n)[/math] флопов.
Доказательство. (D + \rho uu^{T})[(D - \alpha I)^{-1}u] = (D - \alpha I + \alpha I + \rho uu^{T})(D - \alpha I)^{-1}u = u + \alpha (D - \alpha I)^{-1}u + u[\rho u^{T}(D - \alpha I)^{-1}u]=
= u + \alpha(D - \alpha I)^{-1}u - u = \alpha [(D - \alpha I)^{-1}u],
поскольку
\rho u^{T}(D - \alpha I)^{-1}u + 1 = f(\alpha) = 0 .
Что и требовалось доказать.
Получается, что для вычисления по этой простой формуле всех n собственных векторов потребуется O(n^{2}) флопов. К сожалению, данная формула не обеспечивает нам численной устойчивости, так как для двух очень близких значений \alpha_{i} может давать неортогональные приближенные собственные векторы u_{i}. Учёным потребовалось целое десятилетие для того, чтобы найти устойчивую альтернативу исходному описанию алгоритма. Подробнее детали будут обсуждаться ниже в данном разделе.
Алгоритм является рекурсивным.
До сих пор полагалось, что все d_{i} различны и все u_{i} отличны от нуля. Если это будет не так, то вековое уравнение f(\lambda)=0 имеет k вертикальных асимптот, где k\lt n, а следовательно k корней. Однако оказывается, что остальные n - k собственных значений могут быть определены без каких-либо усилий: в случае, если d_{i}=d_{i+1} или u_{i}=0, легко показать, что d_{i} является собственным значением и для матрицы D + \rho uu^{T}. В такой ситуации мы говорим о дефляции. На практике выбирается некоторое пороговое значение и дефляция для числа d_{i} регистрируется, в том случает, если в смысле этого порога d_{i} достаточно близко к d_{i+1} либо u_{i} достаточно мало.
Основной выигрыш от использования дефляции состоит не в том, что убыстряется решение векового уравнения - этот этап в любом случае стоит лишь O(n^{2}) операций. Выигрыш заключается в ускорении матричного умножения на последнем шаге алгоритма. Действительно, если u_{i}=0, то соответствующий собственный вектор есть i-й столбец e_{i} единичной матрицы. Это означает, что e_{i} является i-м столбцом в матрице Q_{'}, следовательно при формировании матрицы Q применяя левое умножение Q_{1} на Q_{2} вычисление i-го столбца не будет требовать никаких затрат. Аналогичное упрощение возможно в случае d_{i} = d_{i+1}. При дефляции многих собственных значений устраняется большая часть работы, которая связана с матричным умножением.
Далее пойдет речь о решении векового уравнения, которое является одной из основных частей алгоритма.
Предположим, что некоторое u_{i}, хотя и мало, все же недостаточно мало для того, чтобы была зарегистрирована дефляция. В этом случае применение метода Ньютона к решению векового уравнения встречается с затруднениями. Вспомним, что пересчет приближённого решения u_{j} уравнения f(\lambda) = 0 в методе Ньютона основан на следующих положениях:
1. Вблизи точки \lambda = \lambda_{j} функция f(\lambda) аппроксимируется линейной функцией l(\lambda); график есть прямая линия, касающаяся графика функции f(\lambda) при \lambda = \lambda_{j}.
2. В качестве \lambda_{j+1} берётся нуль этого линейного приближения, т.е. l(\lambda_{j+1})=0.
Функция, показанная на рис.1, не доставляет видимых трудностей методу Ньютона, поскольку вблизи каждого своего нуля f(\lambda) достаточно хорошо аппроксимируется линейными функциями. Однако рассмотрим график функции на рис. 2. Она получена из функции на рис. 1 заменой значения .5 для u_{i}^{2} на .001. Это новое значение недостаточно мало для того, чтобы вызвать дефляцию. График функции в левой части рис.2 визуально не отличим от её вертикальных и горизонтальных асимптот, поэтому в правой части укрупненно воспроизведён фрагмент графика, прилегающий к вертикальной асимптоте \lambda = 2. Видно, что график слишком быстро "выполняет поворот" и для большей части значений \lambda почти горизонтален. Поэтому, применяя метод Ньютона почти к любому начальному приближению \lambda_{0}, мы получаем линейное приближение l(\lambda) с почти горизонтальным графиком и малым положительным угловым коэффициентом. В результате \lambda_{1} является отрицательным числом, огромным по абсолютной величине, которое совершенно бесполезно в качестве приближения к истинному корню.
Чтобы найти выход из этого положения, можно модифицировать метод Ньютона следующим образом: раз f(\lambda) нельзя хорошо приблизить линейной функцией l(\lambda), попробуем взять в качестве приближения какую-нибудь другую простую функцию h(\lambda). Нет ничего особого именно в прямых линиях: для метода Ньютона вместо l(\lambda) можно взять любое приближение h(\lambda), значения и нули которого легко вычисляются. Функция f(\lambda) имеет полюсы в точках d_{i} и d_{i+1}, которые определяют её поведение в соответствующих окрестностях. Поэтому при поиске корня в интервале (d_{i+1}, d_{i}) естественно выбрать функцию h(\lambda), также имеющую эти полюсы, т.е. функцию вида h(\lambda)= \frac{c_{1}}{d_{i}-\lambda} + \frac{c_{2}}{d_{i+1}-\lambda} + c_{3}
Константы c_{1},c_{2} и c_{3} обеспечивающие, что h(\lambda) есть приближение к f(\lambda), можно выбрать несколькими способами. Отметим, что если c_{1},c_{2} и c_{3} уже известны, то уравнение h(\lambda)=0 легко решается относительно \lambda, поскольку сводится к эквивалентному квадратному уравнению c_{1}(d_{i+1}-\lambda)+c_{2}(d_{i}-\lambda)+c_{3}(d_{i}-\lambda)(d_{i+1}-\lambda)=0
Пусть \lambda_{j} - приближённое значение корня. определим c_{1},c_{2} и c_{3} так, чтобы \frac{c_{1}}{d_{i}-\lambda} + \frac{c_{2}}{d_{i+1}-\lambda} + c_{3} = h(\lambda) \approx f(\lambda) = 1 + \rho \sum_{k=1, n} \frac{u_{k}^{2}} {d_{k}-\lambda} для \lambda в окрестности \lambda_{j}. Заметим, что f(\lambda) = 1 + \rho \sum_{k=1, i} \frac{u_{k}^{2}} {d_{k}-\lambda} + \rho \sum_{k=i+1, n} \frac{u_{k}^{2}} {d_{k}-\lambda} \equiv 1 + \psi_{1}(\lambda) + \psi_{2}(\lambda).
Если \lambda \in (d_{i+1},d_{i}), то \psi_{1}(\lambda) есть сумма положительных слагаемых, а \psi_{2}(\lambda) - сумма отрицательных. Поэтому и \psi_{1}(\lambda), и \psi_{2}(\lambda) могут быть вычислены с высокой точностью; однако при их сложении вполне вероятно взаимное уничтожение верных разрядов и потеря относительной точности в сумме. Возьмем числа c_{1} и \hat{c_{1}}, такие, что функция h_{1}(\lambda) \equiv \hat{c_{1}} + \frac{c_{1}}{d_{i}-\lambda} удовлетворяет условиям h_{1}(\lambda_{j}) = \psi_{1}(\lambda_{j}) и h_{1}^{'}(\lambda_{j})=\psi_{1}^{'}(\lambda_{j}) (*)
Это означает, что гипербола, являющаяся графиком функции h_{1}(\lambda), касается графика функции \psi_{i}(\lambda) при \lambda = \lambda_{j}. Два условия в (*) - это обычные условия метода Ньютона, за исключением того, что вместо прямой в качестве приближения используется гипербола. Легко проверить, что c_{1}=\psi_{1}^{'}(\lambda_{j})(d_{i} - \lambda_{j})^{2} и \hat{c_{1}}=\psi_{1}(\lambda_{j}) - \psi_{1}^{'}(\lambda_{j})(d_{i} - \lambda_{j}).
Подобным же образом выбираем c_{2} и \hat{c_{2}} так, чтобы функция h_{2}(\lambda) \equiv \hat{c_{2}} + \frac{c_{2}}{d_{i+1}-\lambda} удовлетворяла условиям h_{2}(\lambda_{j}) = \psi_{2}(\lambda_{j}) и h_{2}^{'}(\lambda_{j})=\psi_{2}^{'}(\lambda_{j})
Наконец, полагаем h(\lambda) = 1 + h_{1}(\lambda) + h_{2}(\lambda) = (1 + \hat{c_{1}} + \hat{c_{2}} + \frac{c_{1}}{d_{i}-\lambda} + \frac{c_{2}}{d_{i+1}-\lambda} \equiv c_{3} + \frac{c_{1}}{d_{i}-\lambda} + \frac{c_{2}}{d_{i+1}-\lambda}.
1.3 Вычислительное ядро алгоритма
Вычислительным ядром последовательной схемы решения будет являться вычисление матрицы Q собственных векторов при помощи умножения матрицы Q = \begin{bmatrix} Q_{1} & 0 \\ 0 & Q_{2}\end{bmatrix} на матрицу Q^{'}. Эта операция имеет сложность cn^{3} о чём будет говориться ниже, в разделе #Последовательная сложность алгоритма .
Данной операции предшествует вычисление собственных значений и векторов матрицы D + \rho uu^{T}.
1.4 Макроструктура алгоритма
В разделе #Информационный граф описана структура алгоритма, в которой есть блок умножения матриц для вычисления собственных векторов, являющийся вычислительным ядром алгоритма. В соответствующем разделе (#Вычислительное ядро алгоритма) мы упоминали о том, что данному блоку предшествует вычисление собственных значений, которое производится методом Ньютона.
1.5 Схема реализации последовательного алгоритма
Рассмотрим каким именно образом происходит вычисление собственных значений и собственных векторов симметричной трехдиагональной матрицы при помощи стратегии "разделяй и властвуй":
proc dc_eig(T,Q,\Lambda)... по входной матрице T вычисляются выходные матрицы Q и \Lambda, такие, что T = Q\Lambda Q^{T}
В случае, если T - матрица размера 1 x 1 :
1. Присвоить выходным параметрам значения Q = 1, \Lambda = T
Иначе:
1. Представить T в виде T = \begin{bmatrix} T_{1} & 0 \\ 0 & T_{2}\end{bmatrix} + b_{m}vv^{T}
2. call dc_eig(T_{1},Q_{1},\Lambda_{1})
3. call dc_eig(T_{2},Q_{2},\Lambda_{2})
4. Построить D+\rho uu^{T} по \Lambda_{1},\Lambda_{2}, Q_{1}, Q_{2}
5. Найти матрицу собственных значений \Lambda
6. Найти матрицу собственных векторов Q^{'} для матрицы D+\rho uu^{T}
7. Построить матрицу собственных векторов Q для матрицы T : Q = \begin{bmatrix} Q_{1} & 0 \\ 0 & Q_{2}\end{bmatrix}* Q^{'}
8. Присвоить выходным параметрам значения Q и \Lambda
endif
1.6 Последовательная сложность алгоритма
Рассмотрим сложность алгоритма. Пусть t(n) - число флопов, которое потребуется при обработке матрицы размера n * n процедурой dc_eig. В таком случае
[math] t(n) = 2t(n/2) [/math] два рекурсивных обращения к dc_eig[math](T_{i},Q_{i},\Lambda_{i})[/math] [math] +O(n^{2})[/math] вычисление собственных значений матрицы [math]D+\rho uu^{T}[/math] [math] +O(n^{2})[/math] вычисление собственных векторов матрицы [math]D+\rho uu^{T}[/math] [math] +c*n^{3}[/math] вычисление матрицы [math]Q = \begin{bmatrix} Q_{1} & 0 \\ 0 & Q_{2}\end{bmatrix}*Q^{'}[/math]
Если Q_{1}, Q_{2} и Q^{'} рассматривать как плотные матрицы и использовать стандартный алгоритм матричного умножения, то константа c в последней строке будет равна 1. Следовательно, именно это умножение и будет составлять наиболее трудоёмкую часть алгоритма в целом. Игнорируя члены порядка n^{2}, получаем t(n) = 2t(n/2) + cn^{3}. Решив это разностное уравнение, находим t \approx c\frac{4}{3}n^{3}
На практике константа c обычно оказывается гораздо меньше 1, так как матрица Q^{'} весьма разрежена вследствие явления, которое называется дефляцией, и которое было описано выше.
1.7 Информационный граф
На рисунке 3 изображена структура алгоритма.
Операции:
D - операция Divide разделения матрицы T на матрицы T_{1} и T_{2}
Индексы - размерность
S_{k} - операция Conquer сбора матрицы D
L_{k} - операция поиска собственных значений
S^{'} - операция поиска собственных векторов матрицы Q^{'}
S - операция поиска собственных векторов матрицы Q
1.8 Ресурс параллелизма алгоритма
В структуре алгоритма имеем два параллельных блока - вызов рекурсивных функций dc_eig для вычисления собственных значений и векторов матриц T_{1} и T_{2} - это единственная часть алгоритма, в которой возможно использовать параллелизм.
Рекурсивное разделение матрицы ведёт к иерархии вычислительных подблоков с графом зависимости данных, который принимает вид двоичного дерева. Такая структура является естественным путем разделения вычислений между процессорами.
- В вершине дерева все процессы взаимодействуют.
- В каждой ветви дерева вычисление делится на два вычислительных подблока, внутри каждого из которых процессы параллельно взаимодействуют.
- В листьях деревьев каждый процесс занимается вычислением независимо.
В случае реализации без параллелизма, функции dc_eig отрабатывают последовательно - сначала со входными параметрами T_{1}, Q_{1}, \Lambda_{1}, затем - T_{2}, Q_{2}, \Lambda_{2}.
Таким образом, благодаря параллелизму высота алгоритма параллельного составляет log_{2}(n), тогда как при последовательной реализации высота алгоритма равна сумме геометрической прогрессии 1+2+4+8+...+2^{n-1} = 2^{n} - 1, что значительно сокращает число итераций алгоритма.
Поскольку функции являются рекурсивными, их параллельный вызов даст значительный выигрыш во времени.
При размерности матрицы больше 3 параллельная реализация позволяет сократить количество этапов работы алгоритма больше, чем в два раза.
1.9 Входные и выходные данные алгоритма
Входные данные: трёхдиагональная симметрическая матрица, описанная в разделе #Математическое описание алгоритма.
L = \begin{bmatrix} a_{1} & b_{1}&&&&& \\ b_{1} & \ddots & \ddots \\ & \ddots & a_{m-1} & b_{m-1} \\ && b_{m-1} & a_{m} & b_{m} \\ &&& b_{m} & a_{m+1} & b_{m+1} \\ &&&& b_{m+1} & \ddots \\ &&&&&& \ddots & b_{n-1} \\ &&&&&& b_{n-1} & a_{n} \\ \end{bmatrix}
Объём входных данных: 2n + 1 (в силу симметричности достаточно хранить только диагональ и над/под диагональные элементы).
Выходные данные: Вектор собственных значений длины n и n собственных векторов длины n , соответствующих собственным значениям исходной матрицы.
Объём выходных данных: n(n + 1)
1.10 Свойства алгоритма
Данный алгоритм является самым быстрым алгоритмом среди существующих: Разделяй и властвуй, QR, Бисекция и обратная итерация.
Последовательная сложность данного алгоритма: t = c\frac{4}{3}n^{3}
Она удовлетворяет соотношению t(n) = n^3 +2t(\frac{n}{2})
Параллельная сложность алгоритма (за счет дефляции): O(n^{2.3}); в крайне редких случаях: O(n^{2}) .
Особенности алгоритма:
1. Дефляция (#Дефляция)
2. Адаптированный метод Ньютона (#Макроструктура алгоритма)
2 Программная реализация алгоритма
Вторая часть описания алгоритмов в рамках AlgoWiki рассматривает все составные части процесса их реализации. Рассматривается как последовательная реализация алгоритма, так и параллельная. Описывается взаимосвязь свойств программ, реализующих алгоритм, и особенностей архитектуры компьютера, на которой они выполняются. Исследуется работа с памятью, локальность данных и вычислений, описывается масштабируемость и эффективность параллельных программ, производительность компьютеров, достигаемая на данной программе. Обсуждаются особенности реализации для разных классов архитектур компьютеров, приводятся ссылки на реализации в существующих библиотеках.
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
Тестирование реализации алгоритма проводилось на суперкомпьютере "Ломоносов" с использованием 1, 2, 4, 8, 16 процессоров на матрицах размера от 4 до 4096. Реализация произведена на библиотеке OpenMP.
Общая эффективность программы увеличивается при увеличении числа процессоров (за счет сокращения времени работы программы) и уменьшается при увеличении размера матрицы (за счет увеличения времени обработки входных данных). При одновременном увеличении числа процессоров и размерности матрицы общая эффективность падает.
Ниже приведена схема зависимости времени работы программы от размера матрицы при разном числе процессоров. При размере матрицы от 4 до 1024 время работы очень мало, поэтому эти данные не указаны на схеме.
Параметры компиляции и запуска:
ssh compiler module add slurm module add openmpi/1.5.5-icc g++ _scratch/DivideAndConquer.c++ -fopenmp -std=c++0x -o DC sbatch -p test -n1 run ./DC
Код реализации: https://drive.google.com/open?id=0B0G2UV7cuLwHQk9xd1lyeDNJOXc
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
Единственный найденный пример реализации описан в Francoise Tisseury, Jack Dongarra, "Parallelizing the Divide and Conquer Algorithm for the Symmetric Tridiagonal Eigenvalue Problem on Distributed Memory Architectures" ([3] с. 7, 19-20).
3 Литература
[1] Дж. Деммель, «Вычислительная линейная алгебра» //С. 230-235