Участник:Kosean97/Метод встречи посередине в решении задачи дискретного логарифмирования в группе точек эллиптической кривой: различия между версиями
Kosean97 (обсуждение | вклад) |
Kosean97 (обсуждение | вклад) |
||
| (не показано 6 промежуточных версий этого же участника) | |||
| Строка 61: | Строка 61: | ||
== Макроструктура алгоритма == | == Макроструктура алгоритма == | ||
| − | + | Введем следующие макроопераций: | |
| + | *генерация случайной точки, | ||
| + | *сравнение двух точек, | ||
| + | *сортировка точек, | ||
| + | *поиск точки в отсортированном массиве. | ||
| − | + | ''Генерация случайной точки'' осуществляется случайным выбором натурального числа из множества <math>\{1, \dots, r\}</math> с последующим умножением на это число образующего элемента группы.<br> | |
| − | + | Для определения ''сортировки'' и ''поиска'' определим операцию ''сравнения двух точек'' следующим образом: | |
| + | <math>\forall P_1, P_2 \in G \quad (P_1, P_2) \in Less \iff (P_1)_x < (P_2)_x</math>.<br> | ||
| + | Под операцией ''сортировки'' будем понимать быструю сортировку, под операцией ''поиска'' - бинарный поиск. Каждая из операций использует описанную операцию ''сравнения''. | ||
| + | |||
| + | Макроструктура алгоритма представляет из себя последовательное выполнения операций генерации, сравнения и поиска точек. | ||
== Схема реализации последовательного алгоритма == | == Схема реализации последовательного алгоритма == | ||
| Строка 129: | Строка 137: | ||
* 5 ярусов ширины 1. | * 5 ярусов ширины 1. | ||
Таким образом в терминах высоты ЯПФ сложность метода есть <math>O(1)</math>, в терминах ширины - <math>O(size)</math> | Таким образом в терминах высоты ЯПФ сложность метода есть <math>O(1)</math>, в терминах ширины - <math>O(size)</math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== Входные и выходные данные алгоритма == | == Входные и выходные данные алгоритма == | ||
| − | < | + | '''Входные данные:''' <br> |
| + | *<math>G</math> - группа точек эллиптической кривой, представленная простым числом, коэффициентами уравнения кривой, порядком группы, | ||
| + | *<math>Q</math> - образующий элемент указанной группы, | ||
| + | *<math>P</math> - элемент, логарифм которого необходимо найти. | ||
| + | '''Выходные данные:''' <br> | ||
| + | *<math>n</math> - число такое, что <math>nP=Q</math>. | ||
== Свойства алгоритма == | == Свойства алгоритма == | ||
| Строка 159: | Строка 162: | ||
Проведем исследование масштабируемости параллельной реализации алгоритма на суперкомпьютере "Ломоносов" Суперкомпьютерного комплекса Московского университета.<br> | Проведем исследование масштабируемости параллельной реализации алгоритма на суперкомпьютере "Ломоносов" Суперкомпьютерного комплекса Московского университета.<br> | ||
Используемый компилятор: icc version 15.0.0 (gcc version 4.4.7 compatibility). При компиляции используется оптимизация 2 уровня (флаг -O2).<br> | Используемый компилятор: icc version 15.0.0 (gcc version 4.4.7 compatibility). При компиляции используется оптимизация 2 уровня (флаг -O2).<br> | ||
| − | Предложенная реализация написана на языке C++ с использованием библиотек STL, OpenSSL 1.1. | + | Предложенная реализация написана на языке C++ с использованием библиотек STL, OpenSSL 1.1.1-dev и OpenMPI 1.10.2. |
Параметризация задачи заключалась в указании: | Параметризация задачи заключалась в указании: | ||
Текущая версия на 01:26, 4 декабря 2017
Алгоритм: Применение метода встречи посередине в решении задачи дискретного логарифмирования в группе точек эллиптической кривой
Автор описания: Конюхов Сергей
Эллиптическая криптография — раздел криптографии, который изучает асимметричные криптосистемы, основанные на эллиптических кривых над конечными полями. Основное преимущество эллиптической криптографии заключается в том, что на сегодняшний день не известно существование субэкспоненциальных алгоритмов[1] решения задачи дискретного логарифмирования. Использование эллиптических кривых для создания криптосистем было независимо предложено Нилом Коблицем и Виктором Миллером в 1985 году.
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
Задача дискретного логарифмирования[2] в общем виде заключается в поиске решения g^x=a в некоторой конечной абелевой группе G.
Мы же рассмотрим группу точек эллиптической кривой над полем {\mathbb Z}_p характеристики p \gt 3:
E( {\mathbb Z}_p ) = {\mathcal O} \cup \{ (x, y) \in {\mathbb Z}_p^2 \enspace|\enspace y^2 \equiv x^3 + Ax + B \enspace (mod \thinspace p) \}, где A, B \in {\mathbb Z}_p - константы, удовлетворяющие условию 4A^3+27B^2 \ne 0 \enspace (mod \thinspace p).
В качестве группы G возьмём циклическую подгруппу группы E( {\mathbb Z}_p ) порождённую элементом Q, то есть G=\langle Q \rangle.
Стоит отметить, что группа G является аддитивной, и задачу DLOG стоит переформулировать: в уравнении nQ=P требуется найти n.
1.1 Общее описание алгоритма
Метод "встречи посередине"[3] является вероятностным и основан на так называемом парадоксе дней рождений - для того, чтобы при выборке с возвратом из множества мощности r получить совпадение двух элементов с достаточно большой вероятностью, требуется произвести \sqrt{r} попыток.
Eсли мы найдем совпадение точек вида: lQ = kP, то мы можем получить решение задачи как n=lk^{-1}\enspace (mod \thinspace r).
1.2 Математическое описание алгоритма
G = \langle Q \rangle, |G| = r - циклическая подгруппа группы точек эллиптической кривой. Уравнение nQ = P.
Дано: E, Q, P, r - эллиптическая кривая, образующая группы G, логарифмируемый элемент, порядок группы.
Найти: n - искомый логарифм.
Алгоритм:
- Случайно выбрать \sqrt{r} чисел l_i \in {\mathbb Z}_r и сохранить точки вида l_iQ.
- Отсортировать полученные на предыдущем этапе точки по координате x.
- Для случайных k_j \in {\mathbb Z}_r вычислить точки k_jP и осуществить поиск на совпадение в сохранённом массиве.
- В случае успеха вычислить n=l_ik_j^{-1}\enspace (mod \thinspace r). В случае провала перейти к пункту 3.
1.3 Вычислительное ядро алгоритма
В описываемом алгоритме присутствует три вычислительных ядра: генерация базы данных, сортировка базы данных для дальнейшего поиска, генерация случайных точек - степеней изучаемой точки и поиск совпадений в созданной базе данных.
- Генерация базы данных.
Выбирается некоторый "квант" - число точек - степеней образующей, которые будут генерироваться за одну итерацию. До тех пор пока не наберётся достаточное количество точек, генерируем "квант" случайных точек. Генерация точек осуществляется следующим образом: выбирается псевдослучайное число, после чего образующая умножается на него. - Сортировка базы данных.
Полученная база точек - степеней образующей сортируется по икс-координате (точка А больше точки Б, если икс-координата точки А больше икс-координаты точки Б). Алгоритм сортировки, например, быстрая сортировка. - Генерация и поиск.
Генерируется "квант" точек - степеней изучаемой точки. После чего производится поиск в базе данных точки, обладающую той же икс-координатой, что и выбранная. Поиск осуществляется, например, бинарным поиском.
1.4 Макроструктура алгоритма
Введем следующие макроопераций:
- генерация случайной точки,
- сравнение двух точек,
- сортировка точек,
- поиск точки в отсортированном массиве.
Генерация случайной точки осуществляется случайным выбором натурального числа из множества \{1, \dots, r\} с последующим умножением на это число образующего элемента группы.
Для определения сортировки и поиска определим операцию сравнения двух точек следующим образом:
\forall P_1, P_2 \in G \quad (P_1, P_2) \in Less \iff (P_1)_x \lt (P_2)_x.
Под операцией сортировки будем понимать быструю сортировку, под операцией поиска - бинарный поиск. Каждая из операций использует описанную операцию сравнения.
Макроструктура алгоритма представляет из себя последовательное выполнения операций генерации, сравнения и поиска точек.
1.5 Схема реализации последовательного алгоритма
В качестве описания схемы реализации последовательного алгоритма можно привести данный фрагмент программы на языке С++.
int main( int argc, char** argv )
{
// Определяем группу, исследуемый элемент,
// а так же объем базы данных точек и количество точек,
// генерируемых за один раз, цель исследования.
DLogConfig config( "config.txt" );
DLogSolver solver( &argc, &argv, config );
do
{
// Сгенерировать некоторое количество точек - степеней образующей.
solver.GenerateDatabase();
}
// До тех пор, пока нужное количество точек не будет создано.
while( !solver.DatabaseFull() );
// Сортировка полученной базы данных.
solver.PrepareDatabase();
do
{
// Сгенерировать некоторое количество точек - степеней исследуемого элемента.
solver.GeneratePoints();
// Поиск совпадений в базе данных.
solver.LookThrowDatabase();
}
// Повторять до тех пор, пока совпадение не будет найдено.
while( !solver.SolutionFound() );
// Вывести ответ.
solver.PrintAnswer();
return EXIT_SUCCESS;
}
1.6 Последовательная сложность алгоритма
Будем считать генерацию точки за элементарную операцию.
Сложность этапа генерации базы точек есть \sqrt{r}, так как точки хранятся в связном списке, добавление составляет константную сложность.
Сортировка производится алгоритмом Q-Sort, тем самым будет выполнено порядка \sqrt{r}\log r операций. Поиск по созданной базе точек осуществляется алгоритмом бинарного поиска, таким образом, проверка на вхождение нужного элемента производится за \log r операций. Вычисление логарифма по найденной паре выполняется за
константу.
Таким образом:
- временная сложность алгоритма есть O(\sqrt{r}\log r),
- оценка используемой памяти есть O(\sqrt{r}),
где r - это порядок группы G точек эллиптической кривой.
1.7 Информационный граф
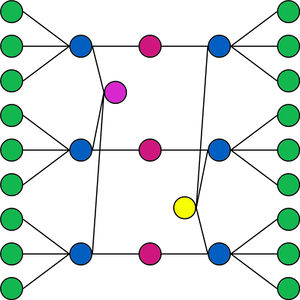
На рисунке 1 можно видеть информационный граф алгоритма дискретного логарифмирования методом встречи посередине. Так, зеленым вершинам соответствует операция случайного выбора точки из группы. Каждая точка сохраняется в один из связных списков, группировка происходит на основании икс-координаты точки. Вершине, отмеченной розовым цветом, соответствует подсчёт общего количества точек. После этого, каждая группа точек по отдельности сортируется. Данному процессу соответствуют вершины, обозначенные красным цветом. Следующим этапом мы генерируем еще одно множество точек, и раздельно, в соответствии с икс-координатой, их сохраняем. Аналогично, этим операциям соответствуют зеленые и синие вершины (справа). В каждой группе из выбранных точек ищется вхождение соответствующего элемента в отсортированном массиве. Желтой вершине соответствует операция, результатом которой есть ответ на вопрос, была ли найдена коллизия.
1.8 Ресурс параллелизма алгоритма
В случае, когда квант точек, генерируемых за одну итерацию, достаточно велик, и за один подход генерируется вся база данных, мы имеем минимальную высоту ЯПФ. Число ярусов в таком случае равно семи (как следствие из Рис. 1). Не нарушая общности q \in {\mathbb N}: q \cdot size = \sqrt{r}, где size - число процессов.
Анализируя ярусно-параллельную форма графа алгоритма, можно выделить:
- 2 яруса ширины \sqrt{r},
- 5 ярусов ширины 1.
Таким образом в терминах высоты ЯПФ сложность метода есть O(1), в терминах ширины - O(size)
1.9 Входные и выходные данные алгоритма
Входные данные:
- G - группа точек эллиптической кривой, представленная простым числом, коэффициентами уравнения кривой, порядком группы,
- Q - образующий элемент указанной группы,
- P - элемент, логарифм которого необходимо найти.
Выходные данные:
- n - число такое, что nP=Q.
1.10 Свойства алгоритма
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
2.4.1 Масштабируемость алгоритма
В параллельном варианте описываемого метода, ось ординат разбивается между процессами на полусегменты равной длины, и каждому процессу, в зависимости от его номера, отводится свой полусегмент. Каждый процесс на этапе генерации базы данных, состоящей из точек на эллиптической кривой, определяет, какому процессу соответствует данная точка, и после того, как было создано некоторое количество точек, происходит пересылка каждого процесса с каждым. Взаимодействие осуществляется по принципу кругового турнира.
На этапе поиска коллизии происходит обмен точками по такому же принципу так, чтобы каждый процесс искал совпадение среди точек своего полусегмента.
2.4.2 Масштабируемость реализации
Проведем исследование масштабируемости параллельной реализации алгоритма на суперкомпьютере "Ломоносов" Суперкомпьютерного комплекса Московского университета.
Используемый компилятор: icc version 15.0.0 (gcc version 4.4.7 compatibility). При компиляции используется оптимизация 2 уровня (флаг -O2).
Предложенная реализация написана на языке C++ с использованием библиотек STL, OpenSSL 1.1.1-dev и OpenMPI 1.10.2.
Параметризация задачи заключалась в указании:
- числа задействованных процессов (2, 4, 8, 16, 32, 64, 128),
- количества бит, необходимых для представления простого числа - параметра исследуемой группы (16, 20, 24, 28, 32, 36, 40).
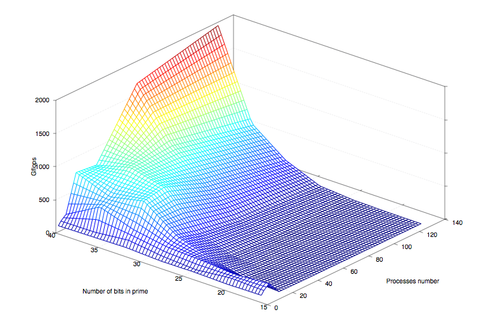
Каждое простое число генерировалось случайно и один раз. Для каждого простого числа коэффициенты эллиптической кривой генерировались случайно и один раз. При каждом запуске использовался один и тот же образующий элемент, и каждый раз логарифм считался для фиксированной точки. Количество точек, которые генерировались за одну итерацию, было выбрано так, чтобы 128 процессов завершили этап генерации базы данных точек за один подход.
На графике видно, что для групп меньшей мощности для достижения оптимального времени работы достаточно меньшего количества процессов. Для групп малого размера, накладные расходы, возникающие при синхронизации процессов, ведут к ухудшению производительности. По мере увеличения порядка группы, и увеличения тем самым количества точек для сортировки и поиска, увеличивается и количество процессов, необходимых для достижения оптимального времени работы алгоритма. Эта "диагональ" явно отображена в графической интерпретации проведенных экспериментов.
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
В связи с тем, что данный метод имеет сугубо академический характер, широкоизвестных реализаций не существует. Главная проблема данного алгоритма заключается в том, что затраты по памяти составляют \sqrt{|G|}. В частности, если взять эллиптическую кривую наименьшего порядка из тех, что могли бы использоваться в приложениях, потребуется хранить в оперативной памяти вычислительного комплекса более чем терабайт данных.
3 Литература
- ↑ Василенко О.Н. Теоретико-числовые алгоритмы в криптографии. Изд. 2-е. доп. - М.: МЦНМО, 2006. - 336 с.
- ↑ Применко Э.А. Алгебраические основы криптографии: Учебное пособие. Изд. 2-е, испр. - М.: ЛЕНАНД, 2015. - 288 с.
- ↑ Бабенко Л.К., Ищукова Е.А., Сидоров И.Д. Параллельные алгоритмы для решения задач защиты информации. - М.: Горячая линия - Телеком, 2014. - 304 с.