|
|
| (не показано 65 промежуточных версий 10 участников) |
| Строка 1: |
Строка 1: |
| | + | {{algorithm |
| | + | | name = Однокубитное преобразование <br /> вектора-состояния |
| | + | | serial_complexity = <math>3 \cdot 2^n</math> |
| | + | | pf_height = <math>2</math> |
| | + | | pf_width = <math>2^{n+1}</math> |
| | + | | input_data = <math>2^n+4</math> |
| | + | | output_data = <math>2^n</math> |
| | + | }} |
| | | | |
| | + | Основные авторы описания: [[Участник:Chernyavskiy|А.Ю.Чернявский]]. |
| | | | |
| − | == Описание свойств и структуры алгоритма == | + | == Свойства и структура алгоритма == |
| | | | |
| | === Общее описание алгоритма === | | === Общее описание алгоритма === |
| | | | |
| − | Алгоритм производит моделирование действия однокубитного квантового вентиля на вектор-состояние. | + | ''Алгоритм производит моделирование действия однокубитного квантового вентиля на вектор-состояние.'' |
| | + | <ref>[http://sqi.cs.msu.su/store/storage/jpvtv20_algebraic_tools.pdf Кронберг Д. А., Ожигов Ю. И., Чернявский А. Ю. Алгебраический аппарат квантовой информатики.]</ref> |
| | + | <ref>[http://sqi.cs.msu.su/files/book_v01.pdf Корж О. В., Чернявский А. Ю. Практикум по суперкомпьютерным технологиям и квантовым вычислениям 3 курс.] </ref> |
| | + | <ref>Preskill J. Lecture notes for physics 229: Quantum information and computation //California Institute of Technology. – 1998.</ref> |
| | + | <ref>Нильсен М., Чанг И. Квантовые вычисления и квантовая информация. – М : Мир, 2006.</ref> |
| | + | Данный алгоритм обычно является подпрограммой и многократно применяется к различным кубитам одного состояния (например при моделировании квантовых алгоритмов или анализе квантовой запутанности). Особенностью алгоритма, как и большинства алгоритмов квантовой инфоорматики, является экспоненциальный рост объема данных в зависимости от основного параметра - числа кубитов, что приводит к необходимости суперкомпьютерной реализации для решения важных практических задач. |
| | | | |
| − | ==== Математическая формулировка ==== | + | === Математическое описание алгоритма === |
| − | Состояние <math>n</math> кубитов задается комплексным вектором <math>v</math> размерности <math>2^n.</math> Однокубитная операция задается унитарной матрицей <math>U</math> размера <math>2 \times 2.</math> Состояние после действия преобразования <math>U</math> на <math>k-</math>й кубит имеет вид <math>v_{out} = I_{2^{k-1}}\otimes U \otimes I_{2^{n-k}},</math> где <math>I_{j} - </math> единичная матрица размерности <math>j,</math> а <math>\otimes - </math> тензорное произведение (произведение Кронекера).
| |
| | | | |
| − | === Математическое описание ===
| + | '''Исходные данные:''' |
| | | | |
| − | Исходные данные: положительно определённая симметрическая матрица <math>A</math> (элементы <math>a_{ij}</math>).
| + | Целочисленные параметры <math>n - </math> число кубитов (необязательно) и <math>k -</math> номер кубита, над которым производится преобразование. |
| | | | |
| − | Вычисляемые данные: левая треугольная матрица <math>L</math> (элементы <math>l_{ij}</math>).
| + | Комплексная матрица <math>U = \begin{pmatrix} |
| | + | u_{00} & u_{01}\\ |
| | + | u_{10} & u_{11} |
| | + | \end{pmatrix}</math> однокубитного преобразования размера <math>2 \times 2.</math> |
| | | | |
| − | Формулы метода:
| + | Комплексный вектор <math>v</math> размерности <math>2^n,</math> задающий начальное состояние многокубитной системы. |
| − | :<math>
| |
| − | \begin{align}
| |
| − | l_{11} & = \sqrt{a_{11}}, \\
| |
| − | l_{j1} & = \frac{a_{j1}}{l_{11}}, \quad j \in [2, n], \\
| |
| − | l_{ii} & = \sqrt{a_{ii} - \sum_{p = 1}^{i - 1} l_{ip}^2}, \quad i \in [2, n], \\
| |
| − | l_{ji} & = \left (a_{ji} - \sum_{p = 1}^{i - 1} l_{ip} l_{jp} \right ) / l_{ii}, \quad i \in [2, n - 1], j \in [i + 1, n].
| |
| − | \end{align}
| |
| − | </math> | |
| | | | |
| − | Существует также блочная версия метода, однако в данном описании разобран только точечный метод.
| |
| | | | |
| − | В ряде реализаций деление на диагональный элемент выполняется в два этапа: вычисление <math>\frac{1}{l_{ii}}</math> и затем умножение на него всех (видоизменённых) <math>a_{ji}</math> . Здесь мы этот вариант алгоритма не рассматриваем. Заметим только, что он имеет худшие параллельные характеристики, чем представленный.
| + | '''Вычисляемые данные:''' комплексный вектор <math>w</math> размерности <math>2^n,</math> соответствующий состоянию после преобразования. |
| | | | |
| − | === Вычислительное ядро алгоритма ===
| |
| | | | |
| − | Вычислительное ядро последовательной версии метода Холецкого можно составить из множественных (всего их <math>\frac{n (n - 1)}{2}</math>) вычислений скалярных произведений строк матрицы:
| + | '''Формулы метода:''' |
| | | | |
| − | :<math>\sum_{p = 1}^{i - 1} l_{ip} l_{jp}</math>
| + | Состояние после действия преобразования <math>U</math> на <math>k-</math>й кубит имеет вид <math>v_{out} = I_{2^{k-1}}\otimes U \otimes I_{2^{n-k}},</math> где <math>I_{j} - </math> единичная матрица размерности <math>j,</math> а <math>\otimes - </math> тензорное произведение (произведение Кронекера). |
| | | | |
| − | в режиме накопления или без него, в зависимости от требований задачи. В отечественных реализациях, даже в последовательных, упомянутый способ представления не используется. Дело в том, что даже в этих реализациях метода вычисление сумм типа
| + | Однако, элементы итогового вектора можно записать и в прямом виде, что более удобно для вычислений: |
| | | | |
| − | :<math>a_{ji} - \sum_{p = 1}^{i - 1} l_{ip} l_{jp}</math><nowiki/> | + | :<math> |
| | + | w_{i_1i_2\ldots i_k \ldots i_n} = \sum\limits_{j_k=0}^1 u_{i_k j} v_{i_1i_2\ldots j_k \ldots i_n} = u_{i_k 0} v_{i_1i_2\ldots 0_k \ldots i_n} + u_{i_k 1} v_{i_1i_2\ldots 1_k \ldots i_n} |
| | + | </math> |
| | | | |
| − | в которых и встречаются скалярные произведения, ведутся не в порядке «вычислили скалярное произведение, а потом вычли его из элемента», а путём вычитания из элемента покомпонентных произведений, являющихся частями скалярных произведений. Поэтому следует считать вычислительным ядром метода не вычисления скалярных произведений, а вычисления выражений | + | Индекс-кортеж <math>i_1i_2\ldots i_n</math> представляет собой двоичную запись индекса элемента в массиве. |
| | | | |
| − | :<math>a_{ji} - \sum_{p = 1}^{i - 1} l_{ip} l_{jp}</math>
| + | === Вычислительное ядро алгоритма === |
| | | | |
| − | в ''режиме накопления'' или без него.
| + | Вычислительное ядро алгоритма представляет собой независимое вычисление всех <math>2^n</math> элементов вектора <math>w.</math> Вычисление каждого элемента требует две операции умножения и одну операцию сложения. Кроме того необходимо вычислять индексы типа <math>i_1i_2\ldots 0_k \ldots i_n,</math> а также значение бита <math>i_k,</math> что требует побитовых операций. |
| − | | |
| − | Тем не менее, в популярных зарубежных реализациях точечного метода Холецкого, в частности, в библиотеках LINPACK и LAPACK, основанных на BLAS, используются именно вычисления скалярных произведений в виде вызова соответствующих подпрограмм BLAS (конкретно — функции SDOT). На последовательном уровне это влечёт за собой дополнительную операцию суммирования на каждый из <math>\frac{n (n + 1)}{2}</math> вычисляемый элемент матрицы <math>L</math> и некоторое замедление работы программы (о других следствиях рассказано ниже в разделе «[[#Существующие реализации алгоритма|Существующие реализации алгоритма]]»). Поэтому в данных вариантах ядром метода Холецкого будут вычисления этих скалярных произведений.
| |
| | | | |
| | === Макроструктура алгоритма === | | === Макроструктура алгоритма === |
| | + | Как записано и в [[#Вычислительное ядро алгоритма|описании ядра алгоритма]], основную часть метода составляют независимые вычсиления элементов выходного вектора. |
| | | | |
| − | Как записано и в [[#Вычислительное ядро алгоритма|описании ядра алгоритма]], основную часть метода составляют множественные (всего <math>\frac{n (n - 1)}{2}</math>) вычисления сумм
| + | === Схема реализации последовательного алгоритма === |
| − | | + | Для индекса <math>i</math> от <math>0</math> до <math>2^n-1</math> |
| − | :<math>a_{ji}-\sum_{p=1}^{i-1}l_{ip} l_{jp}</math>
| + | #Вычислить элемент <math>i_k</math> двоичного представления индекса <math>i.</math> |
| − | | + | #Вычислить индексы <math>j</math> имеющие двоичные представления <math>i_1i_2\ldots \overline{i_k} \ldots i_n,</math> где крышка означает обращение бита. |
| − | в режиме накопления или без него.
| + | #Вычислить <math>w_i = u_{i_k i_k}\cdot v_{i} + u_{i_k \overline{i_k}}\cdot v_j.</math> |
| − | | |
| − | === Описание схемы реализации последовательного алгоритма === | |
| − | | |
| − | Последовательность исполнения метода следующая:
| |
| − | | |
| − | 1. <math>l_{11}= \sqrt{a_{11}}</math>
| |
| − | | |
| − | 2. <math>l_{j1}= \frac{a_{j1}}{l_{11}}</math> (при <math>j</math> от <math>2</math> до <math>n</math>).
| |
| − | | |
| − | Далее для всех <math>i</math> от <math>2</math> до <math>n</math> по нарастанию выполняются
| |
| − | | |
| − | 3. <math>l_{ii} = \sqrt{a_{ii} - \sum_{p = 1}^{i - 1} l_{ip}^2}</math> и
| |
| − | | |
| − | 4. (кроме <math>i = n</math>): <nowiki/><math>l_{ji} = \left (a_{ji} - \sum_{p = 1}^{i - 1} l_{ip} l_{jp} \right ) / l_{ii}</math> (для всех <math>j</math> от <math>i + 1</math> до <math>n</math>).
| |
| − | | |
| − | После этого (если <math>i < n</math>) происходит переход к шагу 3 с бо́льшим <math>i</math>.
| |
| − | | |
| − | Особо отметим, что вычисления сумм вида <math>a_{ji} - \sum_{p = 1}^{i - 1} l_{ip} l_{jp}</math> в обеих формулах производят в режиме накопления вычитанием из <math>a_{ji}</math> произведений <math>l_{ip} l_{jp}</math> для <math>p</math> от <math>1</math> до <math>i - 1</math>, c нарастанием <math>p</math>.
| |
| | | | |
| | === Последовательная сложность алгоритма === | | === Последовательная сложность алгоритма === |
| − | | + | Алгоритм требует: |
| − | Для разложения матрицы порядка n методом Холецкого в последовательном (наиболее быстром) варианте требуется:
| + | # <math>2^{n+1}</math> операций умножения комплексных чисел; |
| − |
| + | # <math>2^n</math> операций сложения комплексных чисел; |
| − | * <math>n</math> вычислений квадратного корня,
| + | # <math>2^n</math> операций получения значения <math>k</math>-го бита числа; |
| − | * <math>\frac{n(n-1)}{2}</math> делений,
| + | # <math>2^n</math> операций изменения значения <math>k</math>-го бита числа. |
| − | * по <math>\frac{n^3-n}{6}</math> умножений и сложений (вычитаний) — ''основная часть алгоритма''.
| + | Отметим, что данный алгоритм обычно применяется много раз подряд, в связи с чем вычисления, связанные с побитовыми операциями (3-4), могут однократно проводиться в начале алгоритма. Кроме того, от них можно избавиться, пользуясь сложением и логическим умножением с числом <math>2^k,</math> которое сохраняется для всего алгоритма. |
| − |
| |
| − | При этом использование режима накопления требует совершения умножений и вычитаний в режиме двойной точности (или использования функции вроде DPROD в Фортране), что ещё больше увеличивает долю умножений и сложений/вычитаний во времени, требуемом для выполнения метода Холецкого.
| |
| − | | |
| − | При классификации по последовательной сложности, таким образом, метод Холецкого относится к алгоритмам ''с кубической сложностью''.
| |
| | | | |
| | === Информационный граф === | | === Информационный граф === |
| | + | Представим рисунки графов алгоритма для случая <math>n=3, k=1</math> (рис.1) и <math>n=3, k=2</math> (рис.2). На графах не представлены матрицы преобразования <math>U,</math> в связи с тем, что их размер при больших <math>n</math> много меньше, нежели размеры входного и выходного векторов. На Рис.3 изображена основная операция, представляемая на Рис.1 и Рис.2 оранжевым цветом. |
| | | | |
| − | Опишем [[глоссарий#Граф алгоритма|граф алгоритма]] как аналитически, так и в виде рисунка.
| + | Отображение графа со входными и выходными данных, а также "свёрнутой" тройной операцией удобно для понимания локальности обращений к памяти. |
| − | | + | Отметим, что структура графа (а именно обращение к входным данным) сильно зависит от параметра <math>k.</math> |
| − | Граф алгоритма состоит из трёх групп вершин, расположенных в целочисленных узлах трёх областей разной размерности.
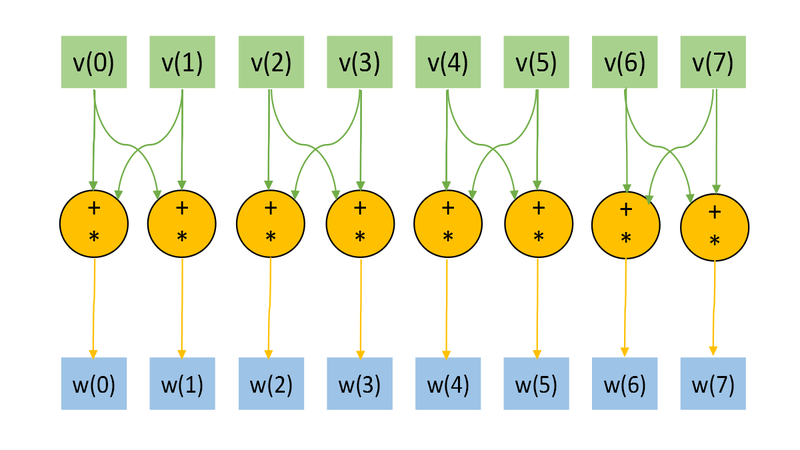
| + | [[file:OneQubitVectorTransform1.png|thumb|center|800px|Рисунок 1. Граф алгоритма для <math>n=3, k=1</math> без отображения матрицы преобразования <math>U.</math> ]] |
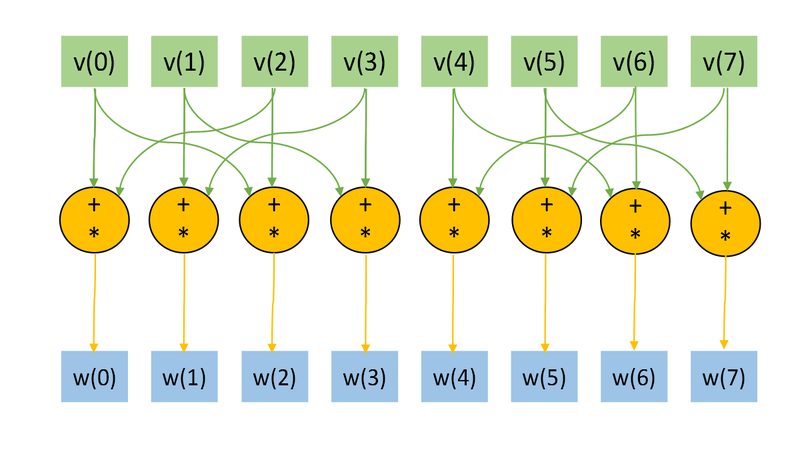
| − | | + | [[file:OneQubitVectorTransform.png|thumb|center|800px|Рисунок 2. Граф алгоритма для <math>n=3, k=2</math> без отображения матрицы преобразования <math>U.</math> ]] |
| − | '''Первая''' группа вершин расположена в одномерной области, соответствующая ей операция вычисляет функцию SQRT.
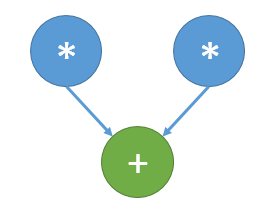
| + | [[file:q_operation.png|thumb|center|300px|Рисунок 3. Граф основной операции.]] |
| − | Естественно введённая единственная координата каждой из вершин <math>i</math> меняется в диапазоне от <math>1</math> до <math>n</math>, принимая все целочисленные значения.
| |
| − | | |
| − | Аргумент этой функции
| |
| − |
| |
| − | * при <math>i = 1</math> — элемент ''входных данных'', а именно <math>a_{11}</math>;
| |
| − | * при <math>i > 1</math> — результат срабатывания операции, соответствующей вершине из третьей группы, с координатами <math>i - 1</math>, <math>i</math>, <math>i - 1</math>.
| |
| − | Результат срабатывания операции является ''выходным данным'' <math>l_{ii}</math>.
| |
| − | | |
| − | '''Вторая''' группа вершин расположена в одномерной области, соответствующая ей операция <math>a / b</math>.
| |
| − | Естественно введённые координаты области таковы:
| |
| − | * <math>i</math> — меняется в диапазоне от <math>1</math> до <math>n-1</math>, принимая все целочисленные значения;
| |
| − | * <math>j</math> — меняется в диапазоне от <math>i+1</math> до <math>n</math>, принимая все целочисленные значения.
| |
| − | | |
| − | Аргументы операции следующие:
| |
| − | *<math>a</math>:
| |
| − | ** при <math>i = 1</math> — элементы ''входных данных'', а именно <math>a_{j1}</math>;
| |
| − | ** при <math>i > 1</math> — результат срабатывания операции, соответствующей вершине из третьей группы, с координатами <math>i - 1, j, i - 1</math>;
| |
| − | * <math>b</math> — результат срабатывания операции, соответствующей вершине из первой группы, с координатой <math>i</math>.
| |
| | | | |
| − | Результат срабатывания операции является ''выходным данным'' <math>l_{ji}</math>.
| + | === Ресурс параллелизма алгоритма === |
| | + | Как видно из информационного графа, прямой алгоритм моделирования однокубитного преобразования обладает высочайшей степенью параллелизма. Все операции вычисления элементов нового вектора-состояния могут быть произведены параллельно. Для вычисления одного элемента необходимо выполнить две операции умножения и одну операцию сложения, операции умножения, в свою очередь, также могут быть выполнены параллельно. |
| | + | Таким образом, необходимо выполнение двух ярусов: одного, состоящего из <math>2^{n+1}</math> умножений и другого, состоящего из <math>2^n</math> сложений. |
| | | | |
| − | '''Третья''' группа вершин расположена в трёхмерной области, соответствующая ей операция <math>a - b * c</math>. | + | === Входные и выходные данные алгоритма === |
| − | Естественно введённые координаты области таковы:
| + | '''Входные данные:''' |
| − | * <math>i</math> — меняется в диапазоне от <math>2</math> до <math>n</math>, принимая все целочисленные значения;
| |
| − | * <math>j</math> — меняется в диапазоне от <math>i</math> до <math>n</math>, принимая все целочисленные значения;
| |
| − | * <math>p</math> — меняется в диапазоне от <math>1</math> до <math>i - 1</math>, принимая все целочисленные значения.
| |
| | | | |
| − | Аргументы операции следующие:
| + | * Комплексный вектор состояния <math>u</math> длины <math>2^n.</math> Обычно нормирован на единицу. |
| − | *<math>a</math>:
| + | * Унитарная матрица <math>U</math> порядка <math>2</math>. |
| − | ** при <math>p = 1</math> элемент входных данных <math>a_{ji}</math>;
| + | * Номер кубита <math>q</math>. |
| − | ** при <math>p > 1</math> — результат срабатывания операции, соответствующей вершине из третьей группы, с координатами <math>i, j, p - 1</math>;
| |
| − | *<math>b</math> — результат срабатывания операции, соответствующей вершине из второй группы, с координатами <math>p, i</math>; | |
| − | *<math>c</math> — результат срабатывания операции, соответствующей вершине из второй группы, с координатами <math>p, j</math>; | |
| | | | |
| − | Результат срабатывания операции является ''промежуточным данным'' алгоритма.
| + | '''Выходные данные:''' |
| | + | * Комплексный вектор состояния <math>w</math> длины <math>2^n</math>. |
| | | | |
| − | Описанный граф можно посмотреть на рисунке, выполненном для случая <math>n = 4</math>. Здесь вершины первой группы обозначены жёлтым цветом и буквосочетанием sq, вершины второй — зелёным цветом и знаком деления, третьей — красным цветом и буквой f. Вершины, соответствующие операциям, производящим выходные данные алгоритма, выполнены более крупно. Дублирующие друг друга дуги даны как одна. На первом изображении показан граф алгоритма согласно классическому определению , на втором к графу алгоритма добавлены вершины , соответствующие входным данным ( обозначены синим цветом ) и выходным данным ( обозначены розовым цветом ).
| + | '''Объем входных данных:''' <math>2^n+4</math> комплексных чисел и <math>1</math> целочисленный параметр. |
| | | | |
| − | [[file:Cholesky full.png|thumb|center|1400px|Граф алгоритма без отображения входных и выходных данных. SQ - вычисление квадратного корня, F - операция a-bc, Div - деление.]]
| + | '''Объем выходных данных:''' <math>2^n</math> комплексных чисел. |
| − | [[file:Cholesky full_in_out.png|thumb|center|1400px|Граф алгоритма с отображением входных и выходных данных. SQ - вычисление квадратного корня, F - операция a-bc, Div - деление, In - входные данные, Out - результаты.]]
| |
| − | | |
| − | === Описание ресурса параллелизма алгоритма ===
| |
| − | | |
| − | Для разложения матрицы порядка <math>n</math> методом Холецкого в параллельном варианте требуется последовательно выполнить следующие ярусы:
| |
| − | * <math>n</math> ярусов с вычислением квадратного корня (единичные вычисления в каждом из ярусов),
| |
| − | * <math>n - 1</math> ярус делений (в каждом из ярусов линейное количество делений, в зависимости от яруса — от <math>1</math> до <math>n - 1</math>),
| |
| − | * по <math>n - 1</math> ярусов умножений и сложений/вычитаний (в каждом из ярусов — квадратичное количество операций, от <math>1</math> до <math>\frac{n^2 - n}{2}</math>.
| |
| − |
| |
| − | Таким образом, в параллельном варианте, в отличие от последовательного, вычисления квадратных корней и делений будут определять довольно значительную долю требуемого времени. При реализации на конкретных архитектурах наличие в отдельных ярусах [[глоссарий#Ярусно-параллельная форма графа алгоритма|ЯПФ]] отдельных вычислений квадратных корней может породить и другие проблемы. Например, при реализации на ПЛИСах остальные вычисления (деления и тем более умножения и сложения/вычитания) могут быть конвейеризованы, что даёт экономию и по ресурсам на программируемых платах; вычисления же квадратных корней из-за их изолированности приведут к занятию ресурсов на платах, которые будут простаивать большую часть времени. Таким образом, общая экономия в 2 раза, из-за которой метод Холецкого предпочитают в случае симметричных задач тому же методу Гаусса, в параллельном случае уже имеет место вовсе не по всем ресурсам, и главное - не по требуемому времени.
| |
| − | | |
| − | При этом использование режима накопления требует совершения умножений и вычитаний в режиме двойной точности, а в параллельном варианте это означает, что практически все промежуточные вычисления для выполнения метода Холецкого в режиме накопления должны быть двойной точности. В отличие от последовательного варианта это означает увеличение требуемой памяти почти в 2 раза.
| |
| − | | |
| − | При классификации по высоте ЯПФ, таким образом, метод Холецкого относится к алгоритмам ''с линейной сложностью''. При классификации по ширине ЯПФ его сложность будет ''квадратичной''.
| |
| − | | |
| − | === Описание входных и выходных данных ===
| |
| − | | |
| − | '''Входные данные''': плотная матрица <math>A</math> (элементы <math>a_{ij}</math>).
| |
| − | Дополнительные ограничения:
| |
| − | * <math>A</math> – симметрическая матрица, т. е. <math>a_{ij}= a_{ji}, i, j = 1, \ldots, n</math>.
| |
| − | * <math>A</math> – положительно определённая матрица, т. е. для любых ненулевых векторов <math>\vec{x}</math> выполняется <math>\vec{x}^T A \vec{x} > 0</math>.
| |
| − | | |
| − | '''Объём входных данных''': <math>\frac{n (n + 1)}{2}</math> (в силу симметричности достаточно хранить только диагональ и над/поддиагональные элементы). В разных реализациях эта экономия хранения может быть выполнена разным образом. Например, в библиотеке, реализованной в НИВЦ МГУ, матрица A хранилась в одномерном массиве длины <math>\frac{n (n + 1)}{2}</math> по строкам своей нижней части.
| |
| − | | |
| − | '''Выходные данные''': левая треугольная матрица <math>L</math> (элементы <math>l_{ij}</math>).
| |
| − | | |
| − | '''Объём выходных данных''': <math>\frac{n (n + 1)}{2}</math> (в силу треугольности достаточно хранить только ненулевые - диагональ и поддиагональные - элементы). В разных реализациях эта экономия хранения может быть выполнена разным образом. Например, в той же библиотеке, созданной в НИВЦ МГУ, матрица <math>L</math> хранилась в одномерном массиве длины <math>\frac{n (n + 1)}{2}</math> по строкам своей нижней части.
| |
| | | | |
| | === Свойства алгоритма === | | === Свойства алгоритма === |
| | + | Соотношение последовательной и параллельной сложности является ''экспоненциальным'' (эксмпонента переходит в константу). |
| | | | |
| − | Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов, как хорошо видно, является ''квадратичным'' (отношение кубической к линейной).
| + | Вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных – ''константа''. |
| − | | |
| − | При этом вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных – всего лишь ''линейна''.
| |
| − | | |
| − | При этом алгоритм почти полностью детерминирован, это гарантируется теоремой о единственности разложения. Использование другого порядка выполнения ассоциативных операций может привести к накоплению ошибок округления, однако это влияние в используемых вариантах алгоритма не так велико, как, скажем, отказ от использования режима накопления.
| |
| − | | |
| − | Дуги информационного графа, исходящие из вершин, соответствующих операциям квадратного корня и деления, образуют пучки т. н. рассылок линейной мощности (то есть степень исхода этих вершин и мощность работы с этими данными — линейная функция от порядка матрицы и координат этих вершин). При этом естественно наличие в этих пучках «длинных» дуг. Остальные дуги локальны.
| |
| − | | |
| − | Наиболее известной является компактная укладка графа — его проекция на треугольник матрицы, который перевычисляется укладываемыми операциями. При этом «длинные» дуги можно убрать, заменив более дальнюю пересылку комбинацией нескольких ближних (к соседям).
| |
| − | | |
| − | == Программная реализация ==
| |
| | | | |
| | + | == Программная реализация алгоритма == |
| | === Особенности реализации последовательного алгоритма === | | === Особенности реализации последовательного алгоритма === |
| | + | На языке C функцию однокубитного преобразования можно записать следующим образом: |
| | | | |
| − | В простейшем (без перестановок суммирования) варианте метод Холецкого на Фортране можно записать так:
| + | <source lang="C"> |
| − | <source lang="fortran"> | + | void OneQubitEvolution(complexd *in, complexd *out, complexd U[2][2], int nqubits, int q) |
| − | DO I = 1, N
| + | { |
| − | S = A(I,I)
| + | //n - число кубитов |
| − | DO IP=1, I-1
| + | //q - номер кубита для преобразования |
| − | S = S - DPROD(A(I,P), A(I,IP))
| |
| − | END DO
| |
| − | A(I,I) = SQRT (S)
| |
| − | DO J = I+1, N
| |
| − | S = A(J,I)
| |
| − | DO IP=1, I-1
| |
| − | S = S - DPROD(A(I,P), A(J,IP))
| |
| − | END DO
| |
| − | A(J,I) = S/A(I,I)
| |
| − | END DO
| |
| − | END DO
| |
| − | </source>
| |
| − | При этом для реализации режима накопления переменная <math>S</math> должна быть двойной точности.
| |
| | | | |
| − | Для метода Холецкого существует блочная версия, которая отличается от точечной не тем, что операции над числами заменены на аналоги этих операций над блоками; её построение основано на том, что практически все циклы точечной версии имеют тип SchedDo в терминах методологии, основанной на исследовании информационного графа и, следовательно, могут быть расщеплены на составляющие. Тем не менее, обычно блочную версию метода Холецкого записывают не в виде программы с расщеплёнными и переставленными циклами, а в виде программы, подобной реализации точечного метода, в которой вместо соответствующих скалярных операций присутствуют операции над блоками.
| + | int shift = nqubits-q; |
| | + | //Все биты нулевые, кроме соответствующего позиции преобразуемого кубита |
| | + | int pow2q=1<<(shift); |
| | | | |
| − | Для обеспечения локальности работы с памятью представляется более эффективной такая схема метода Холецкого (полностью эквивалентная описанной), когда исходная матрица и её разложение хранятся не в нижнем-левом, а в правом-верхнем треугольнике. Это связано с особенностью размещения массивов в Фортране и тем, что в этом случае вычисления скалярных произведений будут идти с выборкой идущих подряд элементов массива.
| + | int N=1<<nqubits; |
| | + | for (int i=0; i<N; i++) |
| | + | { |
| | + | //Обнуления меняющегося бита |
| | + | int i0 = i & ~pow2q; |
| | + | |
| | + | //Установка меняющегося бита |
| | + | int i1 = i | pow2q; |
| | + | |
| | + | //Получение значения меняющегося бита |
| | + | int iq = (i & pow2q) >> shift; |
| | | | |
| − | Есть и другой вариант точечной схемы: использовать вычисляемые элементы матрицы <math>L</math> в качестве аргументов непосредственно «сразу после» их вычисления. Такая программа будет выглядеть так:
| + | out[i] = U[iq][0] * in[i0] + U[iq][1] *in[i1]; |
| − | <source lang="fortran">
| + | } |
| − | DO I = 1, N
| + | } |
| − | A(I,I) = SQRT (A(I, I)) | |
| − | DO J = I+1, N
| |
| − | A(J,I) = A(J,I)/A(I,I)
| |
| − | END DO
| |
| − | DO K=I+1,N
| |
| − | DO J = K, N
| |
| − | A(J,K) = A(J,K) - A(J,I)*A(K,I)
| |
| − | END DO
| |
| − | END DO
| |
| − | END DO
| |
| | </source> | | </source> |
| − | Как видно, в этом варианте для реализации режима накопления одинарной точности мы должны будем объявить двойную точность для массива, хранящего исходные данные и результат. Подчеркнём, что [[глоссарий#Граф алгоритма|граф алгоритма]] обеих схем - один и тот же (из п.1.7), если не считать изменением замену умножения на функцию DPROD!
| |
| − |
| |
| − | === Описание локальности данных и вычислений ===
| |
| − |
| |
| − | ==== Описание локальности алгоритма ====
| |
| − |
| |
| − | ==== Описание локальности реализации алгоритма ====
| |
| − |
| |
| − | ===== Описание структуры обращений в память и качественная оценка локальности =====
| |
| − |
| |
| − | [[file:Cholesky_locality1.jpg|thumb|center|700px|Рисунок 1. Реализация метода Холецкого. Общий профиль обращений в память]]
| |
| − |
| |
| − | На рисунке 1 представлен профиль обращений в память для реализации метода Холецкого. В программе задействован только 1 массив, поэтому в данном случае обращения в профиле происходят только к элементам этого массива. Программа состоит из одного основного этапа, который, в свою очередь, состоит из последовательности подобных итераций. Пример одной итерации выделен зеленым цветом.
| |
| − |
| |
| − | Видно, что на каждой <math>i</math>-й итерации используются все адреса, кроме первых <math>k_i</math>, при этом с ростом <math>i</math> увеличивается значение <math>k_i</math>. Также можно заметить, что число обращений в память на каждой итерации растет примерно до середины работы программы, после чего уменьшается вплоть до завершения работы. Это позволяет говорить о том, что данные в программе используются неравномерно, при этом многие итерации, особенно в начале выполнения программы, задействуют большой объем данных, что приводит к ухудшению локальности.
| |
| − |
| |
| − | Однако в данном случае основным фактором, влияющим на локальность работы с памятью, является строение итерации. Рассмотрим фрагмент профиля, соответствующий нескольким первым итерациям.
| |
| − |
| |
| − | [[file:Cholesky_locality2.jpg|thumb|center|700px|Рисунок 2. Реализация метода Холецкого. Фрагмент профиля (несколько первых итераций)]]
| |
| − |
| |
| − | Исходя из рисунка 2 видно, что каждая итерация состоит из двух различных фрагментов. Фрагмент 1 – последовательный перебор (с некоторым шагом) всех адресов, начиная с некоторого начального. При этом к каждому элементу происходит мало обращений. Такой фрагмент обладает достаточно неплохой пространственной локальностью, так как шаг по памяти между соседними обращениями невелик, но плохой временно́й локальностью, поскольку данные редко используются повторно.
| |
| − |
| |
| − | Фрагмент 2 устроен гораздо лучше с точки зрения локальности. В рамках этого фрагмента выполняется большое число обращений подряд к одним и тем же данным, что обеспечивает гораздо более высокую степень как пространственной, так и временно́й локальности по сравнению с фрагментом 1.
| |
| − |
| |
| − | После рассмотрения фрагмента профиля на рис. 2 можно оценить общую локальность двух фрагментов на каждой итерации. Однако стоит рассмотреть более подробно, как устроен каждый из фрагментов.
| |
| − |
| |
| − | [[file:Cholesky_locality3.jpg|thumb|center|700px|Рисунок 3. Реализация метода Холецкого. Фрагмент профиля (часть одной итерации)]]
| |
| − |
| |
| − | Рис. 3, на котором представлена часть одной итерации общего профиля, позволяет отметить достаточно интересный факт: строение каждого из фрагментов на самом деле заметно сложнее, чем это выглядит на рис. 2. В частности, каждый шаг фрагмента 1 состоит из нескольких обращений к соседним элементам, причем выполняется не последовательный перебор. Также можно увидеть, что фрагмент 2 на самом деле в свою очередь состоит из повторяющихся итераций, при этом видно, что каждый шаг фрагмента 1 соответствует одной итерации фрагмента 2 (выделено зеленым на рис. 3). Это лишний раз говорит о том, что для точного понимания локальной структуры профиля необходимо его рассмотреть на уровне отдельных обращений.
| |
| − |
| |
| − | Стоит отметить, что выводы на основе рис. 3 просто дополняют общее представлении о строении профиля обращений; сделанные на основе рис. 2 выводы относительно общей локальности двух фрагментов остаются верны.
| |
| − |
| |
| − | ===== Количественная оценка локальности =====
| |
| − |
| |
| − | Первая оценка выполняется на основе характеристики daps, которая оценивает число выполненных обращений (чтений и записей) в память в секунду. Данная характеристика является аналогом оценки flops применительно к работе с памятью и является в большей степени оценкой производительности взаимодействия с памятью, чем оценкой локальности. Однако она служит хорошим источником информации, в том числе для сравнения с результатами по следующей характеристике cvg.
| |
| − |
| |
| − | [[file:Cholesky_locality4.jpg|thumb|center|700px|Рисунок 4. Сравнение значений оценки daps]]
| |
| − |
| |
| − | На рисунке 4 приведены значения daps для реализаций распространенных алгоритмов, отсортированные по возрастанию (чем больше daps, тем в общем случае выше производительность). Можно увидеть, что реализация метода Холецкого характеризуется достаточно высокой скоростью взаимодействия с памятью, однако ниже, чем, например, у теста Линпак или реализации метода Якоби.
| |
| − |
| |
| − | Вторая характеристика – cvg – предназначена для получения более машинно-независимой оценки локальности. Она определяет, насколько часто в программе необходимо подтягивать данные в кэш-память. Соответственно, чем меньше значение cvg, тем реже это нужно делать, тем лучше локальность.
| |
| − |
| |
| − | [[file:Cholesky_locality5.jpg|thumb|center|700px|Рисунок 5. Сравнение значений оценки cvg]]
| |
| − |
| |
| − | На рисунке 5 приведены значения cvg для того же набора реализаций, отсортированные по убыванию (чем меньше cvg, тем в общем случае выше локальность). Можно увидеть, что, согласно данной оценке, реализация метода Холецкого оказалась ниже в списке по сравнению с оценкой daps.
| |
| − |
| |
| − | <!--
| |
| − | ===== Анализ на основе теста Apex-Map =====
| |
| − | --->
| |
| − |
| |
| − | === Возможные способы и особенности реализации параллельного алгоритма ===
| |
| − |
| |
| − | Как нетрудно видеть по структуре графа алгоритма, вариантов распараллеливания алгоритма довольно много. Например, во втором варианте (см. раздел «[[#Особенности реализации последовательного алгоритма|Особенности реализации последовательного алгоритма]]») все внутренние циклы параллельны, в первом — параллелен цикл по <math>J</math>. Тем не менее, простое распараллеливание таким способом «в лоб» вызовет такое количество пересылок между процессорами с каждым шагом по внешнему циклу, которое почти сопоставимо с количеством арифметических операций. Поэтому перед размещением операций и данных между процессорами вычислительной системы предпочтительно разбиение всего пространства вычислений на блоки, с сопутствующим разбиением обрабатываемого массива.
| |
| − |
| |
| − | Многое зависит от конкретного типа вычислительной системы. Присутствие конвейеров на узлах многопроцессорной системы делает рентабельным параллельное вычисление нескольких скалярных произведений сразу. Подобная возможность есть и на программировании ПЛИСов, но там быстродействие будет ограничено медленным последовательным выполнением операции извлечения квадратного корня.
| |
| − |
| |
| − | В принципе, возможно и использование т. н. «скошенного» параллелизма. Однако его на практике никто не использует, из-за усложнения управляющей структуры программы.
| |
| − |
| |
| − | === Масштабируемость алгоритма и его реализации ===
| |
| | | | |
| − | ==== Описание масштабируемости алгоритма ====
| + | Отметим, что существенная часть вычислений и логики кода приходится на битовые операции, однако, этого можно избежать: однокубитное преобразование в большинстве случаев является лишь подпрограммой и применяется к разным кубитам большое число раз. В свою очередь, вычисляемые при помощи битовых операций индексы i0, i1 и iq зависят лишь от параметров количества кубитов n и номера кубита q. Число кубитов обычно фиксировано, соответственно, можно вычислить эти индексы заранее для всех q от 1 до n. Для хранения потребуется лишь массив целочисленных переменных линейного размера 3n в то время, как обрабатываемые данные имеют экспоненциальный размер. Очевидно, что такая оптимизация критически необходима при реализации алгоритма на вычислительных устройствах или языках программирования с отсутствием быстрых битовых операций (примером может служить среда Matlab). |
| | | | |
| − | ==== Описание масштабируемости реализации алгоритма ==== | + | === Возможные способы и особенности параллельной реализации алгоритма === |
| − | Проведём исследование масштабируемости параллельной реализации разложения Холецкого согласно [[Scalability methodology|методике]]. Исследование проводилось на суперкомпьютере "Ломоносов" [http://parallel.ru/cluster Суперкомпьютерного комплекса Московского университета].
| + | Основной способ параллельной реализации очевиден - необходимо распараллеливание основного цикла (параллельное вычисление различных компонент выходного вектора-состояния) и, желательно, операций умножения. На машинах с общей памятью такой вариант распараллеливания приводит к ускорению, близкому к максимально-возможному. |
| | + | Однако, данный способ сталкивается с проблемами локальности данных. Анализируя математическая описание и информационные графы алгоритма легко видеть, что при использовании большого числа узлов с собственной памятью количество необходимых пересылок между узлами становится сопоставимым с количеством вычислений, что приводит к существенной потере эффективности. Возможны разные пути частичного решения этой проблемы, например, кэширование или использование парадигмы программирования SHMEM, однако, столь сильная нелокальность использования данных всё равно не позволяет добиться хорошей эффективности. |
| | | | |
| − | Набор и границы значений изменяемых [[Глоссарий#Параметры запуска|параметров запуска]] реализации алгоритма:
| + | Алгоритм реализован (в основном последовательные версии) в различных библиотеках для квантовой информатики и квантового компьютерного моделирования. Например: QLib, libquantum, QuantumPlayground, LIQUiD. |
| − | | |
| − | * число процессоров [4 : 256] с шагом 4;
| |
| − | * размер матрицы [1024 : 5120].
| |
| − | | |
| − | В результате проведённых экспериментов был получен следующий диапазон [[Глоссарий#Эффективность реализации|эффективности реализации]] алгоритма:
| |
| − | | |
| − | * минимальная эффективность реализации 0,11%;
| |
| − | * максимальная эффективность реализации 2,65%.
| |
| − | | |
| − | На следующих рисунках приведены графики [[Глоссарий#Производительность|производительности]] и эффективности выбранной реализации разложения Холецкого в зависимости от изменяемых параметров запуска.
| |
| − | | |
| − | [[file:Масштабируемость Параллельной реализации метода Холецкого Производительность.png|thumb|center|700px|Рисунок 1. Параллельная реализация метода Холецкого. Изменение производительности в зависимости от числа процессоров и размера матрицы.]]
| |
| − | [[file:Холецкий масштабируемость эффективность.png|thumb|center|700px|Рисунок 2. Параллельная реализация метода Холецкого. Изменение производительности в зависимости от числа процессоров и размера матрицы.]]
| |
| − | | |
| − | Построим оценки масштабируемости выбранной реализации разложения Холецкого:
| |
| − | * По числу процессов: -0,000593. При увеличении числа процессов эффективность на рассмотренной области изменений параметров запуска уменьшается, однако в целом уменьшение не очень быстрое. Малая интенсивность изменения объясняется крайне низкой общей эффективностью работы приложения с максимумом в 2,65%, и значение эффективности на рассмотренной области значений быстро доходит до десятых долей процента. Это свидетельствует о том, что на большей части области значений нет интенсивного снижения эффективности. Это объясняется также тем, что с ростом [[Глоссарий#Вычислительная сложность|вычислительной сложности]] падение эффективности становится не таким быстрым. Уменьшение эффективности на рассмотренной области работы параллельной программы объясняется быстрым ростом накладных расходов на организацию параллельного выполнения. С ростом вычислительной сложности задачи эффективность снижается так же быстро, но при больших значениях числа процессов. Это подтверждает предположение о том, что накладные расходы начинают сильно превалировать над вычислениями.
| |
| − | * По размеру задачи: 0,06017. При увеличении размера задачи эффективность возрастает. Эффективность возрастает тем быстрее, чем большее число процессов используется для выполнения. Это подтверждает предположение о том, что размер задачи сильно влияет на эффективность выполнения приложения. Оценка показывает, что с ростом размера задачи эффективность на рассмотренной области значений параметров запуска сильно увеличивается. Также, учитывая разницу максимальной и минимальной эффективности в 2,5%, можно сделать вывод, что рост эффективности при увеличении размера задачи наблюдается на большей части рассмотренной области значений.
| |
| − | * По двум направлениям: 0,000403. При рассмотрении увеличения как вычислительной сложности, так и числа процессов на всей рассмотренной области значений эффективность увеличивается, однако скорость увеличения эффективности небольшая. В совокупности с тем фактом, что разница между максимальной и минимальной эффективностью на рассмотренной области значений параметров небольшая, эффективность с увеличением масштабов возрастает, но медленно и с небольшими перепадами.
| |
| − | | |
| − | === Динамические характеристики и эффективность реализации алгоритма ===
| |
| − | | |
| − | Для существующих параллельных реализаций характерно отнесение всего ресурса параллелизма на блочный уровень. Относительно низкая эффективность работы связана с проблемами внутри одного узла, следующим фактором является неоптимальное соотношение между «арифметикой» и обменами. Видно, что при некотором (довольно большом) оптимальном размере блока обмены влияют не так уж сильно.
| |
| − | | |
| − | Для проведения экспериментов использовалась реализация разложения Холецкого, представленная в пакете SCALAPACK библиотеки Intel MKL (метод pdpotrf). Все результаты получены на суперкомпьютере «Ломоносов». Использовались процессоры Intel Xeon X5570 с пиковой производительностью в 94 Гфлопс, а также компилятор Intel с опцией –O2.
| |
| − | | |
| − | [[file:Cholesky_efficiency1.jpg|thumb|center|700px]]
| |
| − | | |
| − | На рисунке показана эффективность реализации разложения Холецкого (случай использования нижних треугольников матриц) для разного числа процессов и разной размерности матрицы (10000, 20000 и 50000 элементов). Видно, что общая эффективность достаточно невысока – даже при малом числе процессов менее 10 %. Однако при всех размерностях матрицы эффективность снижается очень медленно – в самом худшем случае, при N = 10000, при увеличении числа процессов с 16 до 900 (в 56 раз) эффективность падает с 7 % до 0,8 % (всего в 9 раз). При N = 50000 эффективность уменьшается еще медленнее.
| |
| − | | |
| − | Также стоит отметить небольшое суперлинейное ускорение, полученное на 4-х процессах для N = 10000 и N = 20000 (для N = 50000 провести эксперименты на таком малом числе процессов не удалось). Помимо более эффективной работы с кэш-памятью, оно, видимо, обусловлено тем, что эти 4 процесса помещаются на ядрах одного процессора, что позволяет использовать общую память, и, соответственно, не приводит к появлению накладных расходов, связанных с пересылкой данных.
| |
| | | | |
| | + | === Результаты прогонов === |
| | === Выводы для классов архитектур === | | === Выводы для классов архитектур === |
| | + | Исходя из высочайшей возможности параллелизации и при этом наличия существенной нелокальности обращения к данным, эффективная и хорошо масштабируемая параллельная реализация алгоритма однокубитного квантового преобразования легко достижима на машинах с общей памятью. Реализация же на машинах с разделяемой памятью имеет низкую эффективность и требует специальных подходов для уменьшения времени работы. Можно отметить, что данная задача является хорошим плацдармом для разработки методов решения задач с интенсивным использованием данных и низкой локальностью. |
| | | | |
| − | Как видно по показателям SCALAPACK на суперкомпьютерах, обмены при большом n хоть и уменьшают эффективность расчётов, но слабее, чем неоптимальность организации расчётов внутри одного узла. Поэтому, видимо, следует сначала оптимизировать не блочный алгоритм, а подпрограммы, используемые на отдельных процессорах: точечный метод Холецкого, перемножения матриц и др. подпрограммы. [[#Существующие реализации алгоритма|Ниже]] содержится информация о возможном направлении такой оптимизации.
| + | == Литература == |
| | | | |
| − | В отношении же архитектуры типа ПЛИС вполне показателен тот момент, что разработчики — наполнители библиотек для ПЛИСов пока что не докладывают об успешных и эффективных реализациях точечного метода Холецкого на ПЛИСах. Это связано со следующим свойством информационной структуры алгоритма: если операции деления или вычисления выражений <math>a - bc</math> являются не только массовыми, но и параллельными, и потому их вычисления сравнительно легко выстраивать в конвейеры, то операции извлечения квадратных корней являются узким местом алгоритма - отведённое на эту операцию оборудование неизбежно будет простаивать большую часть времени. Поэтому для эффективной реализации на ПЛИСах алгоритмов, столь же хороших по вычислительным характеристикам, как и метод квадратного корня, следует использовать не метод Холецкого, а его давно известную модификацию без извлечения квадратных корней — [[Компактная схема разложения Гаусса (вариант для симметричных матриц)|разложение матрицы в произведение <math>L D L^T</math>]].
| + | <references /> |
| − | | |
| − | === Существующие реализации алгоритма ===
| |
| − | | |
| − | Точечный метод Холецкого реализован как в основных библиотеках программ отечественных организаций, так и в западных пакетах LINPACK, LAPACK, SCALAPACK и др.
| |
| − |
| |
| − | При этом в отечественных реализациях, как правило, выполнены стандартные требования к методу с точки зрения ошибок округления, то есть, реализован режим накопления, и обычно нет лишних операций. Правда, анахронизмом в наше время выглядит то, что ряд старых отечественных реализаций использует для экономии памяти упаковку матриц <math>A</math> и <math>L</math> в одномерный массив. При реальных вычислениях на современных вычислительных системах данная упаковка только создаёт дополнительные накладные расходы. Однако отечественные реализации, не использующие такую упаковку, вполне отвечают требованиям современности в отношении вычислительной точности метода.
| |
| − |
| |
| − | Реализация точечного метода Холецкого в современных западных пакетах страдает другими недостатками, вытекающими из того, что все эти реализации, по сути, происходят из одной и той же реализации метода в LINPACK, а та использует пакет BLAS. Основным их недостатком является даже не наличие лишних операций, о котором уже написано в разделе «[[#Вычислительное ядро алгоритма|Вычислительное ядро алгоритма]]», ибо их количество всё же невелико по сравнению с главной частью, а то, что в BLAS скалярное произведение реализовано без режима накопления. Это перечёркивает имеющиеся для метода Холецкого хорошие оценки влияния ошибок округления, поскольку они выведены как раз в предположении использования режима накопления при вычислении скалярных произведений. Поэтому тот, кто использует реализации метода Холецкого из LINPACK, LAPACK, SCALAPACK и т. п. пакетов, серьёзно рискует не получить требуемую вычислительную точность, либо ему придётся для получения хороших оценок ''одинарной точности'' использовать подпрограммы ''двойной''.
| |
| − | | |
| − | == Литература ==
| |
| | | | |
| − | # В.В.Воеводин. Вычислительные основы линейной алгебры. М.: Наука, 1977.
| + | [[Категория:Законченные статьи]] |
| − | # В.В.Воеводин, Ю.А.Кузнецов. Матрицы и вычисления. М.: Наука, 1984.
| + | [[Категория:Алгоритмы моделирования квантовых систем]] |
| − | # Д.К.Фаддеев, В.Н.Фаддева. Вычислительные основы линейной алгебры. М.-Л.: Физматгиз, 1963.
| |
| | | | |
| − | [[en:Cholesky decomposition]] | + | [[En:Single-qubit transform of a state vector]] |
Однокубитное преобразование
вектора-состояния
|
| Последовательный алгоритм
|
| Последовательная сложность
|
[math]3 \cdot 2^n[/math]
|
| Объём входных данных
|
[math]2^n+4[/math]
|
| Объём выходных данных
|
[math]2^n[/math]
|
| Параллельный алгоритм
|
| Высота ярусно-параллельной формы
|
[math]2[/math]
|
| Ширина ярусно-параллельной формы
|
[math]2^{n+1}[/math]
|
Основные авторы описания: А.Ю.Чернявский.
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Алгоритм производит моделирование действия однокубитного квантового вентиля на вектор-состояние.
[1]
[2]
[3]
[4]
Данный алгоритм обычно является подпрограммой и многократно применяется к различным кубитам одного состояния (например при моделировании квантовых алгоритмов или анализе квантовой запутанности). Особенностью алгоритма, как и большинства алгоритмов квантовой инфоорматики, является экспоненциальный рост объема данных в зависимости от основного параметра - числа кубитов, что приводит к необходимости суперкомпьютерной реализации для решения важных практических задач.
1.2 Математическое описание алгоритма
Исходные данные:
Целочисленные параметры [math]n - [/math] число кубитов (необязательно) и [math]k -[/math] номер кубита, над которым производится преобразование.
Комплексная матрица [math]U = \begin{pmatrix}
u_{00} & u_{01}\\
u_{10} & u_{11}
\end{pmatrix}[/math] однокубитного преобразования размера [math]2 \times 2.[/math]
Комплексный вектор [math]v[/math] размерности [math]2^n,[/math] задающий начальное состояние многокубитной системы.
Вычисляемые данные: комплексный вектор [math]w[/math] размерности [math]2^n,[/math] соответствующий состоянию после преобразования.
Формулы метода:
Состояние после действия преобразования [math]U[/math] на [math]k-[/math]й кубит имеет вид [math]v_{out} = I_{2^{k-1}}\otimes U \otimes I_{2^{n-k}},[/math] где [math]I_{j} - [/math] единичная матрица размерности [math]j,[/math] а [math]\otimes - [/math] тензорное произведение (произведение Кронекера).
Однако, элементы итогового вектора можно записать и в прямом виде, что более удобно для вычислений:
- [math]
w_{i_1i_2\ldots i_k \ldots i_n} = \sum\limits_{j_k=0}^1 u_{i_k j} v_{i_1i_2\ldots j_k \ldots i_n} = u_{i_k 0} v_{i_1i_2\ldots 0_k \ldots i_n} + u_{i_k 1} v_{i_1i_2\ldots 1_k \ldots i_n}
[/math]
Индекс-кортеж [math]i_1i_2\ldots i_n[/math] представляет собой двоичную запись индекса элемента в массиве.
1.3 Вычислительное ядро алгоритма
Вычислительное ядро алгоритма представляет собой независимое вычисление всех [math]2^n[/math] элементов вектора [math]w.[/math] Вычисление каждого элемента требует две операции умножения и одну операцию сложения. Кроме того необходимо вычислять индексы типа [math]i_1i_2\ldots 0_k \ldots i_n,[/math] а также значение бита [math]i_k,[/math] что требует побитовых операций.
1.4 Макроструктура алгоритма
Как записано и в описании ядра алгоритма, основную часть метода составляют независимые вычсиления элементов выходного вектора.
1.5 Схема реализации последовательного алгоритма
Для индекса [math]i[/math] от [math]0[/math] до [math]2^n-1[/math]
- Вычислить элемент [math]i_k[/math] двоичного представления индекса [math]i.[/math]
- Вычислить индексы [math]j[/math] имеющие двоичные представления [math]i_1i_2\ldots \overline{i_k} \ldots i_n,[/math] где крышка означает обращение бита.
- Вычислить [math]w_i = u_{i_k i_k}\cdot v_{i} + u_{i_k \overline{i_k}}\cdot v_j.[/math]
1.6 Последовательная сложность алгоритма
Алгоритм требует:
- [math]2^{n+1}[/math] операций умножения комплексных чисел;
- [math]2^n[/math] операций сложения комплексных чисел;
- [math]2^n[/math] операций получения значения [math]k[/math]-го бита числа;
- [math]2^n[/math] операций изменения значения [math]k[/math]-го бита числа.
Отметим, что данный алгоритм обычно применяется много раз подряд, в связи с чем вычисления, связанные с побитовыми операциями (3-4), могут однократно проводиться в начале алгоритма. Кроме того, от них можно избавиться, пользуясь сложением и логическим умножением с числом [math]2^k,[/math] которое сохраняется для всего алгоритма.
1.7 Информационный граф
Представим рисунки графов алгоритма для случая [math]n=3, k=1[/math] (рис.1) и [math]n=3, k=2[/math] (рис.2). На графах не представлены матрицы преобразования [math]U,[/math] в связи с тем, что их размер при больших [math]n[/math] много меньше, нежели размеры входного и выходного векторов. На Рис.3 изображена основная операция, представляемая на Рис.1 и Рис.2 оранжевым цветом.
Отображение графа со входными и выходными данных, а также "свёрнутой" тройной операцией удобно для понимания локальности обращений к памяти.
Отметим, что структура графа (а именно обращение к входным данным) сильно зависит от параметра [math]k.[/math]
Рисунок 1. Граф алгоритма для
[math]n=3, k=1[/math] без отображения матрицы преобразования
[math]U.[/math]
Рисунок 2. Граф алгоритма для
[math]n=3, k=2[/math] без отображения матрицы преобразования
[math]U.[/math]
Рисунок 3. Граф основной операции.
1.8 Ресурс параллелизма алгоритма
Как видно из информационного графа, прямой алгоритм моделирования однокубитного преобразования обладает высочайшей степенью параллелизма. Все операции вычисления элементов нового вектора-состояния могут быть произведены параллельно. Для вычисления одного элемента необходимо выполнить две операции умножения и одну операцию сложения, операции умножения, в свою очередь, также могут быть выполнены параллельно.
Таким образом, необходимо выполнение двух ярусов: одного, состоящего из [math]2^{n+1}[/math] умножений и другого, состоящего из [math]2^n[/math] сложений.
1.9 Входные и выходные данные алгоритма
Входные данные:
- Комплексный вектор состояния [math]u[/math] длины [math]2^n.[/math] Обычно нормирован на единицу.
- Унитарная матрица [math]U[/math] порядка [math]2[/math].
- Номер кубита [math]q[/math].
Выходные данные:
- Комплексный вектор состояния [math]w[/math] длины [math]2^n[/math].
Объем входных данных: [math]2^n+4[/math] комплексных чисел и [math]1[/math] целочисленный параметр.
Объем выходных данных: [math]2^n[/math] комплексных чисел.
1.10 Свойства алгоритма
Соотношение последовательной и параллельной сложности является экспоненциальным (эксмпонента переходит в константу).
Вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных – константа.
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
На языке C функцию однокубитного преобразования можно записать следующим образом:
void OneQubitEvolution(complexd *in, complexd *out, complexd U[2][2], int nqubits, int q)
{
//n - число кубитов
//q - номер кубита для преобразования
int shift = nqubits-q;
//Все биты нулевые, кроме соответствующего позиции преобразуемого кубита
int pow2q=1<<(shift);
int N=1<<nqubits;
for (int i=0; i<N; i++)
{
//Обнуления меняющегося бита
int i0 = i & ~pow2q;
//Установка меняющегося бита
int i1 = i | pow2q;
//Получение значения меняющегося бита
int iq = (i & pow2q) >> shift;
out[i] = U[iq][0] * in[i0] + U[iq][1] *in[i1];
}
}
Отметим, что существенная часть вычислений и логики кода приходится на битовые операции, однако, этого можно избежать: однокубитное преобразование в большинстве случаев является лишь подпрограммой и применяется к разным кубитам большое число раз. В свою очередь, вычисляемые при помощи битовых операций индексы i0, i1 и iq зависят лишь от параметров количества кубитов n и номера кубита q. Число кубитов обычно фиксировано, соответственно, можно вычислить эти индексы заранее для всех q от 1 до n. Для хранения потребуется лишь массив целочисленных переменных линейного размера 3n в то время, как обрабатываемые данные имеют экспоненциальный размер. Очевидно, что такая оптимизация критически необходима при реализации алгоритма на вычислительных устройствах или языках программирования с отсутствием быстрых битовых операций (примером может служить среда Matlab).
2.2 Возможные способы и особенности параллельной реализации алгоритма
Основной способ параллельной реализации очевиден - необходимо распараллеливание основного цикла (параллельное вычисление различных компонент выходного вектора-состояния) и, желательно, операций умножения. На машинах с общей памятью такой вариант распараллеливания приводит к ускорению, близкому к максимально-возможному.
Однако, данный способ сталкивается с проблемами локальности данных. Анализируя математическая описание и информационные графы алгоритма легко видеть, что при использовании большого числа узлов с собственной памятью количество необходимых пересылок между узлами становится сопоставимым с количеством вычислений, что приводит к существенной потере эффективности. Возможны разные пути частичного решения этой проблемы, например, кэширование или использование парадигмы программирования SHMEM, однако, столь сильная нелокальность использования данных всё равно не позволяет добиться хорошей эффективности.
Алгоритм реализован (в основном последовательные версии) в различных библиотеках для квантовой информатики и квантового компьютерного моделирования. Например: QLib, libquantum, QuantumPlayground, LIQUiD.
2.3 Результаты прогонов
2.4 Выводы для классов архитектур
Исходя из высочайшей возможности параллелизации и при этом наличия существенной нелокальности обращения к данным, эффективная и хорошо масштабируемая параллельная реализация алгоритма однокубитного квантового преобразования легко достижима на машинах с общей памятью. Реализация же на машинах с разделяемой памятью имеет низкую эффективность и требует специальных подходов для уменьшения времени работы. Можно отметить, что данная задача является хорошим плацдармом для разработки методов решения задач с интенсивным использованием данных и низкой локальностью.
3 Литература
