Алгоритм Беллмана-Форда

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Алгоритм Беллмана-Форда предназначен для решения задачи поиска кратчайшего пути на графе. Для заданного ориентированного взвешенного графа алгоритм находит кратчайшие расстояния от выделенной вершины-источника до всех остальных вершин графа. Алгоритм Беллмана-Форда масштабируется хуже других алгоритмов решения указанной задачи (сложность [math]O(mn)[/math] против [math]O(m + n\ln n)[/math] у алгоритма Дейкстры), однако его отличительной особенностью является применимость к графам с произвольными, в том числе отрицательными, весами.

1.2 Математическое описание алгоритма

Пусть задан граф [math]G = (V, E)[/math] с весами рёбер [math]f(e)[/math] и выделенной вершиной-источником [math]u[/math]. Обозначим через [math]d(v)[/math] кратчайшее расстояние от источника [math]u[/math] до вершины [math]v[/math].

Алгоритм Беллмана-Форда ищет функцию [math]d(v)[/math] как единственное решение уравнения

[math] d(v) = \min \{ d(w) + f(e) \mid e = (w, v) \in E \}, \quad \forall v \ne u, [/math]

с начальным условием [math]d(u) = 0[/math].

1.3 Вычислительное ядро алгоритма

Основной операцией алгоритма является релаксация ребра: если [math]e = (w, v) \in E[/math] и [math]d(v) \gt d(w) + f(e)[/math], то производится присваивание [math]d(v) \leftarrow d(w) + f(e)[/math].

1.4 Макроструктура алгоритма

Алгоритм последовательно уточняет значения функции [math]d(v)[/math].

• В самом начале производится присваивание [math]d(u) = 0[/math], [math]d(v) = \infty[/math], [math]\forall v \ne u[/math].
• Далее происходит [math]n-1[/math] итерация, в ходе каждой из которых производится релаксация всех рёбер графа.

Структуру можно описать следующим образом:

1. Инициализация: всем вершинам присваивается предполагаемое расстояние [math]t(v)=\infty[/math], кроме вершины-источника, для которой [math]t(u)=0[/math] .

2. Релаксация множества рёбер [math]E[/math]

а) Для каждого ребра [math]e=(v,z) \in E[/math] вычисляется новое предполагаемое расстояние [math]t^' (z)=t(v)+ w(e)[/math].

б) Если [math]t^' (z)\lt t(z)[/math], то происходит присваивание [math]t(z) := t' (z)[/math] (релаксация ребра [math]e[/math] ).

3. Алгоритм производит релаксацию всех рёбер графа до тех пор, пока на очередной итерации происходит релаксация хотя бы одного ребра.

Если на [math]n[/math]-й итерации всё ещё производилась релаксацию рёбер, то в графе присутствует цикл отрицательной длины. Ребро [math]e=(v,z)[/math], лежащее на таком цикле, может быть найдено проверкой следующего условия (проверяется для всех рёбер за линейное время): [math]t(v)+w(e)\lt d(z)[/math]

1.5 Схема реализации последовательного алгоритма

Последовательный алгоритм реализуется следующим псевдокодом:

Входные данные:
  граф с вершинами V, рёбрами E с весами f(e);
  вершина-источник u.
Выходные данные: расстояния d(v) до каждой вершины v ∈ V от вершины u.

for each v ∈ V do d(v) := ∞
d(u) = 0

for i from 1 to |V| - 1:
    for each e = (w, v) ∈ E:
        if d(v) > d(w) + f(e):
            d(v) := d(w) + f(e)

1.6 Последовательная сложность алгоритма

Алгоритм выполняет [math]n-1[/math] итерацию, на каждой из которых происходит релаксация [math]m[/math] рёбер. Таким образом, общий объём работы составляет [math]O(mn)[/math] операций.

Константа в оценке сложности может быть уменьшена за счёт использования следующих двух стандартных приёмов.

1. Если на очередной итерации не произошло ни одной успешной релаксации, то алгоритм завершает работу.
2. На очередной итерации рассматриваются не все рёбра, а только выходящие из вершин, для которых на прошлой итерации была выполнена успешная релаксация (на первой итерации – только рёбра, выходящие из источника).

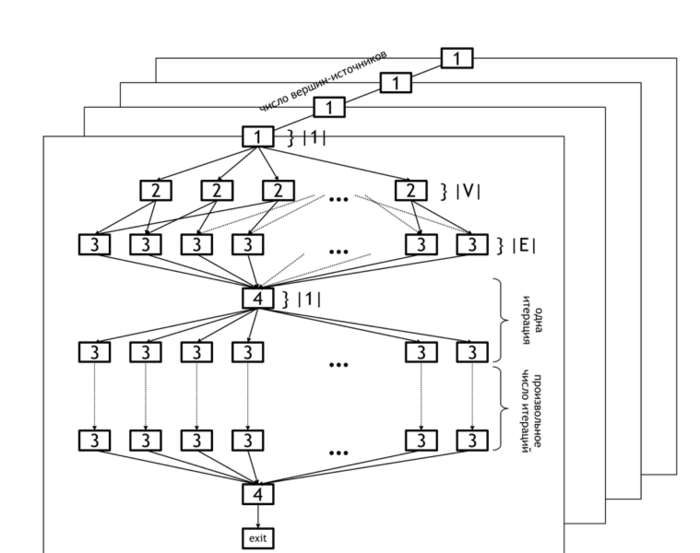
1.7 Информационный граф

На рисунке 1 представлен информационный граф алгоритма, демонстрирующий описанные уровни параллелизма. На приведенном далее информационном графе нижний уровень параллелизма обозначен в горизонтальных плоскостях. Множество всех плоскостей представляет собой верхний уровень параллелизма (операции в каждой плоскости могут выполняться параллельно).

Нижний уровень параллелизма на графе алгоритма расположен на уровнях {2 и 3}, соответствующим операциям инициализации массива дистанций (2) и обновления массива c использованием данных массива ребер {3}. Операция {4} - проверка того, были ли изменения на последней итерации и выход из цикла, если таковых не было.

Рисунок 1. Информационный граф обобщенного алгоритма Беллмана-Форда.

Верхний уровень параллелизма, как уже говорилось, заключается в параллельном подсчете дистанций для различных вершин-источников, и на рисунке отмечен разными плоскостями.

1.8 Ресурс параллелизма алгоритма

При использовании атомарных операций для вычисления минимума релаксация рёбер может производится параллельно. В этом случае потребуется [math]O(n)[/math] шагов при использовании [math]O(m)[/math] процессоров.

Алгоритм Δ-шагания может рассматриваться как параллельная версия алгоритма Беллмана-Форда.

1.9 Входные и выходные данные алгоритма

Входные данные: взвешенный граф [math](V, E, W)[/math] ([math]n[/math] вершин [math]v_i[/math] и [math]m[/math] рёбер [math]e_j = (v^{(1)}_{j}, v^{(2)}_{j})[/math] с весами [math]f_j[/math]), вершина-источник [math]u[/math].

Объём входных данных: [math]O(m + n)[/math].

Выходные данные (возможные варианты):

1. для каждой вершины [math]v[/math] исходного графа – последнее ребро [math]e^*_v = (w, v)[/math], лежащее на кратчайшем пути от вершины [math]u[/math] к [math]v[/math], или соответствующая вершина [math]w[/math];
2. для каждой вершины [math]v[/math] исходного графа – суммарный вес [math]f^*(v)[/math] кратчайшего пути от от вершины [math]u[/math] к [math]v[/math].

Объём выходных данных: [math]O(n)[/math].

1.10 Свойства алгоритма

Алгоритм может распознавать наличие отрицательных циклов в графе. Ребро [math]e = (v, w)[/math] лежит на таком цикле, если вычисленные алгоритмом кратчайшие расстояния [math]d(v)[/math] удовлетворяют условию

[math] d(v) + f(e) \lt d(w), [/math]

где [math]f(e)[/math] – вес ребра [math]e[/math]. Условие может быть проверено для всех рёбер графа за время [math]O(m)[/math].

2 Программная реализация алгоритма

2.2 Локальность данных и вычислений

2.2.1 Локальность реализации алгоритма

2.2.1.1 Структура обращений в память и качественная оценка локальности

В ходе исполнения алгоритма данные о рёбрах читаются последовательно (идеальная локальность), однако чтение и обновление вектора расстояний зависит от структуры графа и обычно является случайным (локальность отсутствует).

2.2.1.2 Количественная оценка локальности

Для обработки одного ребра:

1. чтение данных о ребре не должно вызывать промаха по кэшу, так как данные о рёбрах читаются последовательно
2. чтение и обновление массива расстояний, напротив, почти наверняка вызовет два промаха по кэшу (по одному для каждого конца ребра)

2.3 Возможные способы и особенности параллельной реализации алгоритма

Программа, реализующая алгоритм поиска кратчайших путей, состоит из двух частей: части, отвечающей за общую координацию вычислений, а так же параллельные вычисления на многоядерных CPU, и GPU части, отвечающей только за вычисления на графическом ускорителе.

2.4 Масштабируемость алгоритма и его реализации

2.4.1 Масштабируемость алгоритма

Алгоритм обладает значительным потенциалом масштабируемости, так как каждое ребро обрабатывается независимо и можно поручить каждому вычислительному процессу свою часть рёбер графа. Узким местом является доступ к разделяемому всеми процессами массиву расстояний. Алгоритм позволяет ослабить требования к синхронизации данных этого массива между процессами (когда один процесс может не сразу увидеть новое значение расстояния, записанное другим процессом), за счёт, может быть, большего количества глобальных итераций.

2.4.2 Масштабируемость реализации алгоритма

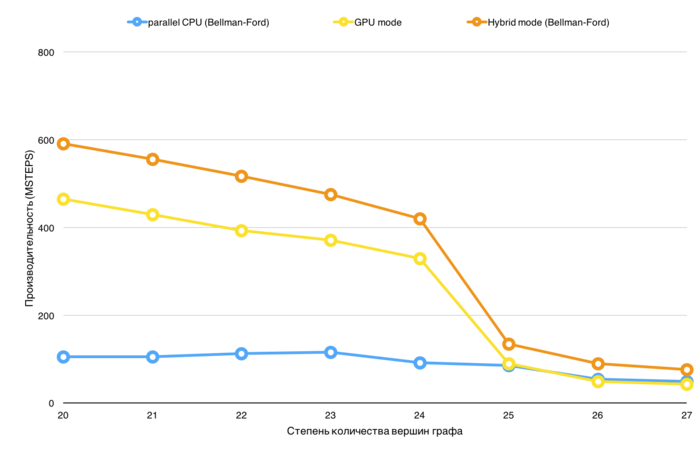
Проведём исследование масштабируемости параллельной реализации алгоритма Беллмана-Форда согласно методике. Исследование проводилось на суперкомпьютере "Ломоносов-2 Суперкомпьютерного комплекса Московского университета.

Набор и границы значений изменяемых параметров запуска реализации алгоритма:

• число процессоров [1 : 28] с шагом 1;
• размер графа [2^20 : 2^27].

Проведем отдельные исследования сильной масштабируемости вширь реализации алгоритма Беллмана-Форда.

Производительность определена как TEPS (от англ. Traversed Edges Per Second), то есть число ребер графа, который алгоритм обрабатывает в секунду. С помощью данной метрики можно сравнивать производительность для различных размеров графа, оценивая, насколько понижается эффективность обработки графа при увеличении его размера.

Рисунок 2. Параллельная реализация алгоритма Беллмана-Форда масштабируемость различных версий реализации алгоритма: производительность в зависимости от размера графа

2.7 Существующие реализации алгоритма

• C++: Boost Graph Library (функция bellman_ford_shortest).
• Python: NetworkX (функция bellman_ford).
• Java: JGraphT (класс BellmanFordShortestPath).