Итерация алгоритма dqds: различия между версиями
| [непроверенная версия] | [непроверенная версия] |
| Строка 16: | Строка 16: | ||
'''Итерация алгоритма dqds''' является одним шагом [[Алгоритм dqds нахождения сингулярных чисел двухдиагональной матрицы|итерационного алгоритма для нахождения сингулярных чисел | '''Итерация алгоритма dqds''' является одним шагом [[Алгоритм dqds нахождения сингулярных чисел двухдиагональной матрицы|итерационного алгоритма для нахождения сингулярных чисел | ||
| − | |||
двухдиагональной матрицы]]. Основные вычисления алгоритма dqds приходятся именно на внутреннюю итерацию. Внешняя часть алгоритма отвечает за контроль сходимости и выбор сдвигов <math>\delta,</math> что основано на довольно сложной теории и имеет различные реализации, но в то же время не влияет на вычислительные аспекты. В связи с этим dqds-итерация и [[Алгоритм dqds нахождения сингулярных чисел двухдиагональной матрицы|dqds-алгоритм]] рассматриваются отдельно. | двухдиагональной матрицы]]. Основные вычисления алгоритма dqds приходятся именно на внутреннюю итерацию. Внешняя часть алгоритма отвечает за контроль сходимости и выбор сдвигов <math>\delta,</math> что основано на довольно сложной теории и имеет различные реализации, но в то же время не влияет на вычислительные аспекты. В связи с этим dqds-итерация и [[Алгоритм dqds нахождения сингулярных чисел двухдиагональной матрицы|dqds-алгоритм]] рассматриваются отдельно. | ||
| Строка 85: | Строка 84: | ||
=== Информационный граф === | === Информационный граф === | ||
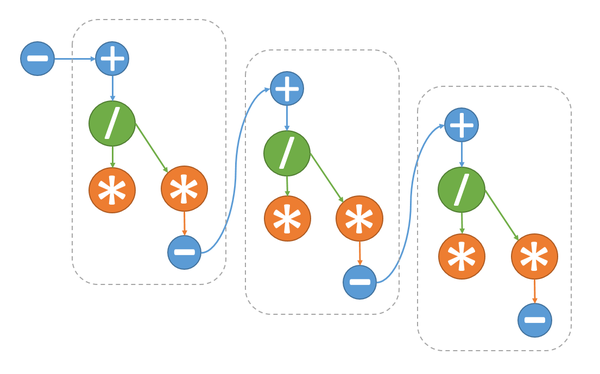
| − | [[file:dqds.png|thumb|center|600px|Рисунок 1. Граф алгоритма без отображения входных и выходных данных.]] | + | [[file:dqds.png|thumb|center|600px|Рисунок 1. Граф алгоритма для n=4 без отображения входных и выходных данных.]] |
=== Ресурс параллелизма алгоритма === | === Ресурс параллелизма алгоритма === | ||
| − | Как видно из информационного графа алгоритма, на каждом шаге основного цикла возможно лишь параллельное выполнение | + | Как видно из информационного графа алгоритма, на каждом шаге основного цикла возможно лишь параллельное выполнение операции умножения (2.2) и умножения+сложения (2.4). Это позволяет сократить число ярусов на одной итерации цикла c 5 до 4, а общее число ярусов алгоритма с 5n-4 до 4n-3. Ярусы с операциями умножения состоят из двух операций, остальные же из одной. |
| + | |||
| + | === Входные и выходные данные алгоритма === | ||
| + | |||
| + | '''Входные данные''': Квадраты элементов основной и верхней побочной диагонали двухдиагональной матрицы (вектора <math>q</math> длины n и <math>e</math> длины n-1), а также параметр сдвига <math>\delta</math>. | ||
| + | |||
| + | '''Объём входных данных''': <math>2n</math>. | ||
| + | |||
| + | '''Выходные данные''': Квадраты элементов основной и верхней побочной диагонали выходной двухдиагональной матрицы. | ||
| + | |||
| + | '''Объём выходных данных''': <math>2n-1</math>. | ||
| + | |||
| + | === Свойства алгоритма=== | ||
| + | |||
| + | Соотношение последовательной и параллельной сложности при наличии возможности параллельного выполнения операций умножения составляет <math>\frac{5n-4}{4n-3}</math>, т.е. алгоритм плохо распараллеливается. | ||
| + | |||
| + | Вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных - константа. | ||
| + | |||
| + | Описываемый алгоритм является полностью детерминированным. | ||
| + | |||
| + | |||
| + | == Программная реализация алгоритмов == | ||
| + | === Особенности реализации последовательного алгоритма === | ||
| + | |||
| + | Алгоритм на языке Matlab может быть записать так: | ||
| + | <source lang="matlab"> | ||
| + | |||
| + | d = q(1)-delta; | ||
| + | for j = 1:n-1 | ||
| + | q(j)=d+e(j); | ||
| + | t=q(j+1)/q(j); | ||
| + | e(j) = e(j)*t; | ||
| + | d = d*t-delta; | ||
| + | end | ||
| + | q(n) = d; | ||
| + | |||
| + | </source> | ||
| + | |||
| + | |||
| + | === Локальность данных и вычислений === | ||
| + | |||
| + | Легко видеть, что локальность данных высока. Её легко повысить, размещая рядом соответствующие элементы массивов e и q, однако, это не оказывает существенного влияния на производительность в силу константного количества операций относительно объема обрабатываемых данных. | ||
| + | |||
| + | === Возможные способы и особенности параллельной реализации алгоритма === | ||
| + | |||
| + | Итерация dqds практически полностью последовательна. Единственная возможность - одновременное выполнение операции умножения (2.3) и опрерации (2.4) умножения и сложения, что дает небольшой выигрыш в производительности. | ||
| + | |||
| + | === Масштабируемость алгоритма и его реализации === | ||
| + | |||
| + | Алгоритм не является масштабируемым, максимального эффекта ускорения можно добиться на двух независимых процессорах. | ||
| + | |||
| + | |||
| + | === Выводы для классов архитектур === | ||
| + | |||
| + | Эффективное выполнение алгоритма возможно только на вычислительных устройствах с одним или двумя ядрами. | ||
| + | |||
| + | === Существующие реализации алгоритма === | ||
| + | Перечень реализаций приведен на странице [[Алгоритм dqds нахождения сингулярных чисел двухдиагональной матрицы|алгоритма dqds]]. | ||
| + | |||
| + | == Литература == | ||
| + | |||
| + | <references /> | ||
Версия 16:40, 23 августа 2015
| Алгоритм dqds нахождения сингулярных чисел двухдиагональной матрицы | |
| Последовательный алгоритм | |
| Последовательная сложность | [math]5n-4[/math] |
| Объём входных данных | [math]2n[/math] |
| Объём выходных данных | [math]2n[/math] |
| Параллельный алгоритм | |
| Высота ярусно-параллельной формы | [math]4n-3[/math] |
| Ширина ярусно-параллельной формы | [math]2[/math] |
Основные авторы описания: А.Ю.Чернявский
Содержание
- 1 Свойства и структура алгоритмов
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритмов
- 3 Литература
1 Свойства и структура алгоритмов
1.1 Общее описание алгоритма
Итерация алгоритма dqds является одним шагом итерационного алгоритма для нахождения сингулярных чисел двухдиагональной матрицы. Основные вычисления алгоритма dqds приходятся именно на внутреннюю итерацию. Внешняя часть алгоритма отвечает за контроль сходимости и выбор сдвигов [math]\delta,[/math] что основано на довольно сложной теории и имеет различные реализации, но в то же время не влияет на вычислительные аспекты. В связи с этим dqds-итерация и dqds-алгоритм рассматриваются отдельно.
1.2 Математическое описание алгоритма
Формулы алгоритма следующие:
- [math] \widehat{q}_j = q_j + e_j - \widehat{e}_{j-1} - \delta, \quad j \in [1,n-1]\\ \widehat{e}_j = e_j \cdot q_{j+1} / \widehat{q}_j, \quad j \in [1,n-1]\\ \widehat{q}_n = q_n - \widehat{e}_{n-1} - \delta. [/math]
Здесь [math]q_j, \; j \in [1,n][/math] и [math]e_j, \; j \in [1,n-1][/math] - квадраты элемнтов главной и верхней побочной диагональ соответственно. Крышка означает выходные переменные, а
[math]\delta[/math] - сдвиг (параметр алгоритма). Такая математическая запись наиболее компактна и соответсвует так называемой qds-итерации.
Представим также математическую запись, приближенную к dqds-итерации (с математической точки зрения qds и dqds-итерации эквивалентны) с введенными вспомогательными переменными
[math]t_j[/math] и [math]d_j:[/math]
- [math] d_1 = q_1 - \delta, \; q_n = d_n \\ для \; j\in [1,n-1]: \\ \widehat{q}_j = d_j + e_j\\ t_j = q_{j+1}/\widehat{q}_j\\ \widehat{e}_j=e_j \cdot t_j \\ d_{j+1} = d \cdot t - \delta \\ [/math]
Отметим, что при [math]\delta=0[/math] две итерации dqds эквиваленты одной QR-итерации.
1.3 Вычислительное ядро алгоритма
Вычислительным ядром алгоритма является производимое n-1 раз вычисление, содержащие по одной операции сложения, вычитания и деления, а также две операции умножения.
1.4 Макроструктура алгоритма
Алгоритм состоит из отдельного вычисления начального значения вспомогательной переменной [math]d[/math] и последующим (n-1)-кратным выполнением повторяющейся последовательности из 5 операций (+,/,*,*,-).
1.5 Схема реализации последовательного алгоритма
Отметим, что выходные данные сразу могут быть записаны на место входных (это учтено в схеме), также для хранения вспомогательных переменных [math]t_j[/math] и [math]d_j[/math] достаточно двух перезаписываемых переменных.
1. Вычисляется начальное значение вспомогательной переменной [math]d = q_1-\delta.[/math]
2. Производится цикл по j от 1 до n-1, состоящий из:
- 2.1 Вычисляется значение [math]q_j = d + e_j;[/math]
- 2.2 Вычисляется значение вспомогательной переменной [math]t = q_{j+1}/q_j;[/math]
- 2.3 Вычисляется значение [math]e_j = e_j \cdot t;[/math]
- 2.4 Вычисляется значение вспомогательной переменной [math]d = d \cdot t - \delta.[/math]
3. Вычисляется [math]q_n = d.[/math]
1.6 Последовательная сложность алгоритма
Для выполнения одной итерации dqds необходимо выполнить:
- [math]n-1[/math] делений,
- [math]2n-2[/math] умножений,
- [math]2n-1[/math] сложений/вычитаний.
Таким образом одна dqds-итерация имеет линейную сложность.
1.7 Информационный граф
1.8 Ресурс параллелизма алгоритма
Как видно из информационного графа алгоритма, на каждом шаге основного цикла возможно лишь параллельное выполнение операции умножения (2.2) и умножения+сложения (2.4). Это позволяет сократить число ярусов на одной итерации цикла c 5 до 4, а общее число ярусов алгоритма с 5n-4 до 4n-3. Ярусы с операциями умножения состоят из двух операций, остальные же из одной.
1.9 Входные и выходные данные алгоритма
Входные данные: Квадраты элементов основной и верхней побочной диагонали двухдиагональной матрицы (вектора [math]q[/math] длины n и [math]e[/math] длины n-1), а также параметр сдвига [math]\delta[/math].
Объём входных данных: [math]2n[/math].
Выходные данные: Квадраты элементов основной и верхней побочной диагонали выходной двухдиагональной матрицы.
Объём выходных данных: [math]2n-1[/math].
1.10 Свойства алгоритма
Соотношение последовательной и параллельной сложности при наличии возможности параллельного выполнения операций умножения составляет [math]\frac{5n-4}{4n-3}[/math], т.е. алгоритм плохо распараллеливается.
Вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных - константа.
Описываемый алгоритм является полностью детерминированным.
2 Программная реализация алгоритмов
2.1 Особенности реализации последовательного алгоритма
Алгоритм на языке Matlab может быть записать так:
d = q(1)-delta;
for j = 1:n-1
q(j)=d+e(j);
t=q(j+1)/q(j);
e(j) = e(j)*t;
d = d*t-delta;
end
q(n) = d;
2.2 Локальность данных и вычислений
Легко видеть, что локальность данных высока. Её легко повысить, размещая рядом соответствующие элементы массивов e и q, однако, это не оказывает существенного влияния на производительность в силу константного количества операций относительно объема обрабатываемых данных.
2.3 Возможные способы и особенности параллельной реализации алгоритма
Итерация dqds практически полностью последовательна. Единственная возможность - одновременное выполнение операции умножения (2.3) и опрерации (2.4) умножения и сложения, что дает небольшой выигрыш в производительности.
2.4 Масштабируемость алгоритма и его реализации
Алгоритм не является масштабируемым, максимального эффекта ускорения можно добиться на двух независимых процессорах.
2.5 Выводы для классов архитектур
Эффективное выполнение алгоритма возможно только на вычислительных устройствах с одним или двумя ядрами.
2.6 Существующие реализации алгоритма
Перечень реализаций приведен на странице алгоритма dqds.