Участник:Kosean97/Метод встречи посередине в решении задачи дискретного логарифмирования в группе точек эллиптической кривой: различия между версиями
Kosean97 (обсуждение | вклад) |
Kosean97 (обсуждение | вклад) |
||
| Строка 106: | Строка 106: | ||
Будем считать генерацию точки за элементарную операцию. | Будем считать генерацию точки за элементарную операцию. | ||
Сложность этапа генерации базы точек есть <math>\sqrt{r}</math>, так как точки хранятся в связном списке, добавление составляет константную сложность. | Сложность этапа генерации базы точек есть <math>\sqrt{r}</math>, так как точки хранятся в связном списке, добавление составляет константную сложность. | ||
| − | Сортировка производится алгоритмом Q-Sort, тем самым будет выполнено порядка <math>\sqrt{r}\log r</math> операций. Поиск по созданной базе точек осуществляется алгоритмом бинарного поиска, таким образом, проверка на вхождение нужного элемента производится за <math>\log r</math> операций. | + | Сортировка производится алгоритмом Q-Sort, тем самым будет выполнено порядка <math>\sqrt{r}\log r</math> операций. Поиск по созданной базе точек осуществляется алгоритмом бинарного поиска, таким образом, проверка на вхождение нужного элемента производится за <math>\log r</math> операций. Вычисление логарифма по найденной паре выполняется за |
| + | константу. | ||
<br><br> | <br><br> | ||
Таким образом: | Таким образом: | ||
Версия 18:30, 3 декабря 2017
Алгоритм: Применение метода встречи посередине в решении задачи дискретного логарифмирования в группе точек эллиптической кривой
Автор описания: Конюхов Сергей
Эллиптическая криптография — раздел криптографии, который изучает асимметричные криптосистемы, основанные на эллиптических кривых над конечными полями. Основное преимущество эллиптической криптографии заключается в том, что на сегодняшний день не известно существование субэкспоненциальных алгоритмов[1] решения задачи дискретного логарифмирования. Использование эллиптических кривых для создания криптосистем было независимо предложено Нилом Коблицем и Виктором Миллером в 1985 году.
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
Задача дискретного логарифмирования[2] в общем виде заключается в поиске решения g^x=a в некоторой конечной абелевой группе G.
Мы же рассмотрим группу точек эллиптической кривой над полем {\mathbb Z}_p характеристики p \gt 3:
E( {\mathbb Z}_p ) = {\mathcal O} \cup \{ (x, y) \in {\mathbb Z}_p^2 \enspace|\enspace y^2 \equiv x^3 + Ax + B \enspace (mod \thinspace p) \}, где A, B \in {\mathbb Z}_p - константы, удовлетворяющие условию 4A^3+27B^2 \ne 0 \enspace (mod \thinspace p).
В качестве группы G возьмём циклическую подгруппу группы E( {\mathbb Z}_p ) порождённую элементом Q, то есть G=\langle Q \rangle.
Стоит отметить, что группа G является аддитивной, и задачу DLOG стоит переформулировать: в уравнении nQ=P требуется найти n.
1.1 Общее описание алгоритма
Метод "встречи посередине"[3] является вероятностным и основан на так называемом парадоксе дней рождений - для того, чтобы при выборке с возвратом из множества мощности r получить совпадение двух элементов с достаточно большой вероятностью, требуется произвести \sqrt{r} попыток.
Eсли мы найдем совпадение точек вида: lQ = kP, то мы можем получить решение задачи как n=lk^{-1}\enspace (mod \thinspace r).
1.2 Математическое описание алгоритма
G = \langle Q \rangle, |G| = r - циклическая подгруппа группы точек эллиптической кривой. Уравнение nQ = P.
Дано: E, Q, P, r - эллиптическая кривая, образующая группы G, логарифмируемый элемент, порядок группы.
Найти: n - искомый логарифм.
Алгоритм:
- Случайно выбрать \sqrt{r} чисел l_i \in {\mathbb Z}_r и сохранить точки вида l_iQ.
- Отсортировать полученные на предыдущем этапе точки по координате x.
- Для случайных k_j \in {\mathbb Z}_r вычислить точки k_jP и осуществить поиск на совпадение в сохранённом массиве.
- В случае успеха вычислить n=l_ik_j^{-1}\enspace (mod \thinspace r). В случае провала перейти к пункту 3.
1.3 Вычислительное ядро алгоритма
В описываемом алгоритме присутствует три вычислительных ядра: генерация базы данных, сортировка базы данных для дальнейшего поиска, генерация случайных точек - степеней изучаемой точки и поиск совпадений в созданной базе данных.
- Генерация базы данных.
Выбирается некоторый "квант" - число точек - степеней образующей, которые будут генерироваться за одну итерацию. До тех пор пока не наберётся достаточное количество точек, генерируем "квант" случайных точек. Генерация точек осуществляется следующим образом: выбирается псевдослучайное число, после чего образующая умножается на него. - Сортировка базы данных.
Полученная база точек - степеней образующей сортируется по икс-координате (точка А больше точки Б, если икс-координата точки А больше икс-координаты точки Б). Алгоритм сортировки, например, быстрая сортировка. - Генерация и поиск.
Генерируется "квант" точек - степеней изучаемой точки. После чего производится поиск в базе данных точки, обладающую той же икс-координатой, что и выбранная. Поиск осуществляется, например, бинарным поиском.
1.4 Макроструктура алгоритма
1.5 Схема реализации последовательного алгоритма
В качестве описания схемы реализации последовательного алгоритма можно привести данный фрагмент программы на языке С++.
int main( int argc, char** argv )
{
// Определяем группу, исследуемый элемент,
// а так же объем базы данных точек и количество точек,
// генерируемых за один раз, цель исследования.
DLogConfig config( "config.txt" );
DLogSolver solver( &argc, &argv, config );
do
{
// Сгенерировать некоторое количество точек - степеней образующей.
solver.GenerateDatabase();
}
// До тех пор, пока нужное количество точек не будет создано.
while( !solver.DatabaseFull() );
// Сортировка полученной базы данных.
solver.PrepareDatabase();
do
{
// Сгенерировать некоторое количество точек - степеней исследуемого элемента.
solver.GeneratePoints();
// Поиск совпадений в базе данных.
solver.LookThrowDatabase();
}
// Повторять до тех пор, пока совпадение не будет найдено.
while( !solver.SolutionFound() );
// Вывести ответ.
solver.PrintAnswer();
return EXIT_SUCCESS;
}
1.6 Последовательная сложность алгоритма
Будем считать генерацию точки за элементарную операцию.
Сложность этапа генерации базы точек есть \sqrt{r}, так как точки хранятся в связном списке, добавление составляет константную сложность.
Сортировка производится алгоритмом Q-Sort, тем самым будет выполнено порядка \sqrt{r}\log r операций. Поиск по созданной базе точек осуществляется алгоритмом бинарного поиска, таким образом, проверка на вхождение нужного элемента производится за \log r операций. Вычисление логарифма по найденной паре выполняется за
константу.
Таким образом:
- временная сложность алгоритма есть \sqrt{r}\log r,
- оценка используемой памяти есть \sqrt{r},
где r - это порядок группы G точек эллиптической кривой.
1.7 Информационный граф
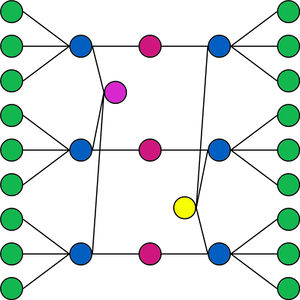
На рисунке 1 можно видеть информационный граф алгоритма дискретного логарифмирования методом встречи посередине. Так, зеленым вершинам соответствует операция случайного выбора точки из группы. Каждая точка сохраняется в один из связных списков, группировка происходит на основании икс-координаты точки. Вершине, отмеченной розовым цветом, соответствует подсчёт общего количества точек. После этого, каждая группа точек по отдельности сортируется. Данному процессу соответствуют вершины, обозначенные красным цветом. Следующим этапом мы генерируем еще одно множество точек, и раздельно, в соответствии с икс-координатой, их сохраняем. Аналогично, этим операциям соответствуют зеленые и синие вершины (справа). В каждой группе из выбранных точек ищется вхождение соответствующего элемента в отсортированном массиве. Желтой вершине соответствует операция, результатом которой есть ответ на вопрос, была ли найдена коллизия.
1.8 Ресурс параллелизма алгоритма
1.9 Входные и выходные данные алгоритма
1.10 Свойства алгоритма
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
3 Литература
- ↑ Василенко О.Н. Теоретико-числовые алгоритмы в криптографии. Изд. 2-е. доп. - М.: МЦНМО, 2006. - 336 с.
- ↑ Применко Э.А. Алгебраические основы криптографии: Учебное пособие. Изд. 2-е, испр. - М.: ЛЕНАНД, 2015. - 288 с.
- ↑ Бабенко Л.К., Ищукова Е.А., Сидоров И.Д. Параллельные алгоритмы для решения задач защиты информации. - М.: Горячая линия - Телеком, 2014. - 304 с.