Участник:Sergey.protserov/Метод Якоби решения СЛАУ: различия между версиями
(+= 2.4, 2.7) |
(+= 1.7) |
||
| Строка 77: | Строка 77: | ||
=== Последовательная сложность алгоритма === | === Последовательная сложность алгоритма === | ||
Шаг 2 предыдущего пункта требует выполнения <math>m</math> операций деления вещественных чисел, шаг 3 (с учётом того, что матрица <math>D^{-1}</math> — диагональная) требует выполнения <math>m^{2}</math> операций умножения вещественных чисел, аналогично шаг 4 требует <math>m</math> операций умножения, а каждая итерация шага 5 требует <math>m^{2}</math> умножений и <math>m^{2} + 2m</math> сложений/вычитаний. | Шаг 2 предыдущего пункта требует выполнения <math>m</math> операций деления вещественных чисел, шаг 3 (с учётом того, что матрица <math>D^{-1}</math> — диагональная) требует выполнения <math>m^{2}</math> операций умножения вещественных чисел, аналогично шаг 4 требует <math>m</math> операций умножения, а каждая итерация шага 5 требует <math>m^{2}</math> умножений и <math>m^{2} + 2m</math> сложений/вычитаний. | ||
| + | |||
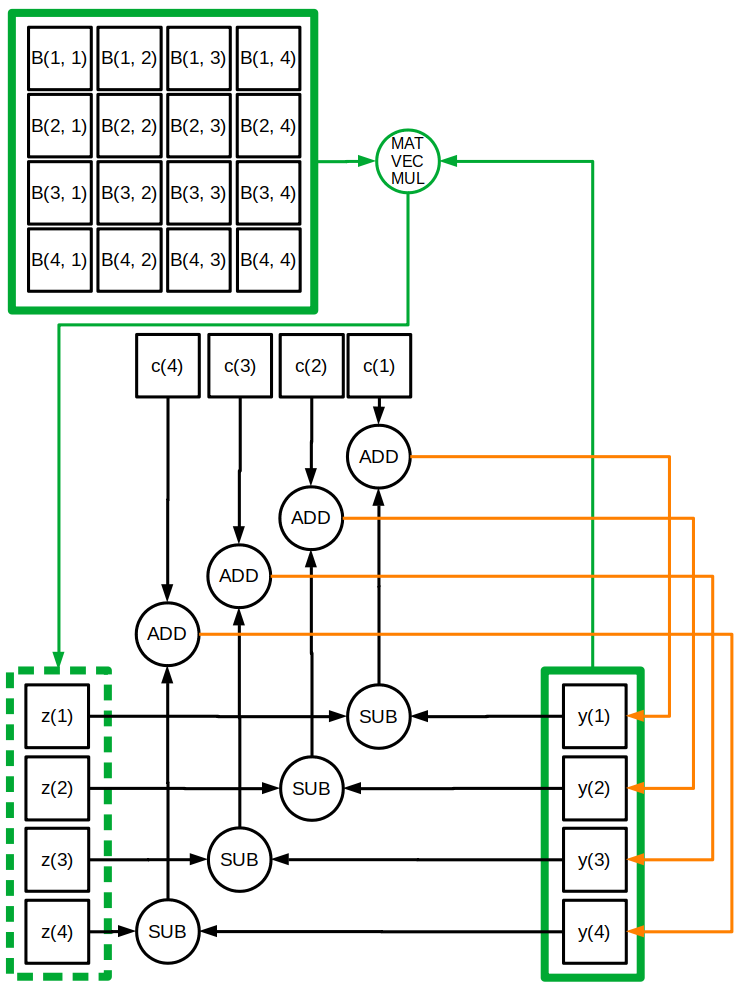
| + | === Информационный граф === | ||
| + | Граф пятого шага алгоритма: | ||
| + | [[File:S_P_Jacobi_Algo_graph.png]] | ||
| + | |||
| + | '''MM''' обозначает матричное умножение (конкретно — умножение матрицы на вектор), '''SUB''' — вычитание векторов, '''ADD''' — сложение векторов. | ||
=== Ресурс параллелизма алгоритма === | === Ресурс параллелизма алгоритма === | ||
| Строка 145: | Строка 151: | ||
Из приведённых данных видна хорошая слабая масштабируемость алгоритма, а так же тот факт, что увеличение числа процессов с 32 до 64 при входной матрице порядка 2500 уже не даёт значительного выигрыша во времени работы, т.е., что сильная масштабируемость с некоторого момента начинает падать. В исследуемой реализации не осуществляется распараллеливание шагов 2 и 4 алгоритма, т.к. ожидалось, что распределение выполнения <math>2m</math> операций по процессам не принесёт значительного выигрыша из-за издержек на пересылки множества малых порций данных, а эксперимент показал, что во всех рассмотренных случаях временные затраты на выполнение шагов 2 и 4 в совокупности не превышают <math>4 \cdot 10^{-4}</math> секунд. | Из приведённых данных видна хорошая слабая масштабируемость алгоритма, а так же тот факт, что увеличение числа процессов с 32 до 64 при входной матрице порядка 2500 уже не даёт значительного выигрыша во времени работы, т.е., что сильная масштабируемость с некоторого момента начинает падать. В исследуемой реализации не осуществляется распараллеливание шагов 2 и 4 алгоритма, т.к. ожидалось, что распределение выполнения <math>2m</math> операций по процессам не принесёт значительного выигрыша из-за издержек на пересылки множества малых порций данных, а эксперимент показал, что во всех рассмотренных случаях временные затраты на выполнение шагов 2 и 4 в совокупности не превышают <math>4 \cdot 10^{-4}</math> секунд. | ||
| + | |||
=== Существующие реализации алгоритма === | === Существующие реализации алгоритма === | ||
Авторам статьи не известно о существовании хороших реализаций данного алгоритма. | Авторам статьи не известно о существовании хороших реализаций данного алгоритма. | ||
| + | |||
== Литература == | == Литература == | ||
<references /> | <references /> | ||
Версия 20:26, 28 ноября 2019
Содержание
- 1 Свойства и структура алгоритмов
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 2 Программная реализация алгоритма
- 3 Литература
1 Свойства и структура алгоритмов
1.1 Общее описание алгоритма
Метод Якоби -- одношаговый стационарный итерационный метод решения СЛАУ вида [math]Ay = f[/math], где [math] A = \left( \begin{array}{ccc} a_{11} & \dots & a_{1m} \\ \vdots & \ddots & \vdots \\ a_{m1} & \dots & a_{mm} \\ \end{array} \right) [/math], [math] f = \left( \begin{array}{c} f_{1} \\ \vdots \\ f_{m} \\ \end{array} \right) [/math], [math] y = \left( \begin{array}{c} y_{1} \\ \vdots \\ y_{m} \\ \end{array} \right) [/math], [math]\det A \ne 0[/math].
Каноническая форма одношагового стационарного итерационного метода имеет вид [1]: [math] B\frac{y^{n+1} - y^{n}}{\tau} + Ay^{n} = f, \quad n = 0,\,1,\,\dots\,, [/math]
где [math]B[/math] — невырожденная матрица [math]m \times m[/math], [math]\tau \in \mathbb{R}[/math], [math]y^{0}[/math] — заданное начальное приближение. Решение исходной СЛАУ находится приближённо посредством последовательных итераций. На [math]n[/math]-ом шаге находится [math]y^{n+1}[/math] — очередное приближение для искомого решения [math]y[/math].
В методе Якоби [math]\tau = 1[/math], [math]B = D[/math], где [math]D[/math] — диагональная матрица, элементы которой совпадают с элементами, стоящими на главной диагонали матрицы [math]A[/math].
Достаточным условием сходимости метода является свойство строгого диагонального преобладания у матрицы [math]A[/math]. [2]
1.2 Математическое описание алгоритма
В обозначениях предыдущего пункта выражение для [math]y^{n+1}[/math] через [math]y^{n}[/math]: [math]y^{n+1} = D^{-1}\left(D-A\right)y^{n} + D^{-1}f[/math].
В поэлементной записи:
[math]y^{n+1}_{i} = \frac{1}{a_{ii}}\left(f_{i} - \sum_{j=1,\,j \ne i}^{m}a_{ij}y^{n}_{j}\right),\quad i = 1,\,\dots,\,m[/math].
В качестве условия окончания итерационного процесса можно использовать условие [math]\left\lVert y^{n+1} - y^{n}\right\rVert \le \varepsilon[/math], где [math]\varepsilon[/math] — заданная точность. Кроме того, можно ограничить максимальное число итераций, задав [math]n_{max}[/math]. Для оценки ошибки можно использовать невязку [math]Ay^{n+1} - f[/math].
1.3 Вычислительное ядро алгоритма
Основное время работы алгоритма приходится на последовательные вычисления векторов [math]y^{n+1}[/math] по формуле, приведённой в предыдущем пункте, при уже вычисленных в начале работы алгоритма матрице [math]D^{-1}A[/math] и векторе [math]D^{-1}f[/math].
1.4 Макроструктура алгоритма
В описываемом алгоритме можно выделить следующие макрооперации:
- вычисление [math]D^{-1}[/math]
- вычисление [math]D^{-1}A[/math]
- вычисление [math]D^{-1}f[/math]
- вычисление [math]y^{n+1} = \left(I - D^{-1}A\right)y^{n} + D^{-1}f[/math]
Макрооперации 1-3 выполняются единожды, и в силу того, что матрица [math]D[/math] — диагональная, занимают лишь незначительную часть времени работы алгоритма.
Макрооперация 4 выполняется многократно до наступления сходимости или достижения максимального числа итераций, поэтому она составляет вычислительное ядро алгоритма.
Кроме того, если в качестве критерия завершения работы алгоритма используется условие [math]\left\lVert y^{n+1} - y^{n}\right\rVert \le \varepsilon[/math], требуется также вычислять указанную величину. В дальнейшем при описании алгоритма мы будем предполагать, что этот критерий не используется, а используется завершение работы по достижении максимального числа итераций.
1.5 Схема реализации последовательного алгоритма
- составить диагональную матрицу [math]D[/math]
- вычислить [math]D^{-1}[/math]
- вычислить [math]D^{-1}A[/math]
- вычислить [math]D^{-1}f[/math]
- выполнять вычисления по формуле [math]y^{n+1} = \left(I - D^{-1}A\right)y^{n} + D^{-1}f[/math], [math]n = 0,\,1,\,\dots,\,n_{max}[/math]
При этом на [math]n[/math]-ом шаге итераций необходимо хранить оба вектора [math]y^{n}[/math], [math]y^{n+1}[/math].
1.6 Последовательная сложность алгоритма
Шаг 2 предыдущего пункта требует выполнения [math]m[/math] операций деления вещественных чисел, шаг 3 (с учётом того, что матрица [math]D^{-1}[/math] — диагональная) требует выполнения [math]m^{2}[/math] операций умножения вещественных чисел, аналогично шаг 4 требует [math]m[/math] операций умножения, а каждая итерация шага 5 требует [math]m^{2}[/math] умножений и [math]m^{2} + 2m[/math] сложений/вычитаний.
1.7 Информационный граф
MM обозначает матричное умножение (конкретно — умножение матрицы на вектор), SUB — вычитание векторов, ADD — сложение векторов.
1.8 Ресурс параллелизма алгоритма
Шаг 2 требует один ярус из [math]m[/math] операций деления, шаг 3 требует один ярус из [math]m^{2}[/math] операций умножения, шаг 4 требует один ярус из [math]m[/math] операций умножения, а каждая итерация шага 5 требует по [math]m[/math] ярусов умножений и сложений (в каждом из ярусов — [math]m[/math] операций) для выполнения умножения матрицы на вектор [3] и ещё два яруса по [math]m[/math] сложений/вычитаний, причём итерации выполняются последовательно.
1.9 Входные и выходные данные алгоритма
Входные данные:
- Вещественная [math]m \times m[/math] матрица [math]A[/math], вообще говоря, плотная
- Вещественный [math]m[/math]-мерный вектор правой части [math]f[/math]
- Вещественный [math]m[/math]-мерный вектор начального приближения [math]y^{0}[/math]
- Максимальное число итераций алгоритма [math]n_{max}[/math]
Выходные данные:
- Вещественный [math]m[/math]-мерный вектор приближённого решения [math]y^{n_{max}}[/math]
2 Программная реализация алгоритма
2.1 Масштабируемость алгоритма и его реализации
Зависимость времени работы алгоритма (100 итераций) в секундах от порядка входной матрицы и количества MPI-процессов:
| Кол-во процессов | |||||||
|---|---|---|---|---|---|---|---|
| Порядок матрицы | 1 | 2 | 4 | 8 | 16 | 32 | 64 |
| 2500 | 4.063 с | 2.072 с | 1.044 с | 0.533 с | 0.283 с | 0.186 с | 0.150 с |
| 5000 | 16.205 с | 8.283 с | 4.124 с | 2.059 с | 1.084 с | 0.600 с | 0.381 с |
| 10000 | 64.708 с | 33.071 с | 16.331 с | 8.145 с | 4.094 с | 2.208 с | 1.192 с |
| 20000 | 295.386 с | 132.868 с | 66.455 с | 33.137 с | 16.553 с | 8.329 с | 4.524 с |
Из приведённых данных видна хорошая слабая масштабируемость алгоритма, а так же тот факт, что увеличение числа процессов с 32 до 64 при входной матрице порядка 2500 уже не даёт значительного выигрыша во времени работы, т.е., что сильная масштабируемость с некоторого момента начинает падать. В исследуемой реализации не осуществляется распараллеливание шагов 2 и 4 алгоритма, т.к. ожидалось, что распределение выполнения [math]2m[/math] операций по процессам не принесёт значительного выигрыша из-за издержек на пересылки множества малых порций данных, а эксперимент показал, что во всех рассмотренных случаях временные затраты на выполнение шагов 2 и 4 в совокупности не превышают [math]4 \cdot 10^{-4}[/math] секунд.
2.2 Существующие реализации алгоритма
Авторам статьи не известно о существовании хороших реализаций данного алгоритма.
3 Литература
- ↑ Абакумов М. В., Гулин А.В. Лекции по численным методам математической физики. - Москва: ИНФРА-М, 2013. - 61 с.
- ↑ Bagnara, Roberto. (2001). A Unified Proof For The Convergence Of Jacobi And Gauss-Seidel Methods. SIAM Review. 37. 10.1137/1037008.
- ↑ https://algowiki-project.org/ru/%D0%A3%D0%BC%D0%BD%D0%BE%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5_%D0%BF%D0%BB%D0%BE%D1%82%D0%BD%D0%BE%D0%B9_%D0%BD%D0%B5%D0%BE%D1%81%D0%BE%D0%B1%D0%B5%D0%BD%D0%BD%D0%BE%D0%B9_%D0%BC%D0%B0%D1%82%D1%80%D0%B8%D1%86%D1%8B_%D0%BD%D0%B0_%D0%B2%D0%B5%D0%BA%D1%82%D0%BE%D1%80_(%D0%BF%D0%BE%D1%81%D0%BB%D0%B5%D0%B4%D0%BE%D0%B2%D0%B0%D1%82%D0%B5%D0%BB%D1%8C%D0%BD%D1%8B%D0%B9_%D0%B2%D0%B5%D1%89%D0%B5%D1%81%D1%82%D0%B2%D0%B5%D0%BD%D0%BD%D1%8B%D0%B9_%D0%B2%D0%B0%D1%80%D0%B8%D0%B0%D0%BD%D1%82)#.D0.A0.D0.B5.D1.81.D1.83.D1.80.D1.81_.D0.BF.D0.B0.D1.80.D0.B0.D0.BB.D0.BB.D0.B5.D0.BB.D0.B8.D0.B7.D0.BC.D0.B0_.D0.B0.D0.BB.D0.B3.D0.BE.D1.80.D0.B8.D1.82.D0.BC.D0.B0