Библиотека алгоритмов: различия между версиями
Перейти к навигации
Перейти к поиску
| [непроверенная версия] | [непроверенная версия] |
| Строка 61: | Строка 61: | ||
На рисунках представлено изображение графа алгоритма без входных и выходных данных для случая перемножения двух квадратных матриц порядка 3</br></br></br></br></br></br></br></br></br></br></br> | На рисунках представлено изображение графа алгоритма без входных и выходных данных для случая перемножения двух квадратных матриц порядка 3</br></br></br></br></br></br></br></br></br></br></br> | ||
| − | ==''' | + | =='''НАХОЖДЕНИЕ СУММЫ ЭЛЕМЕНТОВ МАССИВА СДВАИВАНИЕМ'''== |
| − | [[Файл: | + | [[Файл:3_XYprojection.jpg|мини|XY projection]] |
| − | |||
| − | |||
=====Ссылка на описание в энциклопедии AlgoWiki:===== | =====Ссылка на описание в энциклопедии AlgoWiki:===== | ||
| − | [https://algowiki-project.org/ru/ | + | [https://algowiki-project.org/ru/Нахождение_суммы_элементов_массива_сдваиванием Нахождение суммы элементов массива сдваиванием]</br> |
=====Реализация алгоритма на Си:===== | =====Реализация алгоритма на Си:===== | ||
| − | for ( int i= | + | for(int i=1;i<=h;i++)</br> |
| − | : for (int j=0; j< | + | : for(int j=0;j<arr_size;j++)</br> |
| − | + | :: if(j<(arr_size/(pow(2,i))))</br> | |
| − | :: | + | ::: arr[j]=arr[j*2]+arr[2*j+1]; </br> |
| − | |||
| − | ::: | ||
| − | |||
=====Описание алгоритма на Algolang:===== | =====Описание алгоритма на Algolang:===== | ||
<algo></br> | <algo></br> | ||
: <params></br> | : <params></br> | ||
| − | + | :: <param name="n" type="int" value="8"></param></br> | |
| − | :: <param name="n" type="int" value=" | + | :: <param name="h" type="int" value="3"></param></br> |
| − | :: <param name=" | ||
: </params></br></br> | : </params></br></br> | ||
| − | : <block | + | : <block dims="2"></br> |
| − | :: <arg name="i" val=" | + | :: <arg name="i" val="0..h"></arg></br> |
| − | :: <arg name="j" val="1.. | + | :: <arg name="j" val="1..n"></arg></br> |
| − | :: < | + | :: <vertex condition="(i<>0)and(j<=(n/(2^i)))" type="1"></br> |
| − | :: | + | ::: <in src="i-1,j*2-1"></in></br> |
| − | ::: <in src="i,j | + | ::: <in src="i-1,j*2"></in></br> |
:: </vertex></br> | :: </vertex></br> | ||
: </block></br> | : </block></br> | ||
</algo></br> | </algo></br> | ||
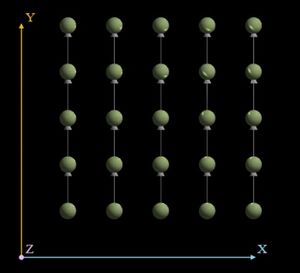
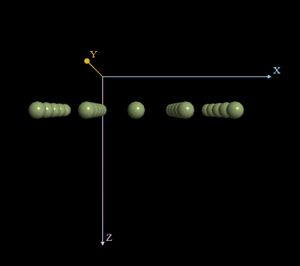
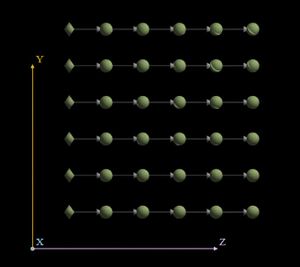
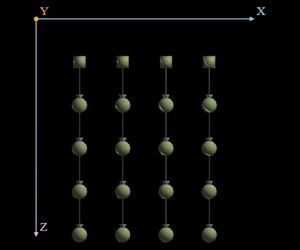
| − | На | + | На рисунке изображён граф алгоритма. В данном случае выполнено суммирование 8 элементов массива. Вершины, соответствующие входным данным, обозначены октаэдром.</br></br></br></br></br></br></br></br></br></br></br></br></br></br></br></br></br></br></br></br></br> |
Версия 01:29, 3 мая 2021
Содержание
1 УМНОЖЕНИЕ МАТРИЦЫ НА ВЕКТОР
1.1 Ссылка на описание в энциклопедии AlgoWiki:
Умножение плотной неособенной матрицы на вектор
1.2 Реализация алгоритма на Си:
for(int i = 0; i < size; i++)
- for(int j = 0; j < size ; j++)
- vec_out[i] += matrix[i][j] * vec _in[j];
- vec_out[i] += matrix[i][j] * vec _in[j];
1.3 Описание алгоритма на Algolang:
<algo>
- <params>
- <param name="size" type="int" value="5"></param>
- <param name="size" type="int" value="5"></param>
- </params>
- <block dims="2">
- <arg name="i" val="0..size-1"></arg>
- <arg name="j" val="1..size"></arg>
- <vertex condition="" type="2">
- <in src="i,j-1"></in>
- <in src="i,j-1"></in>
- </vertex>
- <arg name="i" val="0..size-1"></arg>
- </block>
</algo>
На рисунках представлен результат для матрицы размером 5*5 и вектора длины 5
2 ПЕРЕМНОЖЕНИЕ МАТРИЦ
2.1 Ссылка на описание в энциклопедии AlgoWiki:
Перемножение плотных неособенных матриц
2.2 Реализация алгоритма на Си:
for ( int i=0; i<size_1_str;i++)
- for (int j=0; j<size_2_col;j++)
- {
- matrix_out[i][j]=0;
- for(int k=0; k<size_common;k++)
- matrix_out[i][j]+=matrix_1[i][k]*matrix_2[k][j];
- matrix_out[i][j]+=matrix_1[i][k]*matrix_2[k][j];
- matrix_out[i][j]=0;
- }
2.3 Описание алгоритма на Algolang:
<algo>
- <params>
- <param name="m" type="int" value="3"></param>
- <param name="n" type="int" value="3"></param>
- <param name="l" type="int" value="3"></param>
- <param name="m" type="int" value="3"></param>
- </params>
- <block id="1" dims="3">
- <arg name="i" val="1..m"></arg>
- <arg name="j" val="1..l"></arg>
- <arg name="k" val="1..n"></arg>
- <vertex condition="k<>1" type="3">
- <in src="i,j,k-1"></in>
- <in src="i,j,k-1"></in>
- </vertex>
- <arg name="i" val="1..m"></arg>
- </block>
</algo>
На рисунках представлено изображение графа алгоритма без входных и выходных данных для случая перемножения двух квадратных матриц порядка 3
3 НАХОЖДЕНИЕ СУММЫ ЭЛЕМЕНТОВ МАССИВА СДВАИВАНИЕМ
3.1 Ссылка на описание в энциклопедии AlgoWiki:
Нахождение суммы элементов массива сдваиванием
3.2 Реализация алгоритма на Си:
for(int i=1;i<=h;i++)
- for(int j=0;j<arr_size;j++)
- if(j<(arr_size/(pow(2,i))))
- arr[j]=arr[j*2]+arr[2*j+1];
- arr[j]=arr[j*2]+arr[2*j+1];
- if(j<(arr_size/(pow(2,i))))
3.3 Описание алгоритма на Algolang:
<algo>
- <params>
- <param name="n" type="int" value="8"></param>
- <param name="h" type="int" value="3"></param>
- <param name="n" type="int" value="8"></param>
- </params>
- <block dims="2">
- <arg name="i" val="0..h"></arg>
- <arg name="j" val="1..n"></arg>
- <vertex condition="(i<>0)and(j<=(n/(2^i)))" type="1">
- <in src="i-1,j*2-1"></in>
- <in src="i-1,j*2"></in>
- <in src="i-1,j*2-1"></in>
- </vertex>
- <arg name="i" val="0..h"></arg>
- </block>
</algo>
На рисунке изображён граф алгоритма. В данном случае выполнено суммирование 8 элементов массива. Вершины, соответствующие входным данным, обозначены октаэдром.