Lanczos, MPI, OpenMP

Основные авторы описания: Волков Н.И..

1 Ссылки

Используемая реализация алгоритма Реализация алгоритма гибридная, использует как MPI версии 2.2 (использование MPI_IN_PLACE), так и OpenMP.

3 Масштабируемость алгоритма и его реализации

3.2 Масштабируемость реализации алгоритма

Указанный код компилировался с помощью компилятора IBM (mpixlcxx_r) с опцией -qsmp=omp (она включает в себя оптимизацию -O2). Реализация алгоритма полностью собственная и не использует встроенные библиотеки.

Для проверки масштабируемости алгоритма из реализации была исключена непосредственно задача поиска собственных значений матрицы [math]T_{j}[/math] на каждой итерации, так как это является предметом отдельных статей (QR-алгоритм, метод «Разделяй-и-властвуй», итерации Арнольди и.т.д.). Таким образом, проверяемая на масштабируемость задача сводится к итерационному вычислению коэффициентов матрицы [math]T_{j}[/math]. Матрица [math]A[/math] в рассматриваемой реализации хранится построчно и построчно же разделяется между процессорами. Также в целях исключения влияния недетерминированности алгоритма этот процесс изменен так, что при вычислении всех ненулевых собственных значений матрицы [math]A[/math] работа алгоритма продолжается над фиктивными данными, пока не будет завершено заранее заданное число итераций. При этом в реализации используется OpenMP для распараллеливания в пределах одного узла.

Рис. 3: Производительность алгоритма для указанных значений размера задачи и числа MPI процессов (по 4 OpenMP нити каждый). Потенциальная максимальная производительность, которая может быть достигнута - 13.6 GFLOPS на 1 MPI процесс. Тогда, например, эффективность вычислений на 100 процессах при размере задачи 4000[math]{\cdot}[/math]4000 составляет приблизительно 14.33%

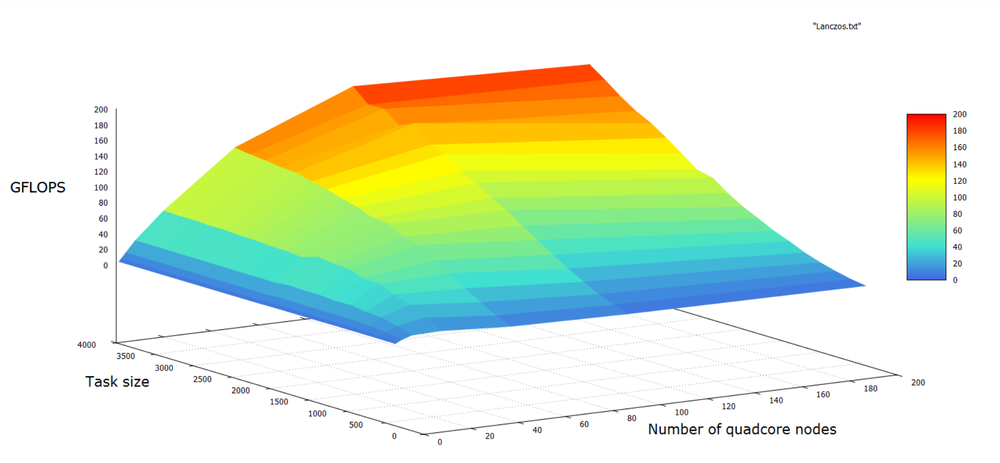
Набор изменяемых параметров запуска реализации алгоритма и границы значений параметров алгоритма:

• Число MPI процессов [1 : 200]
• Число OpenMP нитей [1 : 4] (Запуск с 1 OpenMP нитью производился только для 1 MPI процесса, ускорение замерялось относительно этого запуска).
• Размерность матрицы [400 : 4000]

Эффективность выполнения реализации алгоритма:

• Минимальная эффективность - <1% (неактуально, так как в исследовании достигнут предел масштабируемости алгоритма).
• Максимальная эффективность - ~30% (получается на 2-8 процессов при ~640000 ячеек матрицы на процесс; в случае 8 процессов это входная матрица 1600[math]{\cdot}[/math]1600).

Оценка масштабируемости:

• По числу процессов - при увеличении числа процессов эффективность уменьшается на всей области рассмотренных значений, но не слишком интенсивно. Это связано с небольшим объёмом пересылок данных, реализованных через достаточно эффективные операции редукции.
• По размеру задачи - при увеличении размера задачи эффективность вычислений вначале кратковременно возрастает, но затем начинает относительно равномерно убывать на всей рассматриваемой области.
• По двум направлениям - при рассмотрении увеличения, как вычислительной сложности, так и числа процессов по всей рассмотренной области значений наибольшая эффективность наблюдается при соответствии числа процессов и размера задачи. По этой "диагонали" эффективность вначале кратковременно возрастает, затем начинает убывать.

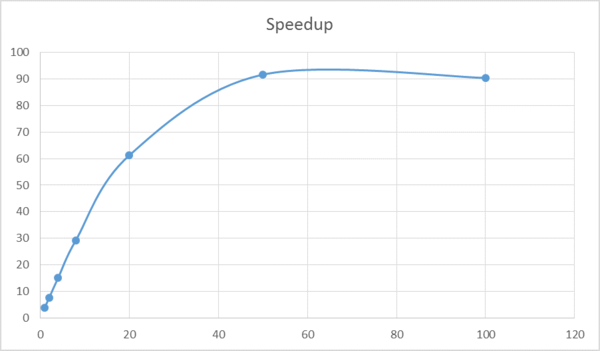
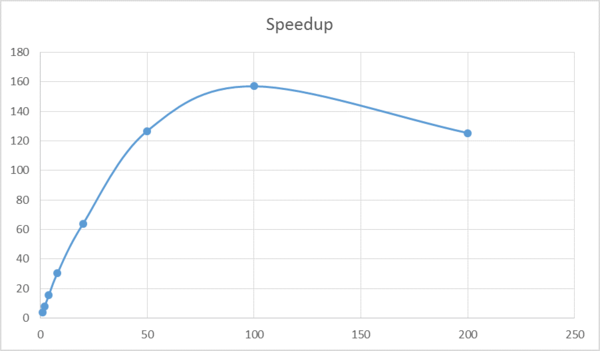
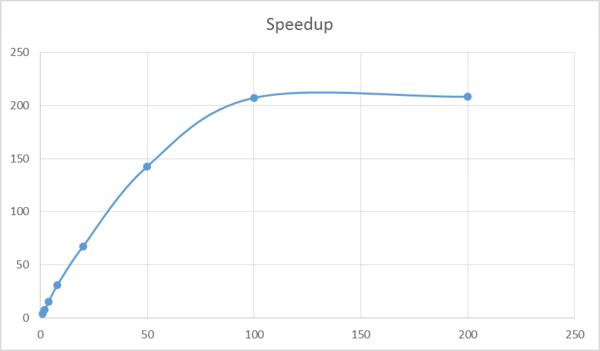
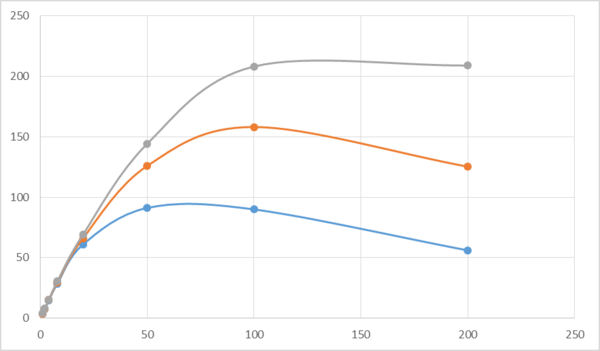
Интересно, что для разного числа процессоров положительные скачки производительности (зачастую - довольно заметные) имеют место на разных объёмах входных данных.

Далее приводятся графики ускорения программы для разных объёмов входных данных. Ускорение считалось относительно варианта с 1 MPI процессом без дальнейшнего распараллеливания посредством OpenMP. На оси абсцисс отмечается число MPI процессов, число OpenMP нитей во всех случаях равно четырём.

Рис. 4: Ускорение для размера задачи 2000[math]{\cdot}[/math]2000

Рис. 5: Ускорение для размера задачи 3000[math]{\cdot}[/math]3000

Рис. 6: Ускорение для размера задачи 4000[math]{\cdot}[/math]4000

Рис. 6: Сравнение ускорения для различных размеров задачи

Каждая "quadcore node" - это 1 узел системы BG/P, содержащий 4 микропроцессорных ядра IBM PowerPC 450 c суммарной пиковой производительностью 13.6 GFLOPS на узел и 2 GB общей памяти с пропускной способностью 13.6 GB/sec.