Итерация алгоритма dqds: различия между версиями
| [непроверенная версия] | [непроверенная версия] |
| Строка 17: | Строка 17: | ||
'''Итерация алгоритма dqds'''<ref name="vla">Деммель Д. Вычислительная линейная алгебра. – М : Мир, 2001.</ref><ref name="hola">Hogben L. (ed.). Handbook of linear algebra. – CRC Press, 2006.</ref> является одним шагом [[Алгоритм dqds нахождения сингулярных чисел двухдиагональной матрицы|итерационного алгоритма для нахождения сингулярных чисел | '''Итерация алгоритма dqds'''<ref name="vla">Деммель Д. Вычислительная линейная алгебра. – М : Мир, 2001.</ref><ref name="hola">Hogben L. (ed.). Handbook of linear algebra. – CRC Press, 2006.</ref> является одним шагом [[Алгоритм dqds нахождения сингулярных чисел двухдиагональной матрицы|итерационного алгоритма для нахождения сингулярных чисел | ||
двухдиагональной матрицы]]. Основные вычисления алгоритма dqds приходятся именно на внутреннюю итерацию. Внешняя часть алгоритма отвечает за контроль сходимости и выбор сдвигов <math>\delta,</math> что основано на довольно сложной теории и имеет различные реализации, но в то же время не влияет на вычислительные аспекты. В связи с этим dqds-итерация и [[Алгоритм dqds нахождения сингулярных чисел двухдиагональной матрицы|dqds-алгоритм]] рассматриваются отдельно. | двухдиагональной матрицы]]. Основные вычисления алгоритма dqds приходятся именно на внутреннюю итерацию. Внешняя часть алгоритма отвечает за контроль сходимости и выбор сдвигов <math>\delta,</math> что основано на довольно сложной теории и имеет различные реализации, но в то же время не влияет на вычислительные аспекты. В связи с этим dqds-итерация и [[Алгоритм dqds нахождения сингулярных чисел двухдиагональной матрицы|dqds-алгоритм]] рассматриваются отдельно. | ||
| + | |||
| + | Для понимания dqds-итерации полезно рассмотреть кратко её вывод, относительно точно отражающий и историю возникновения алгоритма (подробности можно найти в <ref name="vla">). | ||
| + | За основу dqds-алгоритма удобно взять так называемую LR-итерацию, предшествующую хорошо-известной QR-итерации. | ||
=== Математическое описание алгоритма === | === Математическое описание алгоритма === | ||
Версия 02:51, 26 мая 2016
| Алгоритм dqds нахождения сингулярных чисел двухдиагональной матрицы | |
| Последовательный алгоритм | |
| Последовательная сложность | [math]5n-4[/math] |
| Объём входных данных | [math]2n[/math] |
| Объём выходных данных | [math]2n[/math] |
| Параллельный алгоритм | |
| Высота ярусно-параллельной формы | [math]4n-3[/math] |
| Ширина ярусно-параллельной формы | [math]2[/math] |
Основные авторы описания: А.Ю.Чернявский
1 Свойства и структура алгоритмов
1.1 Общее описание алгоритма
Итерация алгоритма dqds[1][2] является одним шагом итерационного алгоритма для нахождения сингулярных чисел двухдиагональной матрицы. Основные вычисления алгоритма dqds приходятся именно на внутреннюю итерацию. Внешняя часть алгоритма отвечает за контроль сходимости и выбор сдвигов [math]\delta,[/math] что основано на довольно сложной теории и имеет различные реализации, но в то же время не влияет на вычислительные аспекты. В связи с этим dqds-итерация и dqds-алгоритм рассматриваются отдельно.
Для понимания dqds-итерации полезно рассмотреть кратко её вывод, относительно точно отражающий и историю возникновения алгоритма (подробности можно найти в Ошибка цитирования Отсутствует закрывающий тег </ref>.
1.2 Последовательная сложность алгоритма
Для выполнения одной итерации dqds необходимо выполнить:
- [math]n-1[/math] делений,
- [math]2n-2[/math] умножений,
- [math]2n-1[/math] сложений/вычитаний.
Таким образом одна dqds-итерация имеет линейную сложность.
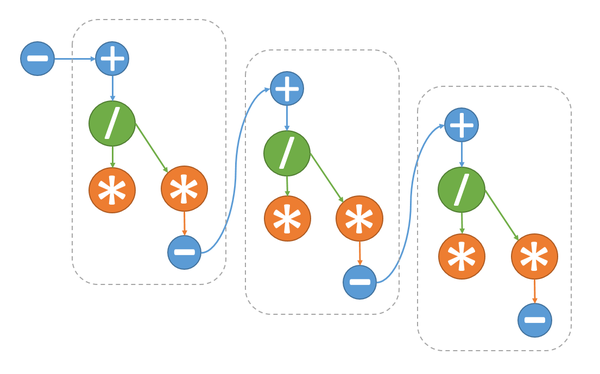
1.3 Информационный граф
1.4 Ресурс параллелизма алгоритма
Как видно из информационного графа алгоритма, на каждом шаге основного цикла возможно лишь параллельное выполнение операции умножения (2.2) и умножения+сложения (2.4). Это позволяет сократить число ярусов на одной итерации цикла c 5 до 4, а общее число ярусов алгоритма с 5n-4 до 4n-3. Ярусы с операциями умножения состоят из двух операций, остальные же из одной.
1.5 Входные и выходные данные алгоритма
Входные данные: Квадраты элементов основной и верхней побочной диагонали двухдиагональной матрицы (вектора [math]q[/math] длины n и [math]e[/math] длины n-1), а также параметр сдвига [math]\delta[/math].
Объём входных данных: [math]2n[/math].
Выходные данные: Квадраты элементов основной и верхней побочной диагонали выходной двухдиагональной матрицы.
Объём выходных данных: [math]2n-1[/math].
1.6 Свойства алгоритма
Соотношение последовательной и параллельной сложности при наличии возможности параллельного выполнения операций умножения составляет [math]\frac{5n-4}{4n-3}[/math], т.е. алгоритм плохо распараллеливается.
Вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных - константа.
Описываемый алгоритм является полностью детерминированным.
2 Программная реализация алгоритмов
2.1 Особенности реализации последовательного алгоритма
Алгоритм на языке Matlab может быть записать так:
d = q(1)-delta;
for j = 1:n-1
q(j)=d+e(j);
t=q(j+1)/q(j);
e(j) = e(j)*t;
d = d*t-delta;
end
q(n) = d;
2.2 Локальность данных и вычислений
Легко видеть, что локальность данных высока. Её легко повысить, размещая рядом соответствующие элементы массивов e и q, однако, это не оказывает существенного влияния на производительность в силу константного количества операций относительно объема обрабатываемых данных.
2.3 Возможные способы и особенности параллельной реализации алгоритма
Итерация dqds практически полностью последовательна. Единственная возможность - одновременное выполнение операции умножения (2.3) и опрерации (2.4) умножения и сложения, что дает небольшой выигрыш в производительности.
2.4 Масштабируемость алгоритма и его реализации
Алгоритм не является масштабируемым, максимального эффекта ускорения можно добиться на двух независимых процессорах.
2.5 Выводы для классов архитектур
Эффективное выполнение алгоритма возможно только на вычислительных устройствах с одним или двумя ядрами.
2.6 Существующие реализации алгоритма
Перечень реализаций приведен на странице алгоритма dqds.