Участник:DenisAnuprienko/Метод Штрассена

Основные авторы описания: Д.В.Ануприенко.

Общая схема описания алгоритмов имеет следующий вид:

1 Свойства и структура алгоритмов

1.1 Общее описание алгоритма

Метод Штрассена предназначен для умножения матриц. Здесь будет рассмотрен вариант метода, который можно применять к квадратным матрицам размера [math]N = 2^n[/math]. В таком случае две матрицы можно умножить быстрее, чем за [math]O(N^3)[/math].

1.2 Математическое описание алгоритма

Пусть имеются две матрицы [math]A, B \in \mathbb{R}^{N\times N}[/math]. Представим их в блочном виде: [math] A = \begin{bmatrix} A_{11} & A_{12}\\ A_{21} & A_{22}\\ \end{bmatrix}, B = \begin{bmatrix} B_{11} & B_{12}\\ B_{21} & B_{22}\\ \end{bmatrix}. [/math] При обычном умножении матриц пришлось бы совершить 8 умножений подматриц порядка [math]N/2[/math]. В методе Штрассена предлагается обойтись всего 7 умножениями. Находятся 7 вспомогательных подматриц [math]M_1, ..., M_7[/math] по следующим формулам:
[math] M_1 = (A_{11} + A_{22})(B_{11} + B_{22}) [/math]
[math] M_2 = (A_{21} + A_{22})B_{11} [/math]
[math] M_3 = A_{11}(B_{12} - B_{22}) [/math]
[math] M_4 = A_{22}(B_{21} - B_{11}) [/math]
[math] M_5 = (A_{11} + A_{12})B_{22} [/math]
[math] M_6 = (A_{21} - A_{22})(B_{11} + B_{12}) [/math]
[math] M_7 = (A_{12} - A_{22})(B_{21} + B_{22}) [/math]

После этого матрица [math]C[/math], являющаяся произведением [math]A[/math] и [math]B[/math], находится по формулам
[math] C_{11} = M_1 + M_4 - M_5 + M_7 [/math]
[math] C_{12} = M_3 + M_5 [/math]
[math] C_{21} = M_2 + M_4 [/math]
[math] C_{22} = M_1 - M_2 + M_3 + M_6 [/math]

Если и умножения подматриц, необходимые для нахождения [math]M_i[/math], проводить по такой же схеме, получается рекурсивный алгоритм. Всего в нем понадобится выполнить [math]O(7^{log_2N}) = O(N^{log_27}) \approx O(N^{2.81})[/math] умножений. На практике рекурсию можно не разворачивать до конца, а использовать обычное умножение уже на матрицах размера 512.

[math][/math]

1.3 Вычислительное ядро алгоритма

Основное время работы алгоритма приходится на формирование множителей для умножения подматриц, рекурсивные вызовы и умножение матриц обычным методом в конце рекурсии.

1.5 Схема реализации последовательного алгоритма

1. Если размер матриц меньше или равен некоторого числа [math]N_{min}[/math], умножить их обычным способом.
2. Иначе
   1. Сформировать множители для матрицы [math]M_1[/math]
   2. Применить метод Штрассена для этих множителей
   3. Сформировать множители для матрицы [math]M_2[/math]
   4. Применить метод Штрассена для этих множителей
   5. ...
   6. Сформировать множители для матрицы [math]M_7[/math]
   7. Применить метод Штрассена для этих множителей
   8. Сформировать результат из матриц [math]M_1, ..., M_7[/math].

1.6 Последовательная сложность алгоритма

Метод Штрассен позволяет сократить число умножений, поэтому оценивается именно оно. В методе Штрассена число умножений составляет [math]O(7^{log_2N}) = O(N^{log_27}) \approx O(N^{2.81})[/math].

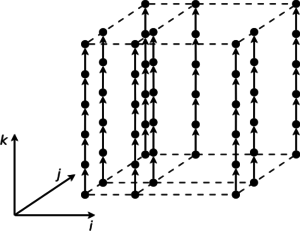
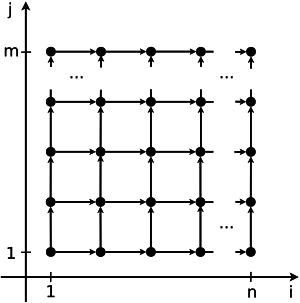
1.7 Информационный граф

Это очень важный раздел описания. Именно здесь можно показать (увидеть) как устроена параллельная структура алгоритма, для чего приводится описание и изображение его информационного графа (графа алгоритма ). Для рисунков с изображением графа будут составлены рекомендации по их формированию, чтобы все информационные графы, внесенные в энциклопедию, можно было бы воспринимать и интерпретировать одинаково. Дополнительно можно привести полное параметрическое описание графа в терминах покрывающих функций .

Интересных вариантов для отражения информационной структуры алгоритмов много. Для каких-то алгоритмов нужно показать максимально подробную структуру, а иногда важнее макроструктура. Много информации несут разного рода проекции информационного графа, выделяя его регулярные составляющие и одновременно скрывая несущественные детали. Иногда оказывается полезным показать последовательность в изменении графа при изменении значений внешних переменных (например, размеров матриц): мы часто ожидаем "подобное" изменение информационного графа, но это изменение не всегда очевидно на практике.

В целом, задача изображения графа алгоритма весьма нетривиальна. Начнем с того, что это потенциально бесконечный граф, число вершин и дуг которого определяется значениями внешних переменных, а они могут быть весьма и весьма велики. В такой ситуации, как правило, спасают упомянутые выше соображения подобия, делающие графы для разных значений внешних переменных "похожими": почти всегда достаточно привести лишь один граф небольшого размера, добавив, что графы для остальных значений будут устроены "точно также". На практике, увы, не всегда все так просто, и здесь нужно быть аккуратным.

Далее, граф алгоритма - это потенциально многомерный объект. Наиболее естественная система координат для размещения вершин и дуг информационного графа опирается на структуру вложенности циклов в реализации алгоритма. Если глубина вложенности циклов не превышает трех, то и граф размещается в привычном трехмерном пространстве, однако для более сложных циклических конструкций с глубиной вложенности 4 и больше необходимы специальные методы представления и изображения графов.

В данном разделе AlgoWiki могут использоваться многие интересные возможности, которые еще подлежат обсуждению: возможность повернуть граф при его отображении на экране компьютера для выбора наиболее удобного угла обзора, разметка вершин по типу соответствующим им операций, отражение ярусно-параллельной формы графа и другие. Но в любом случае нужно не забывать главную задачу данного раздела - показать информационную структуру алгоритма так, чтобы стали понятны все его ключевые особенности, особенности параллельной структуры, особенности множеств дуг, участки регулярности и, напротив, участки с недерминированной структурой, зависящей от входных данных.

На рис.1 показана информационная структура алгоритма умножения матриц, на рис.2 - информационная структура одного из вариантов алгоритма решения систем линейных алгебраических уравнений с блочно-двухдиагональной матрицей.

Рис.1. Информационная структура алгоритма умножения матриц

Рис.2. Информационная структура одного из вариантов алгоритма решения систем линейных алгебраических уравнений с блочно-двухдиагональной матрицей

1.8 Ресурс параллелизма алгоритма

Умножения, которые необходимы для нахождения матриц [math]M_1, ..., M_7[/math], можно провести параллельно. Их можно предоставить 7 узлам (1 хозяин, который раздает задания 6 рабочим и получает результаты, а также работает вместе с ними) или 8 узлам (1 хозяин, который раздает задания 7 рабочим и получает результаты).

1.9 Входные и выходные данные алгоритма

Нет никаких предположений насчет структуры матриц. Предполагается, что это обычные плотные матрицы. Они хранятся в виде одномерного массива, что позволяет легко выделять из них подматрицы.

1.10 Свойства алгоритма

• Алгоритм устойчив
• Алгоритм детерминирован

2 Программная реализация алгоритма

2.2 Локальность данных и вычислений

Вопросы локальности данных и вычислений не часто изучаются на практике, но именно локальность определяет эффективность выполнения программ на современных вычислительных платформах . В данном разделе приводятся оценки степени локальности данных и вычислений в программе, причем рассматривается как временна́я, так и пространственная локальность. Отмечаются позитивные и негативные факты, связанные с локальностью, какие ситуации и при каких условиях могут возникать. Исследуется, как меняется локальность при переходе от последовательной реализации к параллельной. Выделяются ключевые шаблоны взаимодействия программы, реализующей описываемый алгоритм, с памятью. Отмечается возможная взаимосвязь между используемыми конструкциями языков программирования и степенью локальности, которыми обладают результирующие программы.

Отдельно приводятся профили взаимодействия с памятью для вычислительных ядер и ключевых фрагментов. Если из-за большого числа обращений по общему профилю сложно понять реальную специфику взаимодействия программ с памятью, то проводится последовательная детализация и приводится серия профилей более мелкого масштаба.

На рис.3 и рис.4 показаны профили обращения в память для программ, реализующих разложение Холецкого и быстрое преобразование Фурье, по которым хорошо видна разница свойств локальности у данных алгоритмов.

Рис.3 Реализация метода Холецкого. Общий профиль обращений в память

Рис.4 Нерекурсивная реализация БПФ для степеней двойки. Общий профиль обращений в память

2.3 Возможные способы и особенности параллельной реализации алгоритма

Раздел довольно обширный, в котором должны быть описаны основные факты и положения, формирующие параллельную программу. К их числу можно отнести:

• представленный иерархически ресурс параллелизма, опирающийся на структуру циклических конструкций и на граф вызовов программы;
• комбинацию (иерархию) массового параллелизма и параллелизма конечного;
• возможные способы распределения операций между процессами/нитями;
• возможные способы распределения данных;
• оценку количества операций, объёма и числа пересылок данных (как общего числа, так и в пересчёте на каждый параллельный процесс);

и другие.

В этом же разделе должны быть даны рекомендации или сделаны комментарии относительно реализации алгоритма с помощью различных технологий параллельного программирования: MPI, OpenMP, CUDA или использования директив векторизации.

2.4 Масштабируемость алгоритма и его реализации

Задача данного раздела - показать пределы масштабируемости алгоритма на различных платформах. Очень важный раздел. Нужно выделить, описать и оценить влияние точек барьерной синхронизации, глобальных операций, операций сборки/разборки данных, привести оценки или провести исследование сильной и слабой масштабируемости алгоритма и его реализаций.

Масштабируемость алгоритма определяет свойства самого алгоритма безотносительно конкретных особенностей используемого компьютера. Она показывает, насколько параллельные свойства алгоритма позволяют использовать возможности растущего числа процессорных элементов. Масштабируемость параллельных программ определяется как относительно конкретного компьютера, так и относительно используемой технологии программирования, и в этом случае она показывает, насколько может вырасти реальная производительность данного компьютера на данной программе, записанной с помощью данной технологии программирования, при использовании бóльших вычислительных ресурсов (ядер, процессоров, вычислительных узлов).

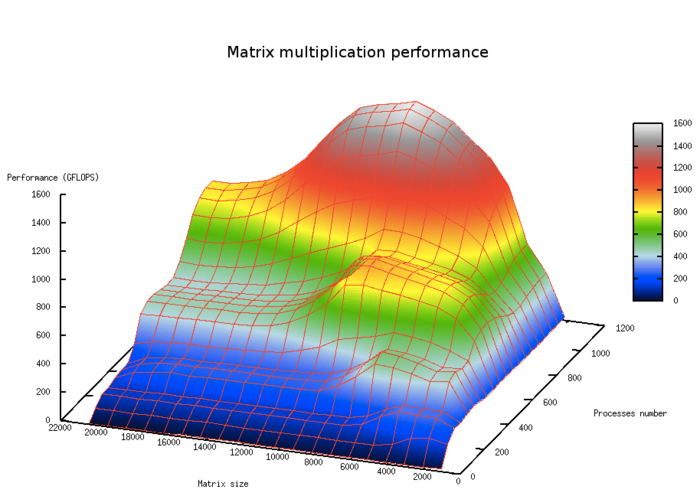
Ключевой момент данного раздела заключается в том, чтобы показать реальные параметры масштабируемости программы для данного алгоритма на различных вычислительных платформах в зависимости от числа процессоров и размера задачи . При этом важно подобрать такое соотношение между числом процессоров и размером задачи, чтобы отразить все характерные точки в поведении параллельной программы, в частности, достижение максимальной производительности, а также тонкие эффекты, возникающие, например, из-за блочной структуры алгоритма или иерархии памяти.

На рис.5. показана масштабируемость классического алгоритма умножения плотных матриц в зависимости от числа процессоров и размера задачи. На графике хорошо видны области с большей производительностью, отвечающие уровням кэш-памяти.

Рис.5 Масштабируемость классического алгоритма умножения плотных матриц в зависимости от числа процессоров и размера задачи

2.5 Динамические характеристики и эффективность реализации алгоритма

Это объемный раздел AlgoWiki, поскольку оценка эффективности реализации алгоритма требует комплексного подхода , предполагающего аккуратный анализ всех этапов от архитектуры компьютера до самого алгоритма. Основная задача данного раздела заключается в том, чтобы оценить степень эффективности параллельных программ, реализующих данный алгоритм на различных платформах, в зависимости от числа процессоров и размера задачи. Эффективность в данном разделе понимается широко: это и эффективность распараллеливания программы, это и эффективность реализации программ по отношению к пиковым показателям работы вычислительных систем.

Помимо собственно показателей эффективности, нужно описать и все основные причины, из-за которых эффективность работы параллельной программы на конкретной вычислительной платформе не удается сделать выше. Это не самая простая задача, поскольку на данный момент нет общепринятой методики и соответствующего инструментария, с помощью которых подобный анализ можно было бы провести. Требуется оценить и описать эффективность работы с памятью (особенности профиля взаимодействия программы с памятью), эффективность использования заложенного в алгоритм ресурса параллелизма, эффективность использования коммуникационной сети (особенности коммуникационного профиля), эффективность операций ввода/вывода и т.п. Иногда достаточно интегральных характеристик по работе программы, в некоторых случаях полезно показать данные мониторинга нижнего уровня, например, по загрузке процессора, кэш-промахам, интенсивности использования сети Infiniband и т.п. Хорошее представление о работе параллельной MPI-программы дают данные трассировки, полученные, например, с помощью системы Scalasca.

2.6 Выводы для классов архитектур

В данный раздел должны быть включены рекомендации по реализации алгоритма для разных классов архитектур. Если архитектура какого-либо компьютера или платформы обладает специфическими особенностями, влияющими на эффективность реализации, то это здесь нужно отметить.

На практике это сделать можно по-разному: либо все свести в один текущий раздел, либо же соответствующие факты сразу включать в предшествующие разделы, где они обсуждаются и необходимы по смыслу. В некоторых случаях, имеет смысл делать отдельные варианты всей части II AlgoWiki применительно к отдельным классам архитектур, оставляя общей машинно-независимую часть I. В любом случае, важно указать и позитивные, и негативные факты по отношению к конкретным классам. Можно говорить о возможных вариантах оптимизации или даже о "трюках" в написании программ, ориентированных на целевые классы архитектур.

2.7 Существующие реализации алгоритма

Для многих пар алгоритм+компьютер уже созданы хорошие реализации, которыми можно и нужно пользоваться на практике. Данный раздел предназначен для того, чтобы дать ссылки на основные существующие последовательные и параллельные реализации алгоритма, доступные для использования уже сейчас. Указывается, является ли реализация коммерческой или свободной, под какой лицензией распространяется, приводится местоположение дистрибутива и имеющихся описаний. Если есть информация об особенностях, достоинствах и/или недостатках различных реализаций, то это также нужно здесь указать. Хорошими примерами реализации многих алгоритмов являются MKL, ScaLAPACK, PETSc, FFTW, ATLAS, Magma и другие подобные библиотеки.