Участник:Антон Тодуа/Partitioning Around Medoids (PAM)

Основные авторы описания: Тодуа А.Р., Гусева Ю.В.

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

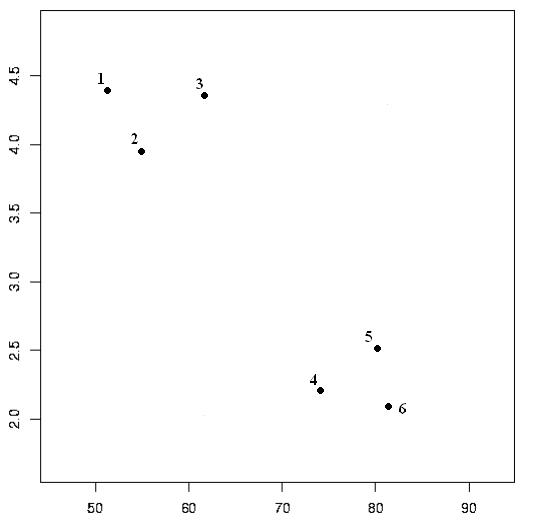
Кластеризация – это процесс автоматического разбиения некоторого множества элементов на группы(кластеры) на основе степени их схожести. Для лучшего осознания, что такое кластер, рассмотрим пример.

Рисунок 1.

В этом небольшом наборе данных четко выделяются две различные группы объектов,а именно: {1, 2, 3} и (4, 5, 6}. Такие группы и называются кластерами, и обнаружить их является целью кластерного анализа.

Таким образом, у кластера можно выделить два признака

● внутренняя однородность;

● внешняя изолированность.

Для чего используется кластеризация?

● Группировка объектов

● Распознавание образов

● Выявление структуры данных

● Сжатие данных

Для чего используется кластеризация?

● классификация результатов поиска (nigma, yippy,quintura)

● автоматическое построение каталогов

● работа только с несколькими представителями кластеров

● сегментация изображений — компьютерная графика

● кластеризация документов, таблиц и др.данных

● выделение групп клиентов, покупателей,товаров для разработки отдельных стратегий

Очевидно, что спектр применений кластерного анализа очень широк: в археологии, медицине, психологии, химии, биологии, государственном управлении, филологии, антропологии, маркетинге, социологии и других дисциплинах.

По типу обработки данных можно выделить два класса методов:

Иерархические методы:

   Агломеративные методы AGNES (Agglomerative Nesting):

   - CURE;

   - ROCK;

   - CHAMELEON и т.д.

  Дивизимные методы DIANA (Divisive Analysis):

   - BIRCH;

   - MST и т.д.

Неиерархические методы.

  Итеративные
  - К-средних (k-means)
  - PAM (k-means + k-medoids)
  - CLOPE
  - LargeItem и т.д. 

Самый распространённый вариант реализации [math]k[/math]-medoids называется PAM (Partitioning Around Medoids). Он представляет собой «жадный» алгоритм с очень неэффективной эвристикой. Данный метод был предложен Кауфманом в 1987 году.

Алгоритм начинается с выбора набора данных, состоящих из медоидов и остальных объектов. После выбора [math]k[/math] произвольных объектов в качестве медоидов, необходимо для каждой пары [math]{x_i}[/math] и [math]{m_k}[/math] вычислить значение [math]S({x_{i}}{m_{k}})[/math]. По ходу выполнения алгоритма происходит итеративная замена одного из медоидов [math]x_i[/math] одним из остальных объектов [math]m_k[/math], если посчитанное ранее значение [math]S[/math] меньше нуля. Процесс будет повторятся, пока медоиды не стабилизируются.

PAM (Partitioning Around Medoids, 1987) • CLARA (Kaufmann & Rousseeuw, 1990) • CLARANS (Ng & Han, 1994): Randomized sampling

The PAM (Partioning Around Medoids) algorithm, also called the K-medoids algorithm

Дано: множество входной набор данных k — количество кластеров Найти:разбиение множества на кластеры

Этапы кластеризации (общий алгоритм) ● Выбор меры близости; ● Выбор алгоритма кластеризации; ● Представление полученных результатов;

1.2 Математическое описание алгоритма

В качестве исходных данных алгоритм принимает:

• Симметрическую матрицу [math]D[/math] порядка [math]N[/math] с нолями на главной диагонали для [math]N[/math] объектов кластеризации: [math]i[/math]-я строка матрицы [math]D[/math] определяет непохожесть [math]i[/math]-го объекта кластеризации на все остальные объекты
• Число кластеров [math]K[/math], при этом: [math]K \lt N[/math]

Для заданных входных данных, алгоритм выбирает [math]K[/math] объектов - медоидов (medoids) из [math]N[/math] объектов кластеризации. При этом выбор медоидов осуществляется исходя из минимизации средней непохожести (average dissimilarity) объектов и ближайшего к ним медоида. От минимизации средней непохожести можно перейти к минимизации суммы непохожестей объектов на ближайший к ним медоид, т.к. это не повлияет на выбор медоидов, но позволит не накапливать ошибки округления, возникающие в результате операции деления.

Для дальнейшего описания алгоритма введём следующие обозначения:

• [math]U[/math] – множество объектов кластеризации, не выбранных в качестве медоидов
• [math]S[/math] – множество объектов кластеризации, выбранных в качестве медоидов
• [math]C_{ij}[/math] – изменение непохожести [math]j[/math]-го объекта в результате выбора [math]i[/math]-го объекта в качестве медоида
• [math]T_{ijh}[/math] – изменение непохожести [math]j[/math]-го объекта в результате операции обмена, т.е. выбора [math]h[/math]-го объекта в качестве медоида, вместо [math]i[/math]-го объекта

Перед выполнением алгоритма множество [math]U[/math] содержит все объекты кластеризации, а множество [math]S[/math] – пусто.

Выполнение алгоритма включает в себя подготовительную стадию BUILD и итерационную стадию SWAP.

Стадия BUILD предназначена для построения начального множества медоидов и состоит в последовательном выполнении следующих шагов:

1. Добавить в множество [math]S[/math] объект, для которого сумма непохожести на все остальные объекты минимальна (самый центральный объект):

[math]S = S + \{ arg\min_{i \in U} \sum_{j \in U} d_{ij} \}[/math]

2. Выбрать ещё [math]K-1[/math] медоидов следующим образом

[math]S = S + \{ arg\max_{i \in U} \sum_{j \in U - \{i\}} C_{ij} \}[/math]

Стадия SWAP является итерационной, одна итерация состоит в попытке улучшить кластеризацию путём выполнения операции обмена, т.е. замены одного медоида на другой. На каждой итерации выполняется операция [math]arg\min_{i \in S, h \in U} \sum_{j \in U - \{h\}} T_{ijh}[/math]. Если для найденной пары [math]i \in S[/math] и [math]h \in U[/math] значение [math]\sum_{j \in U - \{h\}} T_{ijh}[/math] меньше ноля (это означает, что кластеризацию можно улучшить), то выполняется обмен [math]i[/math] и [math]h[/math] ([math]U = U - \{k\}, S = S + \{k\}[/math]), иначе дальнейшее улучшение кластеризации невозможно и алгоритм завершает свою работу.

В результате работы алгоритма множество [math]S[/math] будет содержать ровно [math]K[/math] объектов – медоидов, принадлежащих разным кластерам. Кластер объекта [math]j[/math] из множества [math]U[/math] совпадает с кластером ближайшего к нему медоида: [math]arg\min_{i \in S} d_{ij}[/math]

1.3 Вычислительное ядро алгоритма

Из математического описания алгоритма следует, что вычислительное ядро алгоритма сосредоточено в итерационной стадии SWAP. Одна итерация состоит в вычислении:

[math]arg\min_{i \in S, h \in U} \sum_{j \in U - \{h\}} T_{ijh}[/math]

Смысл этого выражения в том, что выполняется выбор такой пары медоида [math]i[/math] и объекта [math]h[/math] операция обмена которых приведёт к улучшению кластеризации или же делается вывод о невозможности такого обмена и работа алгоритма завершается.

1.4 Макроструктура алгоритма

• [math]D_{i}[/math] – непохожесть [math]i[/math]-го объекта на ближайший к нему медоид
• [math]E_{i}[/math] – непохожесть [math]i[/math]-го объекта на второй ближайший к нему медоид

Числа [math]D_{i}[/math] и [math]E_{i}[/math] могут измениться при изменениях в множествах [math]U[/math] и [math]S[/math].

2. Для каждого объекта [math]i \in U[/math] выполнить шаги 3-5

3. Для каждого объекта [math]j \in U - \{i\}[/math] вычислить [math]D_{j}[/math] и выполнить шаг 4

4. Положить [math]C_{ij} = max\{ D_{j} - d_{ij}, 0 \}[/math], мера улучшения кластеризации

5. Положить [math]g_{i} = \sum_{j \in U - \{i\}} C_{ij}[/math], улучшение от выбора [math]i[/math]-го объекта в качестве медоида

6. Выбрать объект, максимизирующий величину [math]g_{i}[/math] в качестве медоида:

[math] \begin{align} k & = arg\min_{i \in U} \sum_{j \in U} d_{ij} \\ U & = U - \{k\} \\ S & = S + \{k\} \\ \end{align} [/math]

7. Если множество [math]S[/math] содержит менее [math]K[/math] объектов (медоидов) перейти к шагу 2

8. КОНЕЦ стадии BUILD

Стадия SWAP (итерационное улучшение кластеризации):

1. Для всех возможных пар объектов [math]i \in S[/math] и [math]h \in U[/math] выполнить шаги 2-4

2. Вычислить эффект [math]T_{ih}[/math] от выполнения обмена объектов [math]i[/math] и [math]h[/math] (т.е. объект [math]i[/math] больше не выбран в качестве медоида, а объект [math]h[/math], наоборот, выбран в качестве медоида). Способ вычисления [math]T_{ih}[/math] описан ниже.

3. Положим [math](i', h') = arg\min_{i \in S, h \in U} T_{ih}[/math]

4. Если [math]T_{i'h'}[/math] больше 0 (т.е. кластеризацию можно улучшить), то выполняем обмен объектов [math]i[/math] и [math]h[/math] ([math]U = U - \{k\}, S = S + \{k\}[/math]) и переходим к шагу 1

5. КОНЕЦ стадии SWAP

1.5 Схема реализации последовательного алгоритма

В соответствии с приведённым выше математическим описанием последовательное выполнение алгоритма представляет собой выполнение стадии BUILD, а затем последовательное повторение итераций стадии SWAP до тех пор пока существует пара объектов (один из которых медоид, а другой – нет), которые можно обменять, чтобы улучшить кластер.

1.6 Последовательная сложность алгоритма

При описании последовательной сложности будем считать, что выполняется распределение [math]N[/math] объектов по [math]K[/math] кластерам. В соответствии с приведённым математическим описанием алгоритм включает в себя подготовительную стадию BUILD и итерационную стадию SWAP.

Стадия BUILD сводится к вычислению:

Одной операции [math]arg\min_{i} \sum_{j} d_{ij}[/math]
[math]K-1[/math] операций [math]arg\max_{i \in U} \sum_{j \in U - \{i\}} C_{ij}[/math]

Т.е. стадия BUILD требует:

[math]K * N^2[/math] операций сложения
[math]K * N[/math] операций сравнения (определения максимума/минимума)
Около [math]K * N^2[/math] вычислений [math]C_{ij}[/math]

Одна итерация стадии SWAP сводится к вычислению:

[math]arg\min_{i \in S, h \in U} \sum_{j \in U - \{h\}} T_{ijh}[/math]

Т.е. одна итерации стадии SWAP требует порядка:

[math]K * N^2[/math] операций сложения
[math]K * N[/math] операций сравнения (определения максимума/минимума)
[math]K * (N - K) * (N - K - 1)[/math] вычислений [math]T_{ijh}[/math]

Вычисления [math]C_{ij}[/math] и [math]T_{ijh}[/math] имеют константную сложность для любых [math]i[/math], [math]j[/math] и [math]h[/math], поэтому сложность одной итерации алгоритма определяется как [math]O(K * N^2)[/math]. Таким образом можно отнести алгоритм PAM к алгоритмам с кубической сложностью.

1.9 Входные и выходные данные алгоритма

Входные данные:

1. Матрица непохожести объектов кластеризации (dissimilarity matrix) [math]D[/math] (элементы [math]d_{ij}[/math]).
Дополнительные ограничения:
- [math]D[/math] – симметрическая матрица порядка [math]N[/math], т.е. [math]d_{ij}= d_{ji}, i, j = 1, \ldots, N[/math]
- [math]D[/math] – содержит нули на главной диагонали, т.е. [math]d_{ii}= 0, i = 1, \ldots, N[/math]
2. [math]K[/math] - число кластеров, на которое следует разбить объекты кластеризации

Объём входных данных:

[math]\frac{N (N - 1)}{2}[/math] (в силу симметричности и нулевой главной диагонали достаточно хранить только  над/поддиагональные элементы). В разных реализациях эта экономия хранения может быть выполнена разным образом. 

Выходные данные:

[math]N[/math] чисел [math]k_{1}, k_{2}, \ldots, k_{N}[/math], где [math]k_{i}[/math] - целое число, соответствующее кластеру [math]i[/math]-го объекта.

Выходными данными алгоритма также можно считать [math]K[/math] чисел, задающих номера объектов кластеризации, выделенных в качестве медоидов (medoids). Однако в большинстве случаев требуется именно определение кластеров объектов, а не поиск соответствующих медоидов.

Объём выходных данных:

[math]N[/math] (кластеры объектов кластеризации)

2 Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

PAM работает эффективно для небольших наборов данных, но не очень хорошо масштабируется для больших наборов данных