Умножение плотной матрицы на вектор

2 Программная реализация

2.2 Описание локальности данных и вычислений

2.2.2 Описание локальности реализации алгоритма

2.2.2.1 Описание структуры обращений в память и качественная оценка локальности

Рисунок 12.1. Умножение плотной матрицы на вектор. Общий профиль обращений в память

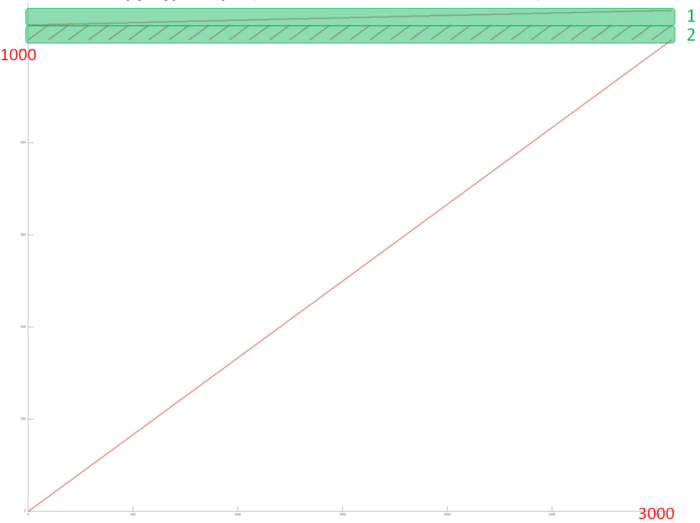
На рисунке 12.1 представлен профиль обращений в память для реализации умножения плотной матрицы на вектор. В данном алгоритме задействовано три массива. Выделенный зеленым фрагмент 1 образован обращениями к результирующему вектору; фрагмент 2 – обращениями к исходному вектору; остальные обращения (фрагмент 3) выполняются к матрице, на которую умножается исходный вектор.

Если посмотреть на исходный код, становится понятным, что каждый фрагмент устроен очень просто:

for(int i = 0; i < size; i++)
for(int j = 0; j < size; j++)
vec_out[i] += matrix[i][j] * vec_in[j];

Видно, что фрагмент 1 (обращения к массиву vec_out) состоит из последовательного перебора всех элементов вектора, только к каждому элементу происходит подряд size обращений. Во фрагменте 2 (массив vec_in) выполняется обычный последовательный перебор, который затем повторяется size раз. Фрагмент 3 также представляет собой последовательный перебор всех элементов матрицы, который выполняется только один раз.

Самой высокой локальностью обладает фрагмент 1 из-за повторяющихся подряд обращений к одним и тем же элементам. Однако фрагмент 2 также обладает высокой как пространственной, так и временной локальностью, поскольку число повторных проходов достаточно велико. Фрагмент 3, как и остальные, характеризуется высокой пространственной локальностью (из-за последовательного перебора), однако очень низкой временной локальностью – повторные обращения в нем просто отсутствуют.

2.2.2.2 Количественная оценка локальности

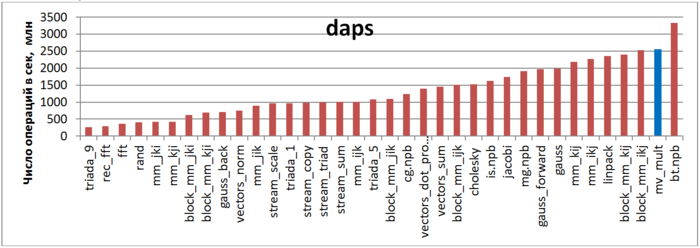
Первая оценка выполняется на основе характеристики daps, которая оценивает число выполненных обращений (чтений и записей) в память в секунду. Данная характеристика является аналогом оценки flops применительно к работе с памятью и является в большей степени оценкой производительности взаимодействия с памятью, чем оценкой локальности. Однако она служит хорошим источником информации, в том числе для сравнения с результатами по следующей характеристике cvg.

На рисунке 12.2 приведены значения daps для реализаций распространенных алгоритмов, отсортированные по возрастанию (чем больше daps, тем в общем случае выше производительность). Можно увидеть, что производительность данной программы очень высока, даже немного выше, чем производительность теста Linpack. Одна из основных причин этому – очень высокая локальность обращений к векторам.

Рисунок 12.2. Сравнение значений оценки daps

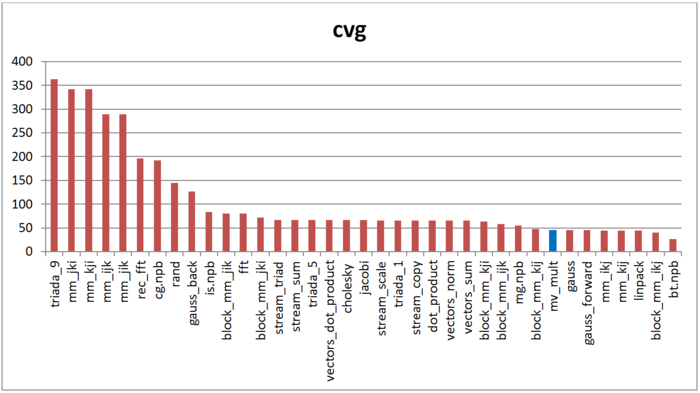
Вторая характеристика – cvg – предназначена для получения более машинно-независимой оценки локальности. Она определяет, насколько часто в программе необходимо подтягивать данные в кэш-память. Соответственно, чем меньше значение cvg, тем реже это нужно делать, тем лучше локальность.

На рисунке 12.3 приведены значения cvg для того же набора реализаций, отсортированные по убыванию (чем меньше cvg, тем в общем случае выше локальность). Можно увидеть, что, согласно данной оценке, локальность реализации умножения матрицы на вектор высока, хотя и не среди первых значений. Однако можно заметить, что полученное значение лишь совсем немного ниже оценки cvg для, например, реализации метода Гаусса или лучших вариантов перемножения матрицы.

Рисунок 12.3. Сравнение значений оценки cvg

2.4 Масштабируемость алгоритма и его реализации

2.4.2 Описание масштабируемости реализации алгоритма

Рисунок 1. Параллельная реализация произведения матрицы на вектор Максимальная производительность.

Рисунок 2. Параллельная реализация произведения матрицы на вектор Максимальная эффективность.

Набор изменяемых параметров запуска реализации алгоритма и границы значений параметров алгоритма:

• число процессоров [4 : 256]
• размерность матрицы [1024 : 51200]

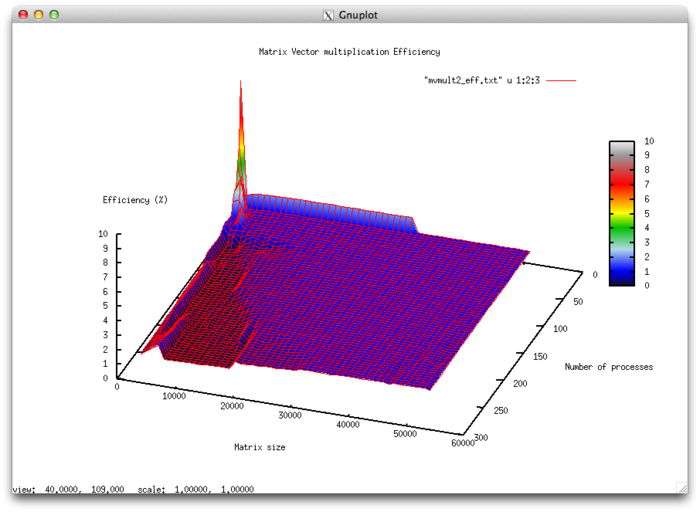
Эффективность выполнения реализации алгоритма

• Минимальная эффективность 0,02%
• Максимальная эффективность 9,55%

Оценка масштабируемости

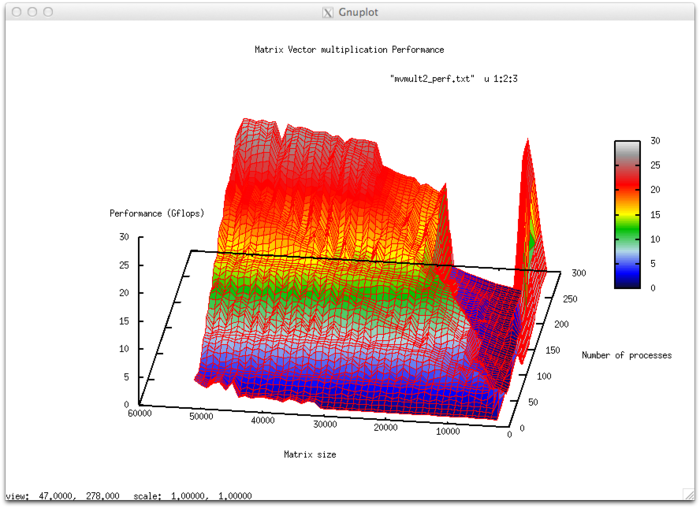
• По числу процессов: -0.01517 – при увеличении числа процессов эффективность убывает достаточно интенсивно на всей рассмотренной области изменений параметров запуска. Уменьшение эффективности на рассмотренной области работы параллельной программы звязано с увеличением числа пересылок с ростом числа процессов и как следствие ростом накладных расходов на организацию вычислений. Присутствует область, на которой при увеличении числа процессов эффективность возрастает, но при дальнейшем росте продолжает снижаться. Это объясняется декомпозицей данных, при которой наступает момент, когда размер матрицы позволяет блокам укладываться в КЭШ-память. Так же это подтверждает проявление этого явления, но со смещением по числу процессов, и при увеличении вычислительной сложности задачи.
• По размеру задачи: -0.0014 – при увеличении размера задачи эффективность в целом уменьшается по рассматриваемой области, хотя и менее интенсивно, чем при увеличении числа процессов. Снижение эффективности объясняется тем, что при росте вычислительной сложности существенно возрастают объемы передаваемых данных. Присутствует область возрастания эффективности, на всех рассмотренных размерах матрицы. Это объясняется тем, что при малом размере задачи данные хорошо укладываются в КЭШ память, что приводит к высокой эффективности работы приложения при малом размере задачи. При дальнейшем увеличении размера эффективность уменьшается при выходе за границы КЭШ-памяти.
• По двум направлениям: -0.0001546 – при рассмотрении увеличения, как вычислительной сложности, так и числа процессов по всей рассмотренной области значений уменьшается, интенсивность уменьшения эффективности не очень высока. В совокупности с тем фактом, что разница между максимальной и минимальной эффективностью на рассмотренной области значений параметров составляет почти 25% говорит о том, что уменьшение эффективности по всей области довольно равномерное, но интенсивно лишь в не очень больших участках по площади. На остальной области значений параметров изменения эффективности не столь значительны и находятся на приблизительно одном и том же уровне.