Участник:Смирнова Александра/Нахождение собственных чисел квадратной матрицы методом QR разложения (3)

Эта работа прошла предварительную проверку Дата последней правки страницы: 13.11.2016 Данная работа соответствует формальным критериям. Проверено VadimVV.

Нахождение собственных чисел квадратной матрицы методом QR разложения
Последовательный алгоритм
Последовательная сложность	[math]N*O(n^3)[/math]
Объём входных данных	[math] n^2 [/math]
Объём выходных данных	[math] n [/math]
Параллельный алгоритм
Высота ярусно-параллельной формы	[math]N*O(n)[/math]
Ширина ярусно-параллельной формы	[math]O(n^2)[/math]

Основные авторы описания:

• Смирнова А.С. - описание теоретической части
• Киямова А. - описание программистской части

Содержательно все пункты обсуждались авторами вместе, и их вклад был равным.

---

Задача нахождения собственных значений и собственных векторов для матрицы [math]A[/math] заключается в поиске таких чисел [math]\lambda[/math], которые удовлетворяют уравнению:

[math]Ax=\lambda x[/math], при этом, числа [math]\lambda[/math] называются собственными значениями, а вектора [math]x[/math] - собственными векторами.

Данная задача является одной из важнейших задач линейной алгебры. Собственные вектора и собственные значения применяются в различных областях науки: в аналитической геометрии, при решении систем интегральных уравнений, в математической физике. Однако не существует простых алгоритмов прямого вычисления собственных значений для матриц в общем случае, поэтому данная задача на практике решается численными методами. Одним из таких методов является QR-алгоритм.

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

---

QR-алгоритм — это численный метод в линейной алгебре, предназначенный для решения полной проблемы собственных значений, то есть отыскания всех собственных чисел матрицы. При этом алгоритм позволяет найти и собственные вектора матрицы. Он был разработан в конце 1950-х годов независимо В. Н. Кублановской(Россия) и Дж. Фрэнсисом(Англия). Открытию QR-алгоритма предшествовал LR-алгоритм, который использовал LU-разложение вместо QR-разложения. В настоящее время LR-алгоритм используется очень редко ввиду своей меньшей эффективности, однако он был важным шагом на пути к открытию QR-алгоритма.

Суть базового QR-алгоритма заключается в итерационном приведении матрицы [math]A[/math] к некоторой подобной ей матрице [math]A_N[/math] при помощи QR-разложения. Матрица [math]A_N[/math] является правой верхней треугольной матрицей, а значит ее диагональ содержит собственные значения. В силу подобия матриц [math]A[/math] и [math]A_N[/math] их наборы собственных значений совпадают. Таким образом задача поиска собственных значений матрицы [math]A[/math] сводится к задаче выведения матрицы [math]A_N[/math] и поиска собственных значений для нее, что является тривиальной задачей.

Однако базовый QR-алгоритм может обладать очень низкой скоростью сходимости, поэтому существует несколько способов ускорить его:

• Перед итерациями привести матрицу [math]A[/math] к подобной ей матрице [math]A_H[/math], которая будет иметь форму Хессенберга. Данный шаг позволит ускорить процесс QR-разложения.
• Использовать QR-алгоритм со сдвигами. Это позволит уменьшить количество итераций алгоритма.

В дальнейшем, в данной статье под модифицированным алгоритмом будет пониматься алгоритм, использующий сдвиги и матрицу с формой Хессенберга. Под базовым алгоритмом будет пониматься алгоритм, не использующий данные приемы.

1.2 Математическое описание алгоритма

---

1.2.1 QR-разложение матрицы

Основой алгоритма является тот факт, что любую вещественную матрицу можно разложить на произведение двух матриц следующего вида:

[math]A=QR[/math], где [math]Q[/math] - ортогональная матрица ([math]Q^T=Q^{-1}[/math]), [math]R[/math] - верхняя треугольная матрица.

Данное разложение называется QR-разложением.

Есть несколько алгоритмов вычисления QR-разложения матрицы . Кратко опишем их в данной статье.

1.2.1.1 Метод Хаусхолдера (отражений) QR-разложения квадратной матрицы

Основная статья: Метод Хаусхолдера (отражений) QR-разложения квадратной матрицы

Суть метода Хаусхолдера заключается в последовательном приведении матрицы [math]A[/math] к верхней треугольной форме при помощи домножения ее на так называемые матрицы отражения. Получившаяся треугольная матрица будет искомой матрицей [math]R[/math], а матрица [math]Q[/math] будет равна произведению сопряженных матриц отражения.

На [math]i[/math]-ом шаге задача [math]i[/math]-ой матрицы отражения заключается в обнулении всех поддиагональных элементов [math]i[/math]-го столбца матрицы [math]A[/math] (при этом столбцы левее [math]i[/math]-го не изменяются). Таким образом, алгоритм состоит из [math]n[/math] шагов, на каждом из которых вычисляется очередная матрица отражения, после чего найденное отражение применяется к матрице, которая является результатом предыдущего шага.

Матрица отражения имеет вид [math]E-\frac{1}{\gamma }vv^*[/math], где вектор [math]v[/math] вычисляется из текущего [math]i[/math]-го столбца матрицы при помощи использования операции скалярного произведения векторов. Данное представление матриц отражения позволяет хранить их в виде одного вектора и сводит домножение матрицы отражения на текущую матрицу к арифметическим операциям над векторами (скалярное произведение и сложение векторов).

1.2.1.2 Метод Гивенса (вращений) QR-разложения квадратной матрицы

Основная статья: Метод Гивенса (вращений) QR-разложения квадратной матрицы

Суть метода Гивенса заключается в последовательном приведении матрицы [math]A[/math] к верхней треугольной форме при помощи домножения ее на так называемые матрицы вращения. Получившаяся треугольная матрица будет искомой матрицей [math]R[/math], а матрица [math]Q[/math] будет равна произведению сопряженных матриц вращения.

На каждом шаге задачей матрицы вращения является обнуление одного поддиагонального элемента. Вначале обнуляются все поддиагональные элементы 1-го столбца, затем 2-го и так далее до [math](n-1)[/math]-го. Таким образом, алгоритм состоит из [math]\frac{n(n-1)}{2}[/math] шагов на каждом из которых вычисляется очередная матрица вращения, после чего она применяется к матрице, которая является результатом предыдущего шага.

Матрицы вращения [math]T_{ij}[/math] по ствоей структуре очень близки к единичным матрицам, за исключением четырех элементов: элементы с номерами [math]ii[/math] и [math]jj[/math] содержат некоторое число-параметр [math]c[/math], элементы с номерами [math]ij[/math] и [math]ji[/math] содержат числа-параметры [math]-s[/math] и [math]s[/math] соответственно. Вычисление параметров [math]c[/math] и [math]s[/math] происходит на каждом шаге в зависимости от текущей матрицы и состоит из простых численных арифметических операций. Умножение матрицы вращения на текущую матрицу может быть представлено как последовательное изменение элементов с номерами [math]ik[/math] и [math]kk[/math] для всех столбцов [math]k[/math] находящихся правее столбца [math]i[/math]. Каждое такое изменение по своей структуре эквивалентно операции перемножения двух комплексных чисел.

1.2.2 QR-алгоритм нахождения собственных чисел

Пусть матрица [math]A[/math] - матрица, для которой мы хотим найти собственные значения. Тогда итерационный процесс строится следующим образом:

1. [math]A_0=A[/math].
2. Пусть имеется матрица [math]A_k[/math], тогда матрица [math]A_{k+1}[/math] строится следующим образом:

• Строится QR-разложение: [math]A_k=Q_kR_k[/math].
• Вычисляется [math]A_{k+1}=R_kQ_k[/math].

Заметим, что [math]A_{k+1}=R_kQ_k={Q_{k}^{-1}}Q_kR_kQ_k={Q_{k}^{-1}}A_kQ_k={Q_{k}^{T}}A_kQ_k[/math].

Таким образом матрицы [math]A_{k+1}[/math] и [math]A_{k}[/math] подобны для [math]\forall k[/math], а значит, в силу транзитивности подобия, все матрицы [math]A_{k}[/math] подобны матрице [math]A[/math] и имеют одинаковый набор собственных значений.

1.2.3 Сходимость алгоритма

Предположим, что для [math]\forall m[/math] выполнены следующие условия:

1. [math]A=X\Lambda X^{-1}[/math], где [math]\Lambda =\begin{bmatrix} \Lambda_1 & 0\\ 0 & \Lambda_2 \end{bmatrix}, \Lambda_1\in\mathbb{C}^{m\times m},\Lambda_2\in\mathbb{C}^{r\times r} [/math].

2. [math]\left | \lambda_1 \right | \geq ...\geq \left | \lambda_m \right | \gt \left | \lambda_{m+1} \right | \geq ...\geq \left | \lambda_{m+r} \right | \gt 0 [/math], где [math]\{\lambda_1,...,\lambda_m\} = \lambda(\Lambda_1), \{\lambda_{m+1},...,\lambda_{m+r}\} = \lambda(\Lambda_2) [/math].

3. Ведущая подматрица порядка [math]m[/math] в [math]X^{-1}[/math] невырождена.

Тогда при [math] k \rightarrow \infty [/math] последовательность матриц [math]A_k[/math] сходится к матрице с верхней треугольной формой.

Таким образом, на практике необходимо выполнять итерации до тех пор пока матрица [math]A_k[/math] не станет треугольной (также можно продолжать выполнять их пока искомая матрица не будет найдена с некоторой заранее заданной точностью [math]\varepsilon[/math]). Если итерации закончились на шаге [math]N[/math], то числа на диагонали матрицы [math]A_N[/math] будут считаться собственными значениями матрицы [math]A[/math].

1.2.4 Вещественный вариант QR-алгоритма

Если вещественная матрица [math]A[/math] имеет различные вещественные собственные значения, то, как было описано ранее, QR-алгоритм сходится к матрице с верхней треугольной формой, на диагонали которой находятся собственные значения. Однако вещественная матрица может иметь комплексные собственные значения. В данном случае алгоритм будет сходиться не к верхней треугольной матрице, а к блочной верхней треугольной матрице, которая на диагонали содержит блоки 1-го и 2-го порядка. Блоки 1-го порядка содержат различные вещественные собственные значения, блоки 2-го порядка соответствуют парам комплексных сопряженных собственных значений.

[math]A_N= \begin{bmatrix} \blacksquare& \bullet& \bullet& \cdots& \cdots& \cdots& \cdots& \cdots& \bullet\\ 0& \blacksquare& \blacksquare& \bullet& \ddots& \ddots& \ddots& \ddots& \vdots\\ 0& \blacksquare& \blacksquare& \bullet& \bullet& \ddots& \ddots& \ddots& \vdots\\ \vdots& 0& 0& \blacksquare& \bullet& \bullet& \ddots& \ddots& \vdots\\ \vdots& \ddots& 0& 0& \blacksquare& \bullet& \bullet& \ddots& \vdots\\ \vdots& \ddots& \ddots& 0& 0& \blacksquare& \blacksquare& \ddots& \vdots\\ \vdots& \ddots& \ddots& \ddots& 0& \blacksquare& \blacksquare& \ddots& \bullet\\ \vdots& \ddots& \ddots& \ddots& \ddots& \ddots& \ddots& \ddots& \bullet\\ 0& \cdots& \cdots& \cdots& \cdots& \cdots& 0& 0& \blacksquare \end{bmatrix}[/math].

В дальнейшем, в данной статье, матрицы, имеющие вышеописанную форму, будут называться квазитреугольными.

1.2.5 Приведение матрицы к форме Хессенберга

Матрицей, имеющей форму Хессенберга, называется такая матрица, у которой все элементы, находящиеся ниже первой поддиагонали, равны нулю ([math]a_{ij}=0[/math] при [math]i\lt j+1[/math]). Пример такой матрицы приведен ниже:

[math]\begin{bmatrix} 1& 2& 3& 4\\ 2& 5& 6& 7\\ 0& 3& 8& 9\\ 0& 0& 4& 1 \end{bmatrix}[/math]

Любую матрицу [math]A[/math] можно привести к подобной ей матрице [math]A_H[/math], имеющей форму Хессенберга (в силу подобия данные матрицы будут иметь одинаковые собственные значения). Наличие нулевых элементов в данной матрице позволяет ускорить процесс QR-разложения, причем данное ускорение будет иметь место на каждой итерации алгоритма, т.к. матрица с формой Хессенберга инвариантна относительно QR-итерации. Ускорение можно получить за счет использования модифицированного метода Гивенса(вращений) QR-разложения, который из-за изначального наличия нулевых элементов будет состоять не из [math]\frac{n(n-1)}{2}[/math] шагов, а из [math]n-1[/math] шагов (будет происходить домножение только на те матрицы вращения [math]T_{ij}[/math], у которых [math]i=j+1[/math]).

Одним из способов приведения матрицы к форме Хессенберга является преобразование Хаусхолдера. Данный алгоритм состоит из [math]n-1[/math] итераций. Пусть имеется матрица [math]A^{(k)}[/math], тогда для перехода к матрице [math]A^{(k+1)}[/math] проделывается следующее:

• Вычисление параметра [math]\alpha[/math]: [math]\alpha=-sgn(a_{k+1,k}^{(k)})\sqrt{\sum_{j=k+1}^{n}(a_{j,k}^{(k)})^2}[/math]

• Вычисление параметра [math]r[/math]: [math]r=\sqrt{\frac{1}{2}(\alpha^2-a_{k+1,k}^{(k)}\alpha )}[/math]

• Вычисление вектора [math]v^{(k)}=\begin{bmatrix}v_1\\ v_2\\ \vdots \\ v_n\end{bmatrix}[/math], где [math]v_{1}^{(k)}=v_{2}^{(k)}=...=v_{k}^{(k)}=0, v_{k+1}^{(k)}=\frac{a_{k+1,k}^{(k)}-\alpha}{2r}[/math], а остальные элементы [math]v_{j}^{(k)}=\frac{a_{jk}^{(k)}}{2r}[/math].

• Вычисление матрицы [math]P^{(k)}[/math]: [math]P^{(k)}=E-2v^{(k)}(v^{(k)})^T[/math]

• Вычисление матрицы [math]A^{(k+1)}[/math]: [math]A^{(k+1)}=P^{(k)}A^{(k)}(P^{(k)})^T[/math]. Важно отметить, что форма, которой обладают матрицы [math]P^{(k)}[/math], позволяет свести данную операцию перемножения матриц к менее затратным операциям перемножения матрицы на вектор.

1.2.6 QR-алгоритм со сдвигами

QR-алгоритм со сдвигами позволяет сократить количество итераций, необходимых для сходимости. Пусть у нас есть матрица [math]A_k[/math], тогда процесс перехода к матрице [math]A_{k+1}[/math] выглядит следующим образом:

• На каждом шаге подбирается число [math]\nu_k[/math] и ищется следующее QR-разложение: [math]A_k-\nu_kE=Q_kR_k[/math].
• Вычисляется матрица [math]A_{k+1}[/math]: [math]A_{k+1} = R_kQ_k+\nu_kE[/math].

При этом сохраняется свойство подобия матриц [math]A_k[/math] и [math]A_{k+1}[/math]:

[math]A_{k+1} = R_kQ_k+\nu_kE=Q_{k}^{T}Q_kR_kQ_k+\nu_kE=Q_{k}^{T}(A_k-\nu_kE)Q_k+\nu_kE=Q_{k}^{T}A_kQ_k-Q_{k}^{T}(\nu_kE)Q_k+\nu_kE=Q_{k}^{T}A_kQ_k-\nu_kE+\nu_kE=Q_{k}^{T}A_kQ_k[/math].

1.2.6.1 Подбор параметра [math]\nu_k[/math]

//TODO

1.3 Вычислительное ядро алгоритма

---

1.3.1 Базовый алгоритм

QR-алгоритм обладает двумя вычислительными ядрами, которые повторяются на каждой итерации:

1. Вычисление QR-разложения матрицы: [math]A_k=Q_kR_k[/math]. Существует несколько методов решения данной задачи:
   • Метод Хаусхолдера (отражений): вычислительное ядро данного алгоритма состоит из операций скалярного произведения, необходимых для вычисления матрицы отражения, и из операций скалярного произведения, необходимых для пересчета матрицы на каждом шаге.
   • Метод Гивенса (вращений): вычислительное ядро данного алгоритма состоит из численных арифметических операций, необходимых для вычисления параметров матрицы вращения, и из операций (эквивалентных перемножению комплексных чисел), необходимых для пересчета матрицы на каждом шаге.
2. Перемножение двух плотных матриц: [math]A_{k+1}=R_kQ_k[/math].

1.3.2 Модифицированный алгоритм

Модифицированный QR-алгоритм обладает тремя вычислительными ядрами, первое вычисляется единожды, второе и третье повторяются на каждой итерации:

1. Приведение изначальной матрицы к форме Хессенберга: вычислительным ядром данного алгоритма является подсчет матрицы [math]A^{(k+1)}=P^{(k)}A^{(k)}(P^{(k)})^T[/math].
2. Вычисление QR-разложения матрицы: [math]A_k-\nu_kE=Q_kR_k[/math] при помощи модифицированного метода Гивенса (вращений). Описание вычислительного ядра не отличается от приведенного в описании базового алгоритма, единственная разница заключается в значительно меньшем количестве матриц вращения.
3. Перемножение двух плотных матриц: [math]A_{k+1}-\nu_kE=R_kQ_k[/math].

1.4 Макроструктура алгоритма

---

Как уже было описано ранее, базовый QR-алгоритм содержит в себе две макрооперации:

1. Вычисление QR-разложения матрицы: [math]A_k=Q_kR_k[/math].
2. Перемножение двух плотных матриц: [math]A_{k+1}=R_kQ_k[/math].

В случае модифицированного QR-алгоритма появляется еще макрооперация приведения матрицы к форме Хессенберга.

1.5 Схема реализации последовательного алгоритма

---

1.5.1 Базовый алгоритм

Опишем необходимый для реализации цикл при помощи псевдокода:

A - исходная матрица.
curA - текущая матрица, на основе которой будет вычисляться QR-разложение на каждом шаге.
nextA - новая матрица, полученная после перемножения матриц R и Q.
triangular - функция, проверяющая, имеет ли матрица квазитреугольную форму.
difference - функция, проверяющая, что элементы двух матриц, стоящие на одинаковых местах, различаются не более чем на eps (данная функция нужна чтобы проверять не только сходимость матрицы к квазитреугольной форме, но и сходимость ее ненулевых элементов).

curA = A
nextA = A
while ( not (triangular(nextA) & difference(curA,nextA,eps)) )
{
    curA = nextA
    findQRdecomposition(curA,Q,R)
    nextA = R*Q
}

1.5.2 Модифицированный алгоритм

A - исходная матрица.
curA - текущая матрица, на основе которой будет совершаться сдвиг и вычисляться QR-разложение на каждом шаге.
nextA - новая матрица, полученная после перемножения матриц R и Q.
nu - параметр сдвига
shiftA - текущая матрица со сдвигом.
triangular - функция, проверяющая, имеет ли матрица квазитреугольную форму.
difference - функция, проверяющая, что элементы двух матриц, стоящие на одинаковых местах, различаются не более чем на eps (данная функция нужна чтобы проверять не только сходимость матрицы к квазитреугольной форме, но и сходимость ее ненулевых элементов).

curA = A
nextA = A
while ( not (triangular(nextA) & difference(curA,nextA,eps)) )
{
    curA = nextA
    nu = computeNu(curA)
    shiftA = curA - nu*E
    findQRdecomposition(shiftA,Q,R)
    nextA = R*Q + nu*E
}

1.6 Последовательная сложность алгоритма

---

Подсчитаем сложность одной итерации QR-алгоритма (расчет сложностей для QR-разложения и перемножения матриц представлен в статьях, посвященных данным алгоритмам).

1. QR-разложение матрицы.
   • Метод Хаусхолдера (отражений) имеет сложность [math]\frac{4}{3}n^3[/math].
   • Метод Гивенса (вращений) имеет сложность [math]2n^3[/math].
2. Перемножение двух плотных матриц имеет сложность [math]n^3[/math].
3. Проверка матрицы на квазитреугольную форму состоит из набора сравнений элементов с номерами [math]ij[/math] ([math]i\gt j+1[/math]) с нулем (таких элементов [math]\frac{(n-2)(n-1)}{2}[/math]). Поддиагональные элементы с номерами [math]ij[/math] ([math]i=j+1[/math]) должны быть проверены на соответствие необходимой квазитреугольной форме. Для этого достаточно для каждого такого элемента проверить следующее условие: [math]a_{i+1,i}==0 \vee a_{i,i-1}==0 \wedge a_{i+2,i+1}==0[/math] (либо поддиагональный элемент равен 0, либо, в противном случае, соседние поддиагональные элементы равны 0, чтобы текущий элемент соответствовал блоку 2-го порядка). Таких проверок поддиагональных элементов будет [math]n-1[/math]. После данных проверок следует набор логических операций "И" между результатами всех сравнений (таких операций будет [math]\frac{n(n-1)}{2}-1[/math]).
4. Сравнение новой матрицы с предыдущей состоит из операций вычитания и сравнения для каждой пары ненулевых соответствующих элементов (такие пары имеют номера элементов [math]ij[/math] ([math]i \geq j+1[/math]), количество таких пар равно [math]\frac{n(n+1)}{2}+(n-1)[/math]), а также из набора логических операций "И" между результатами сравнений (таких операций будет [math]\frac{n(n+1)}{2}+(n-1)-1[/math]).

Итого, в сумме получаем [math]O(n^3)[/math] - сложность алгоритма на каждой итерации. Если алгоритм остановился на итерации с номером [math]N[/math], то общая сложность алгоритма будет равна [math]N*O(n^3)[/math].

1.7 Информационный граф

---

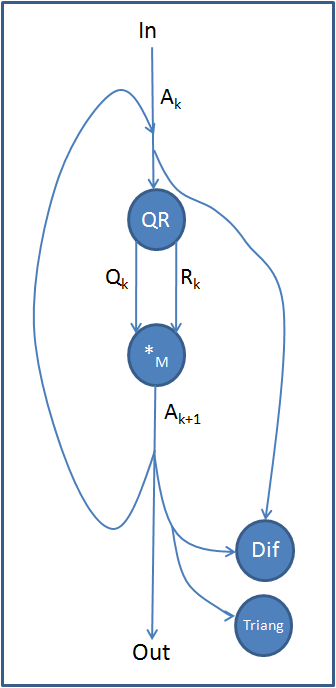
На рисунке 1 изображен информационный граф QR-алгоритма. Вершины данного графа обозначают следующее:

• QR - операция QR-разложения матрицы.
• *_M - операция перемножения матриц.
• Triang - операция проверки матрицы на квазитреугольную форму.
• Dif - операция проверки различия элементов двух матриц не более чем на некоторое заданное число.

Рисунок 1. Информационный граф QR-алгоритма

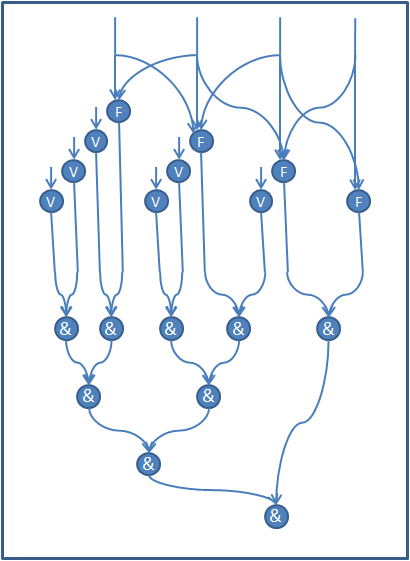
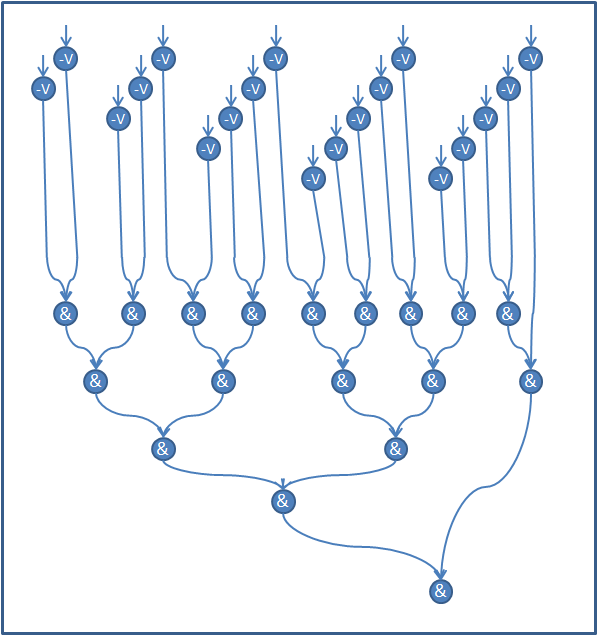
Подробные графы операций QR-разложения (Метод Хаусхолдера (отражений), Метод Гивенса (вращений)) и перемножения матриц можно найти в статьях, посвященных этим алгоритмам. Далее рассмотрим информационные графы операций Triang (рис.2) и Dif (рис.3) на примере матрицы размера [math]5 \times 5[/math]. Графы для других матриц выглядят аналогичным образом.

Рисунок 2. Информационный граф операции Triang, которая проверяет соответствие квазитреугольной форме

Вершины V соответствуют операции сравнения с 0. Вершины F соответствуют проверке поддиагональных элементов на соответствие квазитреугольной форме, которая была описана в предыдущем разделе. Вершины & соответствуют логической операции "И".

Рисунок 3. Информационный граф операции Dif, которая проверяет сходимость ненулевых элементов

Вершины -V соответствуют операции вычитания и сравнения с 0. Вершины & соответствуют логической операции "И".

1.8 Ресурс параллелизма алгоритма

---

На макроуровне (который можно увидеть на информационном графе QR-алгоритма) алгоритм не обладает ресурсами параллелизма. Все макрооперации внутри итерации, а также сами итерации выполняются последовательно (за исключением операций Triag и Dif, которые могут выполняться параллельно). Основной ресурс параллелизма заложен отдельно в каждой из макроопераций. На каждой итерации алгоритм имеет следующие параллельные характеристики:

1. QR-разложение матрицы (описание ресурсов параллелизма для алгоритмов QR-разложения можно найти в статьях, посвященных этим алгоритмам).
   • Метод Хаусхолдера (отражений) имеет высоту ярусно-параллельной формы [math]O(n^2)[/math] и ширину ярусно-параллельной формы [math]O(n)[/math].
   • Метод Гивенса (вращений) имеет высоту ярусно-параллельной формы [math]11n-16[/math] и ширину ярусно-параллельной формы [math]O(n^2)[/math].
2. Перемножение двух плотных матриц имеет высоту ярусно-параллельной формы [math]n[/math] и ширину ярусно-параллельной формы [math]n^2[/math].
3. Проверка матрицы на выходе из итерации.
   • Проверка матрицы на квазитреугольную форму состоит из одного яруса сравнений для каждого элемента и последующих ярусов, вычисляющих итоговый результат при помощи логической операции "И". Для вычисления итогового результата можно использовать метод сдваивания, который дает высоту ярусно-параллельной формы порядка логарифма от количества элементов, над которыми совершается операция. Таким образов высота ярусно-параллельной формы будет равна [math]O(log_2n)[/math]. Ширина ярусно-параллельной формы достигается на ярусе сравнений для каждого элемента и равна [math]O(n^2)[/math].
   • Сравнение новой матрицы с предыдущей состоит из одного яруса сравнений для каждого элемента и последующих ярусов, вычисляющих итоговый результат при помощи логической операции "И". Высота ярусно-параллельной формы будет равна [math]O(log_2n)[/math]. Ширина ярусно-параллельной формы достигается на ярусе сравнений для каждого элемента и равна [math]O(n^2)[/math].

Таким образом, основной вклад в высоту ярусно-параллельной формы одной итерации вносит операция QR-разложения матрицы и она будет равна [math]O(n)[/math], если использовать метод Гивенса. Ширина ярусно-параллельной формы будет равна [math]O(n^2)[/math]. Если алгоритм остановился на итерации с номером [math]N[/math], то параллельные характеристики для всего алгоритма будут равны [math]N*O(n)[/math] для высоты и [math]O(n^2)[/math] для ширины ярусно-параллельной формы.

1.9 Входные и выходные данные алгоритма

---

Входные данные:

квадратная вещественная плотная матрица [math]A[/math]: [math]A \in \R^{n \times n}[/math].

Объем входных данных:

[math]n^2[/math] (необходимо хранить все элементы матрицы).

Выходные данные:

собственные значения матрицы [math]A[/math].

Объем выходных данных:

[math]n[/math] (квадратная матрица размера [math]n \times n[/math] имеет ровно [math]n[/math] собственных значений при этом некоторые из них могут быть комплексными).

1.10 Свойства алгоритма

---

• Cоотношение последовательной и параллельной сложности алгоритма квадратично, что дает довольно большой выигрыш.
• Вычислительная мощность, которая показывает, сколько операций приходится на единицу переданных данных, равна [math]\frac{N*O(n^3)}{n^2+n}=N*O(n)[/math], а значит перемещение данных для их обработки не будет составлять большой проблемы.
• Алгоритм является недетерминированным, т.к. заранее неизвестно сколько итераций необходимо совершить до момента сходимости.
• Скорость сходимости алгоритма зависит от собственных значений. Чем ближе по модулю соседние собственные значения, тем меньше скорость сходимости. Этот недостаток призван решить QR-алгоритм со сдвигами.

2 Программная реализация алгоритма

---

---

---

---

---

---

2.7 Существующие реализации алгоритма

---

2.7.1 Последовательные реализации

1. LAPACK (Linear Algebra PACKage) — библиотека с открытым исходным кодом, содержащая методы для решения основных задач линейной алгебры. Написана на языке Fortran с использованием библиотеки BLAS и является развитием пакета LINPACK. Находится в открытом доступе в соответствии с модифицированной лицензией BSD, в том числе и для коммерческого использования.
   • Полный алгоритм нахождения собственных значений: функция dhseqr.
   • QR-разложение: функция dgeqrf.
   • Перемножение матриц: функция dgemm.
2. ALGLIB - это кросс-платформенная библиотека численного анализа, поддерживающая несколько языков программирования (C++, C#, Pascal, VBA) и несколько операционных систем (Windows, Linux, Solaris). ALGLIB является свободным программным обеспечением, которое использует двойное лицензирование: оно может быть использовано в соответствии с лицензией GPL (версии 2+), а для использования в коммерческих целях необходимо купить отдельную лицензию.
   • Полный алгоритм нахождения собственных значений: подпрограмма RMatrixEVD.
   • QR-разложение: подпрограмма rmatrixqr реализует QR-разложение для вещественных матриц, cmatrixqr – для комплексных матриц.
   • Перемножение матриц: для перемножения матриц ALGLIB использует соответствующую реализацию библиотеки BLAS.
3. Eigen – библиотека шаблонов для линейной алгебры, написанная на языке C++. Eigen – свободно распространяемое программное обеспечение. Начиная с версии 3.1.1, оно лицензируется MPL2, на ранние версии распространяется действие лицензии LGPL3+.
   • Полный алгоритм нахождения собственных значений: модуль Eigenvalues module.
   • QR-разложение: модуль QR module.
   • Перемножение матриц: операторы * и *=.

2.7.2 Параллельные реализации

1. ScaLAPACK (Scalable Linear Algebra PACKage) — библиотека с открытым исходным кодом, включающая в себя подмножество процедур LAPACK, переработанных для использования на MPP-компьютерах. ScaLAPACK разработана с использованием PBLAS и BLACS, и предназначена для вычислений на любом компьютере или кластере поддерживающим MPI или PVM. Библиотека в настоящее время написана на языке Fortran. Находится в открытом доступе в соответствии с модифицированной лицензией BSD, в том числе и для коммерческого использования.
   • Полный алгоритм нахождения собственных значений: функция pdhseqr.
   • QR-разложение: функция pdgeqrf.
   • Перемножение матриц: функция pdgemm.
2. PLAPACK (Parallel Linear Algebra Package) — пакет функций LAPACK для параллельного решения задач линейной алгебры. Пакет функций PLAPACK является альтернативой библиотеке ScaLAPACK. Для осуществления межпроцессорных коммуникаций в PLAPACK использован интерфейс передачи сообщений MPI. При передаче сообщений в PLAPACK в основном используются коллективные операции, такие, как обобщенная передача данных от одного процесса всем процессам (MPI_Scatter), обобщенная передача данных от всех процессов одному процессу (MPI_Gather), широковещательная рассылка (MPI_Bcast) и другие. PLAPACK включает интерфейсы для языков Fortran и С.
   • QR-разложение: функция PLA_QR.
   • Перемножение матриц: функция PLA_Gemm.