Участник:Elijah/Нахождение собственных чисел квадратной матрицы методом QR разложения

Эта работа ждет рассмотрения преподавателем Дата последней правки страницы: 01.11.2016 Авторы этой статьи считают, что задание выполнено.

Нахождение собственных чисел квадратной матрицы методом QR разложения
Последовательный алгоритм
Последовательная сложность	[math]N * O(n^3)[/math]
Объём входных данных	[math]n^2[/math]
Объём выходных данных	[math]n[/math]
Параллельный алгоритм
Высота ярусно-параллельной формы	[math] N * (12n - 15) [/math]
Ширина ярусно-параллельной формы	[math] O(n^2) [/math]

Основные авторы описания:
И.В.Афанасьев, разделы 1.3 - 1.10 (базовый алгоритм), 2.1, 2.3, 2.4, 2.7

В.А.Шишватов, разделы 1.1, 1.2, 1.3 - 1.10 ((алгоритм с преобразованием к матрице Хессенберга)

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

QR-алгоритм — это численный метод в линейной алгебре, предназначенный для решения полной проблемы собственных значений, то есть отыскания всех собственных чисел и собственных векторов матрицы. Был разработан в конце 1950-х годов независимо В. Н. Кублановской и Дж. Фрэнсисом. [1]

Данный алгоритм хорошо подходит для поиска собственных значений матриц общего вида, порядок которых составляет порядке тысячи.

Суть алгоритма состоит в итеративном приведении матрицы A к верхнетреугольном виду с помощью последовательных QR разложений и матричный умножений. Данные матрицы на каждой итерации подобны между собой, так как данные умножения равносильны ортогональным преобразованиям. В следствии подобия, собственные значения этих матриц равны между собой.

1.2 Математическое описание алгоритма

1.2.1 QR-алгоритм нахождения собственных чисел

Пусть [math]A[/math] — вещественная матрица, для которой мы хотим найти собственные числа. Положим [math]A_0 = A[/math]. На [math]k[/math]-ом шаге (начиная с [math]k = 0[/math]) вычислим QR-разложение [math]A_k = Q_k R_k[/math], где [math]Q_k[/math] — ортогональная матрица (то есть [math]Q_k^\text{T} = Q_k^{-1}[/math]), а [math]R_k[/math] — верхняя треугольная матрица. Затем мы определяем [math]A_{k+1} = R_k Q_k[/math].

Заметим, что

[math] A_{k+1} = R_k Q_k = Q_k^{-1} Q_k R_k Q_k = Q_k^{-1} A_k Q_k = Q_k^{T} A_k Q_k, [/math]

то есть все матрицы [math]A_k[/math] являются подобными, то есть их собственные значения равны.

Пусть все диагональные миноры матрицы [math]A[/math] вырождены. Тогда последовательность матриц [math]A[/math] при [math] k \rightarrow \infty[/math] сходится по форме к клеточному правому треугольному виду, соответствующему клеткам с одинаковыми по модулю собственными значениями.

1.2.2 Сходимость QR-алгоритма нахождения собственных чисел

Сходимость QR-алгоритма определяется как сходимость поддиагональной подматрицы матрицы [math]A_k[/math] ([math]A_k = R_{k-1}Q_{k-1}[/math]) к нулевой матрице.

Предположим, что для матрицы [math]A \in \mathbb{C}^{n \times n}[/math] выполнены следующие условия:

1. [math]A = X \Lambda X^{-1}, \quad \Lambda = \begin{bmatrix} \Lambda_1 & 0 \\ 0 & \Lambda_2 \end{bmatrix}, \quad \Lambda_1 \in \mathbb{C}^{m \times m}, \quad \Lambda_2 \in \mathbb{C}^{r \times r}[/math];
2. [math]\left | \lambda_1 \right | \ge \ldots \ge \left | \lambda_m \right | \gt \left | \lambda_{m+1} \right | \ge \ldots \ge \left | \lambda_{m+r} \right | \gt 0, \quad \{ \lambda_1, \ldots, \lambda_m \} = \lambda(\Lambda_1), \quad \{ \lambda_{m+1}, \ldots, \lambda_{m+r} \} = \lambda(\Lambda_2)[/math];
3. ведущая подматрица порядка [math]m[/math] в [math]X^{-1}[/math] невырожденная.

Пусть QR-алгоритм порождает последовательность матриц вида:

[math]A_k = \begin{bmatrix} A_{11}^{(k)} & A_{12}^{(k)} \\ A_{21}^{(k)} & A_{22}^{(k)} \end{bmatrix}[/math].

Тогда [math]A_{21}^{(k)} \rightarrow O[/math] при [math] k \rightarrow \infty[/math]. При достижении необходимой точности матрицу [math]A_{21}^{(k)}[/math] можно заменит нулевой матрицей. В таком случае собственные значения необходимо искать для матриц [math]A_{11}^{(k)}[/math] и [math]A_{22}^{(k)}[/math].

Если условия 1-3 выполнены для всех [math]m \in \{1, ..., n-1\}[/math], то все поддиагональные матрицы сходятся к нулевым матрицам. Таким образом, все элементы, лежащие ниже главной диагонали стремятся к нулю, и диагональные элементы матриц [math]A_k[/math] сходятся к искомым собственным значениям матрицы [math]A[/math]

1.2.3 Приведение матрицы к матрице Хессенберга

Для преобразования матрицы к матрице Хессенберга используется преобразование Хаусхолдера.

Для каждого [math] k = 1,2,... n-1 [/math]

[math] \displaystyle \alpha = -\operatorname{sgn}(a^k_{k+1,k})\sqrt{\sum_{j=k+1}^{n}(a^k_{jk})^2} [/math];

[math] r = \sqrt{\frac{1}{2}(\alpha^{2}-a^k_{k+1,k}\alpha)} [/math];

[math]v^k_1 = v^{k}_2 = \cdots = v^k_k=0;[/math]

[math] v^{k}_{k+1} = \frac{a^{k}_{k+1,k}-\alpha}{2r}[/math]

[math] v^{k}_j = \frac{a^{k}_{jk}}{2r}[/math], для [math]j = k+2; k+3, ..., n[/math]

[math] \displaystyle P^{k} = I - 2v^{(k)}(v^{(k)})^\text{T}[/math]

[math]\displaystyle A^{(k+1)} = P^{k}A^{(k)}(P^{k})^\text{T}[/math]

При этом матрица [math]P[/math] не вычисляется и используется напрямую. Вместо этого используются следующие вычисления

[math]\displaystyle B^{(k)} = P^{k}A^{(k)} = (I - 2v^{(k)}(v^{(k)})^\text{T}) A^{(k+1)} = A^{(k+1)} - 2A^{(k+1)}v^{(k)}(v^{(k)})^\text{T}[/math]

[math]\displaystyle A^{(k+1)} = P^{k}A^{(k)}(P^{k})^\text{T} = B^{(k)}(P^{k})^\text{T} = ((B^{(k)})^\text{T})^\text{T}(P^{k})^\text{T} = (P^{k}(B^{(k)})^\text{T})^\text{T} = ((B^{(k)})^\text{T} - 2B^{(k)}v^{(k)}(v^{(k)})^\text{T})^\text{T}[/math]

Таким образом перемножение матриц [math]P^{k}A^{(k)}[/math] и [math]B^{k}P^{(k)}[/math] имеет сложность [math]O(n^2) [/math](умножения матрицы на вектор) вместо [math]O(n^3)[/math] (перемножение матриц)

1.3 Вычислительное ядро алгоритма

1.3.1 Базовый алгоритм

У базового QR алгоритма есть два вычислительных ядра:

1. операция поиска QR разложения с использованием метода Гивенса
2. матричное умножение полученных матриц

Для получения [math]QR[/math]-разложения методом Гивенса [math]A[/math] матрицу приводят к правой треугольной [math]R[/math] последовательностью умножений её слева на матрицы вращения [math]T_{1 2}, T_{1 3}, ..., T_{1 n}, T_{2 3}, T_{2 4}, ..., T_{2 n}, ... , T_{n-2 n}, T_{n-1 n}[/math].

Матричное умножение может быть выполнено любым классическим способом: для плотных матриц [math]A[/math] (элементы [math]a_{ij}[/math]) и [math]B[/math] (элементы [math]b_{ij}[/math]) вычисляется плотная матрица [math]C[/math]с элементами [math]c_{ij}[/math] по формуле:

Формулы метода:

[math] \begin{align} c_{ij} = \sum_{k = 1}^{n} a_{ik} b_{kj}, \quad i \in [1, m], \quad i \in [1, l]. \end{align} [/math]

1.3.2 Алгоритм с преобразованием к матрице Хессенберга

Для QR алгоритма с использования матрицы Хессенберга:

1. получение матрицы Хессенберга из исходной матрицы
2. операция поиска QR разложения с использованием модифицированного метода Гивенса

Для преобразования исходной матрицы к матрице Хессенберга используются преобразования Хаусхолдера (см. раздел 1.2.3)

Для получения [math]QR[/math]-разложения методом Гивенса для матрицы Хессенберга [math]A[/math], матрицу приводят к правой треугольной [math]R[/math] последовательностью умножений её слева на матрицы вращения [math]T_{1 2}, T_{2 3}, T_{3 4}, ..., T_{(n-1)\ n}[/math].

Более подробное описание вычислительных ядер можно найти по соответствующим ссылкам в разделе 1.4.

1.4 Макроструктура алгоритма

Как уже описано в описании ядра алгоритма, базовая версия QR-алгоритма на каждой итерации использует следующие алгоритмы:

1. Метод Гивенса (вращений) QR-разложения квадратной матрицы или Метод Хаусхолдера(отражений) QR-разложения_квадратной_матрицы
2. Перемножение плотных неособенных матриц

В случае использования матрицы Хессенберга:

1. Получение матрицы Хессенберга из исходной матрицы с помощью преобразований Хаусхолдера.
2. Метод Гивенса (вращений) QR-разложения квадратной матрицы. При этом количество элементов матрицы, которые нужно занулять, на порядок меньше, чем в базовом варианте.

1.5 Схема реализации последовательного алгоритма

1.5.1 Базовый алгоритм

Последовательная реализация простейшего алгоритма состоит из некоторого числа итераций

Каждая итерация состоит из следующих действий (с начальным условием [math] A_0 = A[/math]):

1. Для матрицы [math] A_{n} [/math] строится QR разложение любым доступным последовательным алгоритмом на матрицы [math] Q_{n} [/math] и [math] R_{n} [/math]
   
2. Матрицы [math] R_{n} [/math] и [math] Q_{n} [/math] перемножаются, таким образом получается матрица [math] A_{n+1} = R_{n} * Q_{n} [/math] для следующей итерации [math] n + 1 [/math]
3. Проверятся, приведена ли матрица к верхнетреугольной форме, и если да, то производится выход из цикла.

1.5.2 Алгоритм с преобразованием к матрице Хессенберга

На первом этапе исходная матрица [math]A[/math] преобразуется к матрице Хессенберга [math]H[/math], которая будет иметь такие же собственные значения, что и изначальная матрица.

Затем производится некоторое число итераций, состоящих из следующих действий (с начальным условием [math] A_0 = H[/math]):

1. Для матрицы [math] A_{n} [/math] строится QR разложение с помощью метода вращения Гивенса. При этом занулять нужно не все элементы, а только [math] a_{i + 1, i} [/math], где [math]i \in {1, n - 1}[/math]. Полученная матрица будет опять являться матрицей Хессенберга.
2. Проверятся, приведена ли матрица к верхнетреугольной форме, и если да, то производится выход из цикла.

1.6 Последовательная сложность алгоритма

1.6.1 Последовательная сложность базового алгоритма

Рассчитаем последовательную сложность базового алгоритма. Пусть [math] A \in \mathbb{R}^{n \times n}[/math], и для приведения матрицы к треугольной форме необходимо произвести N итераций алгоритма.
На каждой итерации алгоритма производится QR разложение (сложностью [math] 2 * n^3 [/math]) и матричное умножение (сложностью [math] n^3 [/math]). Проверка того, имеет ли матрица треугольную форму, может быть проведена за [math] n^2 [/math] операций.
Таким образом итоговая сложность одной итерации составляет: [math] 3*n^3 + n^2 = O(n^3)[/math]
Общая сложность алгоритма при [math] N [/math] итерациях составляет [math] N * O(n^3) [/math]

1.6.2 Последовательная сложность алгоритма с приведением матрицы к матрице Хессенбрга

Данный алгоритм состоит из двух этапов:

1. преобразование исходной матрицы к матрице Хессенберга
2. QR-разложение методом Гивенса

1.6.2.1 Сложность алгоритма приведения матрицы к матрице Хессенбрга

На каждой итерации алгоритма приведения матрицы к матрице Хессенбрга требуется вычислить:

1. [math]\alpha[/math] со сложность [math]O(n)[/math]
2. [math]r[/math] со сложностью [math]O(1)[/math]
3. [math]v^k[/math] со сложностью [math]O(n)[/math]
4. [math]A^{(k+1)}[/math] со сложностью [math]O(n^2)[/math]

Таким образом вычислительная сложность одной итерации равна [math]O(n^2)[/math]. Всего таких итераций [math]n[/math], поэтому общая сложность алгоритма равна [math]O(n^3)[/math].

1.6.2.2 Сложность алгоритма QR-разложения методом Гивенса

Метод Гивенса использует матрицы вращения, чтобы занулить ненулевые элементы матрицы под главной диагональю на каждой итерации. Умножение на одну матрицу вращения имеет вычислительную сложность [math]O(n)[/math]. Для случая произвольной матрицы в худшем случае потребуется занулить [math]\frac{n^2 - n}{2}[/math] элементов. Если матрица является матрицей Хессенберга, то таких элементов будет всего лишь [math]n - 1[/math].

Таким образом, для произвольной матрицы одна итерация алгоритма QR-разложения имеет вычислительную сложность равную [math]O(n^3)[/math], для матрицы Хессенберга - [math]O(n^2)[/math]. Проверка на то, является ли матрица треугольной, имеет сложность [math]O(n^2)[/math], что не влияет на порядок сложности.

Если всего требуется [math]N[/math] итераций для преобразования матрицы к треугольному виду, то для для произвольной матрицы сложность будет [math]N * O(n^3)[/math], для матрицы Хессенберга - [math]N * O(n^2)[/math]

1.6.2.3 Итоговая сложность

Таким образом, общая вычислительная сложность алгоритма вычисления собственных значений с приведением матрицы к матрице Хессенбрга равна [math]O(n^3) + N * O(n^2)[/math]

1.7 Информационный граф

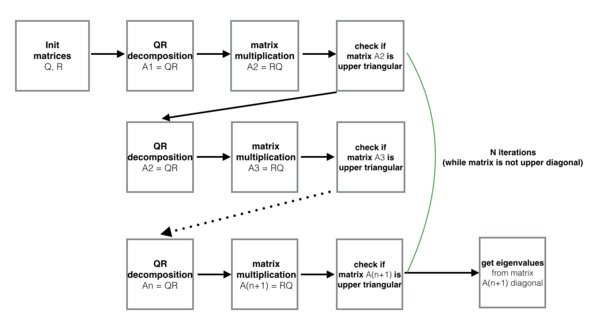
Макрограф алгоритма изображён на рисунке 1. Он представляет из себя верхний уровень алгоритма, на котором в цикле итеративно вызываются следующие операции:

1. Инициализация матриц (init matrices)
2. QR разложение (QR decomposition)
3. Матричное умножение (matrix multiplication)
4. Проверка, приведена ли матрица к верхней треугольной форме (check if matrix is upper triangular)
5. Получение собственных значений из диагонали матрицы (get eigenvalues from matrix diagonal)

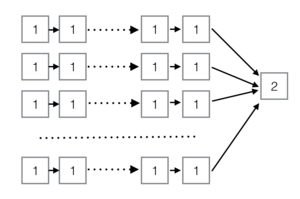
Информационные графы QR разложения и матричного умножения могут быть найдены по приведенным ссылкам. Информационный граф проверки того, приведена ли матрица к верхнетреугольной форме, будет приведен далее на рисунке 2. Информационные графы инициализации и получения собственных значений представляют собой работу с вводом и выводом входных/выходных данных, и, поэтому, рассматриваться не будут.

Рисунок 1. Информационный граф базовой версии QR-алгоритма без отображения входных и выходных данных. N итераций.

Рисунок 2. Информационный граф проверки приведенности матрицы к верхнетреугольной форме.

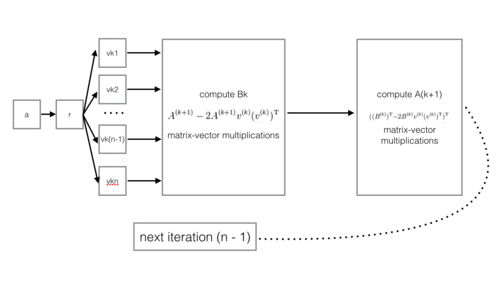
В случае оптимизации алгоритма с приведением матрицы к форме Хессенберга, инициализация матрицы (int matrices (1)), будет включать в себя преобразование хаусхолдера, имеющее следующий граф алгоритма:

Рисунок 3. Информационный граф проверки хаусхолдера.

1.8 Ресурс параллелизма алгоритма

Все итерации базового QR-алгоритма производятся последовательно, поэтому на верхнем уровне алгоритм чисто последователен.

Основной ресурс параллелизма представлен на нижнем уровне, при реализации различных операций, используемых в алгоритме, таких как QR разложение методом вращений и матричное умножение.

1.8.1 Параллельная сложность базового QR-алгоритма

Посчитаем параллельную сложность каждой операции по отдельности, а затем, по полученным данным, и всего алгоритма целиком:

1. Параллельная сложность QR разложения методом вращений составляет [math] 11n - 16 [/math]
   
2. Параллельная сложность матричного умножения составляет [math] n [/math].
   
3. Параллельная сложность проверки, является ли матрица верхнетреугольной, равна n.
   

Таким образом параллельная сложность каждой итерации составляет [math] 13n - 15 [/math]. При N итерациях, которые необходимо производить последовательно, итоговая сложность базового алгоритма составляет [math] N * (13n - 15) [/math], что в упрощенном виде равно [math] N * O(n) [/math]

1.8.2 Параллельная сложность алгоритма с приведением матрицы к форме Хессенберга:

Снова вычислим параллельную сложность каждой операции по отдельности, а затем, по полученным данным, и всего алгоритма целиком:

1. Параллельная сложность приведения матрицы к форме Хессенберга составляет [math] O(n^2) [/math]
2. Параллельная сложность каждой итерации с приведенной матрицы составляет [math] O(n) [/math]

Таким образом параллельная сложность всего алгоритма при N итерациях составляет [math] O(n^2) + N*O(n) [/math].

1.9 Входные и выходные данные алгоритма

• Входные данные: плотная квадратная матрица [math]A[/math] (элементы [math]a_{ij}[/math]).

• Объём входных данных: [math]n^2[/math].

• Выходные данные: [math]n[/math] вещественных собственных чисел [math] | l_{i} | [/math] матрицы [math]A[/math]

• Объём выходных данных: [math]n[/math].

1.10 Свойства алгоритма

Соотношение последовательной и параллельной сложности для базового является квадратичным, что даёт хороший стимул для распараллеливания. Для оптимизированного алгоритма данное соотношение линейно.

Вычислительная мощность, равная отношению числа операций [math] N * O(n^3) [/math] к суммарному объему входных и выходных данных [math] n^2 + n [/math], для каждой итерации линейна, а для всего алгоритма в целом равна [math] N*n [/math], что позволяет сделать вывод о том, что перемещение данных для обработки не играет важной роли в данном алгоритме.

Для оптимизированного алгоритма вычислительная мощность так же линейна (приведение матрицы к форме Хессенберга имеет сложность [math] O(n^3) [/math], а объем выходных данных [math] O(n^2) [/math]).

Вычислительная погрешность растет линейно, из-за использования метода вращений для QR разложения.

Данный алгоритм недетерминирован, так как число итераций зависит от значений элементов матрицы и выход из основного цикла происходит по достижению некоторой точности. В зависимости от этого, вычислительный поток имеет различную длину. На каждой отдельной итерации в свою очередь алгоритм полностью детерминирован, так как детерминированы его обе базовые макрооперации - QR разложение и матричное умножение.

2 Программная реализация

2.1 Особенности реализации последовательного алгоритма

Основным типом данных для QR алгоритма является матрица. В данной статье представлена реализация на языке C++, что накладывает определенные ограничения на формат хранени матриц: все матрицы хранятся в одномерном массиве в построчном (ROW_MAJOR) формате.

В простейшем случае QR-алгоритм выглядит следующим образом:

int sequential_QR_algorithm(float *A, int size)
{
    float *Q = new double[size * size];
    float *R = new double[size * size];
    while(!check_if_upper_triangular(A, size)))
    {
        sgeqrf (ROW_MAJOR, size, size, A, size, tau);
        set_Q_and_R(A, Q, R, size);
        sorgqr(ROW_MAJOR, size, size, size, Q, size, tau);
        sgemm (RowMajor, NoTrans, NoTrans, size, size, size, 1, R, size, Q, size, 0, A, size);
    }
}

В последовательном случае функции dgeqrf, dorgqr и dgemm представляют собой последовательные функции стандарта BLAS, вычисляющие QR разложение(geqrf), матрицу Q после разложения (dorgqr) и матричное умножение (dgemm). Так же здесь используются простейшие функции set_Q_and_R и check_if_upper_triangular. Функция set_Q_and_R получает после QR разложения из матрицы A данные о матрицах Q и R. Функция check_if_upper_triangular проверяет, приведена ли матрица A к треугольном виду, и если да, происходит выход из цикла.

Для работы программы в памяти необходимо хранить 3 матрицы, таким образом общий объем составляет 3 * n^2. Так же необходим вспомогательный массив tau для QR разложения, однако его размер составляет всего n. Так же важно заметить, что различные реализации функций dgeqrf, dorgqr и dgemm обычно используют внутренние вспомогательные массивы для блочной обработки, однако, их размер не превышает n * C, где C - некоторая архитектурно зависимая константа.

Все вычисления рекомендуется производить в одинарной точности.

Как уже говорилось ранее, внешний цикл представленной программы сугубо последователен (итеративен), и основной ресурс параллелизма расположен в вызываемых функциях (geqrf, gemm). Их реализации бывают крайне различны, поэтому данный алгоритм можно легко преобразовать для любой архитектуры, используя набор стандартных библиотечных функций. К примеру, для реализации алгоритма на GPU можно использовать библиотеку MAGMA, на многоядерных CPU - Intel MKL.

2.3 Возможные способы и особенности параллельной реализации алгоритма

Как уже говорилось в разделе 2.1, при использовании различных библиотек можно реализовать данный алгоритм практически на всех архитектурах. Далее более подробно будут рассмотрены примеры для некоторых из них. Особенности параллельных реализаций для базовых макроопераций (QR разложения и матричного умножения), уже описаны в соответствующих статьях (см. ссылки в разделе 1.4)

Реализация на многоядерных CPU (одном узле)

Для распарарллеливания на многоядерных CPU используются функции LAPACKE_sgeqrf, LAPACKE_sorgqr и cblas_sgemm. Распараллеливание оставшихся функций может быть произведено с использованием openMP, так как внутренние циклы в них независимы по данным.

Исходный код предложенной реализации представлен далее:

int CPU_QR_algorithm(float *A, int size)
{
    float *Q = new double[size * size];
    float *R = new double[size * size];
    while(!check_if_upper_triangular(A, size)))
    {
        LAPACKE_sgeqrf (LAPACK_ROW_MAJOR, size, size, A, size, tau);
        set_Q_and_R(A, Q, R, size);
        LAPACKE_sorgqr(LAPACK_ROW_MAJOR, size, size, size, Q, size, tau);
        cblas_sgemm (CblasRowMajor, CblasNoTrans, CblasNoTrans, size, size, size, 1, R, size, Q, size, 0, A, size);
    }
}

Реализация на GPU (и multi-GPU)

Для реализации алгоритма на GPU и multi-GPU можно использовать аналогичные функции dgemm и geqrf из библиотеки magma.

2.4 Масштабируемость алгоритма и его реализации

2.4.1 Масштабируемость реализации алгоритма

Для данного алгоритма была проверена масштабируемость оптимизированной версии с приведением матрицы к форме Хессенберга. Тесты проводились для случайно сгенерированной матрицы размера 8000x8000 на 1-14 параллельных вычислительных потоках.

Код, для которого проверлась масштабируемость, реализован с помощью функций библиотеки intel MKL, выглядит следующим образом:

#include "stdio.h"
#include "stdlib.h"
#include "mkl.h"
#include "math.h"
#include <iostream>

using namespace std;

int main(int argc, char* argv[])
{
    int max_threads;
    float *h, *Wr, *Wi, *z, *scalar, *h_copy;
    double s_initial, s_elapsed;
    lapack_int n = atoi(argv[1]); //size=n
    
    h=(float*)mkl_malloc(n*n*sizeof(float),32);
    h_copy=(float*)mkl_malloc(n*n*sizeof(float),32);
    z=(float*)mkl_malloc(n*n*sizeof(float),32); //z will not be referenced due to set compz="N"
    Wr=(float*)mkl_malloc(n*sizeof(float),32);
    Wi=(float*)mkl_malloc(n*sizeof(float),32);
    scalar=(float*)mkl_malloc((n-1)*sizeof(float),32);
    if(h==NULL) //initilization for hessenberg matrix
    {
        for(int i=0;i<n*n;i++)
        {
            h[i]=(float)rand()*2000;
            h_copy[i]=h[i];
        }
    }
    for(int j=0;j<n*n;j++)
    {
        z[j]=0.0;
    }
    max_threads=mkl_get_max_threads();
    
    for(int t = 1;t <= max_threads;t++)
    {
        double t1 = dsecnd();
        mkl_set_num_threads(t);
        LAPACKE_sgehrd(LAPACK_ROW_MAJOR, n, 1, n, h, n, scalar);
        LAPACKE_shseqr(LAPACK_ROW_MAJOR, 'E', 'N', n, 1, n, h, n, Wr, Wi, z, n);
        double t2 = dsecnd();

        cout << "total time for " << t << " threads: " << t2 - t1 << endl << endl;

        for(int k=0;k<n*n;k++)
        {
            h[k]=h_copy[k];
        }
    }
    return 0;
}

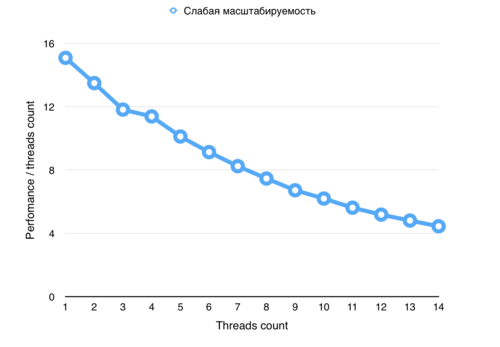
Далее приводятся графики сильной и слабой масштабируемости.

Рис.4 Сильная масштабируемость оптимизированного QR алгоритма с приведением матрицы к форме Хессенберга

Из данных графика видно, что алгоритм хорошо масштабируется при небольшом числе процессов (1-4), однако дальнейшее прибавление процессов не ведет к линейному ускорению.

2.7 Существующие реализации алгоритма

Последовательный QR алгоритм, а так же различные базовые функции для его реализации, можно найти в библиотеке LAPACK и её аналогах и расширениях.

Базовая версия QR алгоритма может быть реализована описанным в разделе 2.1 способом при помощи функций:

1. ?geqrf - вычисляет QR разложение произвольной матрицы
2. ?gemm - вычисляет произведение двух плотных матриц

?steqr - вычисляет собственные числа и собственные вектора для случая тридиагональной матрицы.

Для реализации оптимизированного алгоритма с приведением матрицы к матрице Хессенберга можно использовать следующие функции:

1. ?gehrd - приводят матрицу общего вида к верхней матрице Хессенберга с использованием ортогональных/унитарных трансформаций
2. ?hseqr - вычисляют собственные значения матрицы в верхней матрице Хессенберга с использованием QR алгоритма

Подробная документация по упомянутым функциям может быть найдена здесь.

Параллельный QR алгоритм может быть реализован с помощью библиотек ScaLAPACK и PlaLAPACK.

p?geqrf, p?gemm, p?hseqr - аналогичные функции ScaLAPACK.

PLA_QR, PLA_Gemm - аналогичные функции из PlaLAPACK.