Участник:Ilya4870/Алгоритм разбиения графа методом рекурсивной координатной бисекции

Эта работа прошла предварительную проверку Дата последней правки страницы: 16.11.2016 Данная работа соответствует формальным критериям. Проверено Dan.

Основные авторы описания: Габдуллина М.И. (1.1, 1.3, 1.5, 1.9, 2.7), Урюпов И.В. (1.2, 1.4, 1.6, 1.7, 1.8, 1.10), группа м218.

1 Свойства и структура алгоритмов

1.1 Общее описание алгоритма

Задача рациональной декомпозиции расчетных сеток возникает при численном моделировании на высокопроизводительных вычислительных системах проблем механики сплошных сред, импульсной энергетики, электродинамики и многих других. Такие задачи сводятся к более общей задачи - разбиение вершин графа. Оптимальным считается разбиение на домены, при котором выровнен суммарный вес вершин в доменах и минимизирован суммарный вес разрезанных ребер (разрезанное ребро – ребро, соединяющее вершины из разных доменов). Одним из методов разбиения вершин графа на равные по мощности блоки является метод рекурсивной координатной бисекции.

На каждом этапе рекурсивной бисекции область разбивается на две части. Соотношение размеров частей зависит от количества доменов, которые должны быть образованы в каждой из частей. Полученные подобласти разбиваются дальше аналогичным образом до тех пор, пока в подобластях не останется по одному домену. При рекурсивной координатной бисекции на этапе разбиения выбирается координатная ось, вдоль которой область имеет наибольшую протяженность. Область разбивается перпендикулярно полученной оси. Достоинством данного метода является то, что при разбиении на равные домены числа вершин в получаемых доменах отличаются не больше, чем на единицу. Другими достоинствами являются экономичное использование памяти и относительная быстрота работы.

1.2 Математическое описание алгоритма

Пусть [math]G = (V,E)[/math] – неориентированный граф, где [math]V = \{v_i\}[/math] – множество вершин, [math]E = \{e_{ij}\}[/math] – множество рёбер. И вершины, и рёбра, имеют целочисленные веса [math]|v_i|[/math] и [math]|e_{ij}|[/math], соответственно.

Декомпозиция является отображением множества вершин [math]V[/math] на заданное число [math]p[/math] доменов [math]S_j[/math] такое, что каждая вершина [math]v_i[/math] принадлежит некоторому домену [math]S_j[/math], и [math]S_k \cap S_m = \emptyset[/math].

Суммарный вес вершин в домене [math]S_j[/math] равен сумме весов вершин, принадлежащих этому домену: [math]|S_j| = \sum_{i}{|v_i|}, v_i \in S_j[/math].

Суммарный вес разрезанных рёбер равен сумме весов рёбер, соединяющих вершины из разных доменов: [math]|E_c|=\sum_{ij}{|e_ij|}, v_i \in S_k, v_j \in S_m, k \lt m[/math].

Каждый домен [math]S_j[/math] является некоторым подграфом [math]G^j = (V^j, E^j)[/math] графа [math]G = (V, E)[/math], где [math]V^j \subseteq V, E^j \subseteq E[/math]. Домен является связным, если его граф состоит из одной компоненты связности, то есть между любой парой вершин этого графа существует как минимум один путь.

Требуется найти такое разбиение множества вершин [math]V[/math] на заданное число [math]p[/math] связных доменов [math]S_j[/math], при котором:

• выровнен суммарный вес вершин в доменах: [math]|S_j| \approx |V|/p[/math],[math](1)[/math]

• минимизирован суммарный вес разрезанных рёбер: [math]min(|E_c|)[/math].[math](2)[/math]

Используя обозначения выше, определим:

• Входные данные алгоритма: множество координат вершин [math]C = \{c_i\}[/math] графа [math]G = (V, E)[/math], где [math]c_i = (v_i^x, v_i^y, v_i^z)[/math] - координаты вершины [math]v_i \in V[/math], число доменов [math]p[/math].

• Выходные данные алгоритма: разбиение множества вершин [math]V[/math] на заданное число [math]p[/math] доменов [math]S_j[/math].

Основные этапы алгоритма:

• вычисляются протяжённости осей: [math]l_k = |max(v_i^k) - min(v_i^k)|[/math] для [math]k = x, y, z[/math],

• производится сортировка множества [math]C[/math] по координате, соответствующей наибольшей [math]l_k[/math],

• множество [math]C[/math] разбивается на две части в соответствии с новым порядком элементов, то есть перпендикулярно координатной оси, вдоль которой она имеет наибольшую протяжённость; соотношение размеров частей зависит от количества доменов, которые должны быть образованы в каждой из частей,

• полученные подмножества разбиваются дальше аналогичным образом до тех пор, пока на очередном шаге рекурсии в них не останется по одному домену.

1.3 Вычислительное ядро алгоритма

Большую часть времени занимает сортировка массива координат вершин [math]C[/math], выполняемая на каждом шаге рекурсии. Сортировка может быть выполнена любым способом, в зависимости от реализации. В дальнейшем положим, что используется алгоритм с оптимальной вычислительной сложностью [math]O(nlog_2{n})[/math].

1.4 Макроструктура алгоритма

Как записано и в описании ядра алгоритма, основную часть метода составляют сортировки массивов координат вершин [math]C[/math], выполняемые на каждом шаге рекурсии.

1.5 Схема реализации последовательного алгоритма

1. Вычисляются минимумы и максимумы по каждой из координат, определяющие параллелепипед, охватывающий вершины данной области. Далее запускается процесс рекурсии, на каждом шаге которого выполняется следующее:
   1. Определяется координата [math]j[/math], вдоль которой параллелепипед, обрабатывающийся на данном этапе, имеет наибольшую протяженность.
   2. Определяется количество доменов, которое делится на данном этапе. В левую часть (вершины с меньшей координатой [math]j[/math]) попадет половина доменов. Сначала набираются домены нулевого типа, потом, если они закончились, первого, и т.д. до получения нужного числа доменов в левой части. Подсчитывается общее число вершин n1, которое окажется в этих доменах. В правой части будут сформированы оставшиеся домены.
   3. Пусть все вершины в параллелепипеде имеют координаты [math]j[/math], принадлежащие интервалу [math][j_{min}, j_{max}][/math]. Интервал делится на [math]K[/math] равных малых интервалов. [math]K[/math] – некоторая константа. Подсчитываются количества вершин, принадлежащие каждому малому интервалу. Исходя из того, что в левую часть должна попасть [math]n_1[/math] вершина с меньшей координатой [math]j[/math], определяется, в какой малый интервал [math][j_{from}, j_{to}][/math] попадает медиана. Затем вершины из интервала [math][j_{from}, j_{to}][/math] записываются в отдельный массив, отсортированный по всем координатам. Определяется медиана – последняя вершина, которая попадет в левую часть.
   4. Если предполагается построение локальных деревьев, для вершины [math]i[/math] двоичного дерева запоминаются данные о медиане: ее координаты, номер вершины медианы и номер координаты [math]j[/math], по которой проводилось деление.
   5. Проводится разделение данных по аналогии с обменной сортировкой с разделением Хоару (быстрая сортировка), чтобы на следующих этапах просматривались только вершины из разбиваемой области. Два указателя, [math]begin[/math] и [math]end[/math], выставляются на начало и на конец массива данных, соответственно. Вершина, на которую указывает указатель [math]begin[/math], сравнивается с медианой по всем координатам, и, если она попадает в левую часть параллелепипеда, указатель [math]begin[/math] сдвигается к следующей вершине. Так до тех пор, пока указатель [math]begin[/math] не остановится на вершине, которая должна попасть в правую часть. Указатель [math]end[/math] конца массива сдвигается влево до тех пор, пока не остановится на вершине, которая должна попасть в левую часть. Если указатель [math]begin[/math] находится левее указателя [math]end[/math], вершины, на которые указывают указатели, меняются местами, после чего указатель [math]begin[/math] сдвигается вправо, а [math]end[/math] – влево.Если указатель [math]begin[/math] все еще левее указателя [math]end[/math], весь процесс повторяется снова. Если после выхода из цикла указатели указывают на одну и ту же вершину, она сравнивается с медианой по всем координатам, и если вершина попадает в левую часть, указатель [math]begin[/math] сдвигается к следующей вершине. Указатель [math]begin[/math] определяет начало массива данных правой части.
2. По рекурсии левая и правая части отправляются на деление. Левой части передается указатель на начало исходного массива данных и число вершин [math]n_1[/math]. Максимальные координаты параллелепипеда остаются теми же, только максимальная координата [math]j[/math] приравнивается к координате [math]j[/math] медианы. Передается число доменов каждого вида, которое будет в левой части. Номер вершины двоичного дерева, отвечающей за деление левой части, будет равным [math]2i[/math]. Правой части передается указатель [math]begin[/math] в качестве нового указателя на массив данных и оставшееся число вершин. Минимальная координата [math]j[/math] приравнивается к координате медианы. Передаются числа доменов каждого вида. Номер вершины двоичного дерева, отвечающей за деление правой части, будет равным [math]2i + 1[/math].
3. Перед делением каждой из частей проверяется, сколько доменов осталось в данной части. Если остался только один домен, то все вершины помещаются в данный домен. Домены считаются по порядку от номера [math]gr_0[/math] первого домена. Если предполагается построение локальных деревьев, в лист дерева записывается номер домена. Запоминается максимальный номер вершины. Если в части осталось больше одного домена, она отправляется на деление.

Рисунок 1. Пример координатной бисекции на три домена.

Алгоритм работает только с координатами вершин и не учитывает связи между ними, что делает его экономичным по памяти.

1.6 Последовательная сложность алгоритма

Для разбиения графа с количеством вершин [math]n[/math] методом рекурсивной координатной бисекции на [math]p[/math] доменов требуется:

• для каждого шага рекурсии:
  • определить максимум и минимум координат, [math]O(n)[/math] операций сравнения,
  • отсортировать подобласть по одной из координат, [math]O(nlog_2{n})[/math] операций сравнения.

Глубина рекурсии - [math]log_2{p}+1[/math].

Сравнения составляют основную часть алгоритма.

Таким образом, алгоритм имеет последовательную сложность [math]O(n, p) = n \log_2{n} \log_2{p}.[/math]

1.7 Информационный граф

Опишем граф алгоритма в виде рисунка.

Рисунок 2. Информационный граф алгоритма. In - входные данные,LS - локальная сортировка, PS - параллельная сортировка с помощью сортировочной сести, D - декомпозиция, Out - выходные данные

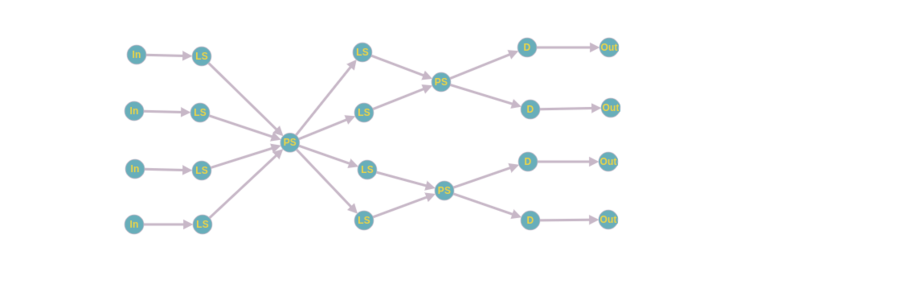
Граф алгоритма состоит из двух групп вершин, соответствующих бисекции по процессам (LS и PS) и локальной бисекции на каждом процессе (D). Первая группа делится на подгруппы, каждая подгруппа содержит некоторое количество сетей параллельной сортировки (PS), каждая из которых может выполнятся независимо от других. Во второй же группе вершин все операции в одной вершине не зависят от других вершин.

1.8 Ресурс параллелизма алгоритма

Исходя из того, что метод является геометрическим, алгоритм обладает координатным параллелизмом. Таким образом структура параллельного алгоритма включает в себя следующие этапы:

1. Начальное распределение вершин по процессорам. Начальное распределение может быть любым, например, в соответствии с порядковыми номерами вершин.
2. Определение числа доменов, которые должны быть сформированы на каждом из процессоров, и количества вершин в них.
3. Рекурсивная координатная бисекция вершин по процессорам. На каждом этапе сначала вычисляется координатная ось, вдоль которой область имеет наибольшую протяженность. Затем блок вершин бьется на две части перпендикулярно данной оси. Группа процессоров делится на две, далее каждая из групп делит свой блок вершин аналогичным образом. Для разделения блока вершин используется параллельная сортировка. После рекурсивной координатной бисекции вершин по процессорам на процессорах оказывается столько вершин, сколько должно быть в образуемых на них доменах.
4. Локальная рекурсивная координатная бисекция вершин по доменам. Дальнейшее разбиение на домены проводится локально на каждом процессоре.

Для разбиения графа [math]G=(V, E), |V|=n[/math] на [math]p[/math] доменов в параллельном варианте при количестве процессов [math]N_p[/math] требуется последовательно выполнить следующие ярусы:

• для бисекции по процессам — [math]log_2{N_p}[/math] пар ярусов, содержащих:
  • локальную сортировку, при количестве вершин [math]n, \frac{n}{2}, \frac{n}{4},\ldots;[/math]
  • параллельную сеть сортировки, при количестве элементов [math]n, \frac{n}{2}, \frac{n}{4},\ldots[/math], при количестве процессов [math]N_p, \frac{N_p}{2}, \frac{N_p}{4},\ldots;[/math]
• один ярус, содержащий локальную бисекцию на каждом процессе для количества вершин [math]\frac{n}{N_p}.[/math]

Таким образом, параллельный вариант алгоритма обладает двухступенчатой структурой. При классификации по высоте ЯПФ его сложность — [math]O\left(\left[m \log_2{m} + \frac{1}{2} \log_2{n} (\log_2{n} + 1)\right]\log_2{N_p} + m \log_2{m} \log_2{p}\right)[/math], где [math]m=\frac{n}{N_p}[/math]. При классификации по ширине ЯПФ его сложность будет [math]O(N_p)[/math].

1.9 Входные и выходные данные алгоритма

Входные данные алгоритма: множество координат вершин [math]C = \{c_i\}[/math] графа [math]G = (V, E)[/math], где [math]c_i = (v_i^x, v_i^y, v_i^z)[/math] - координаты вершины [math]v_i \in V[/math]. Таким образом, множество координат вершин может быть передано как массив трёхмерных векторов. Число доменов [math]p[/math] передается в виде натурального числа, не может превышать число вершин.

Количество элементов массива входных данных может быть очень большим, например, алгоритм используется для нерегулярных сеток, содержащих [math]10^9[/math] и более вершин. В настоящее время такие сетки невозможно разместить в памяти одного процессора (на гексаэдральную сетку, состоящую из [math]1.2 \cdot 10^8[/math] ячеек, требуется порядка 200 ГБ), поэтому для декомпозиции нужен параллельный алгоритм.

Число процессоров, на котором будет считаться вычислительная задача, как правило, заранее неизвестно. Поэтому имеет смысл предварительно однократно разбить сетку на большое число микродоменов, а потом формировать из них домены. Количество микродоменов на несколько порядков меньше числа вершин, поэтому многократное разбиение микродоменов на домены быстрее многократного разбиения всей сетки.

Выходные данные алгоритма: разбиение множества вершин [math]V[/math] на заданное число [math]p[/math] доменов [math]S_j[/math]. Эти данные могут быть записаны как массив четырехмерных векторов координат вершин, четвертой координатой будет номер домена, которому принадлежит вершина.

1.10 Свойства алгоритма

Алгоритм детерминирован в случае использования устойчивой сортировки вершин. Алгоритм устойчив, так как работает с целочисленными данными, ошибки округления отсутствуют.

Вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных, равна [math]O(\log_2{n} \log_2{p})[/math], где [math]n[/math] - количество вершин в графе, [math]p[/math] - количество доменов.

Так как основной операцией алгоритма является сравнение целых чисел при сортировке, наблюдается дисбаланс арифметических операций по отношению к операциям обращения к памяти. Алгоритм обладает сбалансированностью операций между параллельными ветвями алгоритма, что следует из условия [math](1)[/math] - количество вершин на разных процессах примерно одинаково.

Дуги информационного графа, исходящие из вершины, соответствующей сети сортировки с номером [math]k[/math], имеют степень [math]\frac{N_p}{2^k}, k = 0, 1,\ldots, \log_2{N_p}[/math]. Это означает, что их степень убывает в ходе работы алгоритма от [math]N_p[/math] до [math]1[/math].

2 Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

Проведём исследование масштабируемости параллельной реализации алгоритма разбиения графа методом рекурсивной координатной бисекции согласно методике. Исследование проводилось на суперкомпьютере "BlueGene/P", с использованием библиотеки Zoltan2.

Набор и границы значений параметров запуска реализации алгоритма:

• число процессоров [1 : 512] с множителем 2;
• количество вершин в графе - [math]1.5 /dot 10^7[/math];
• количество доменов - 2048.

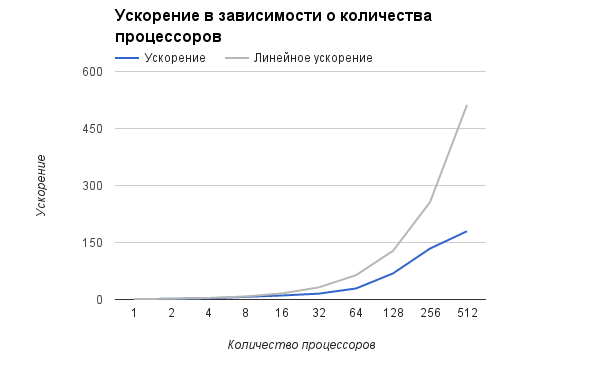
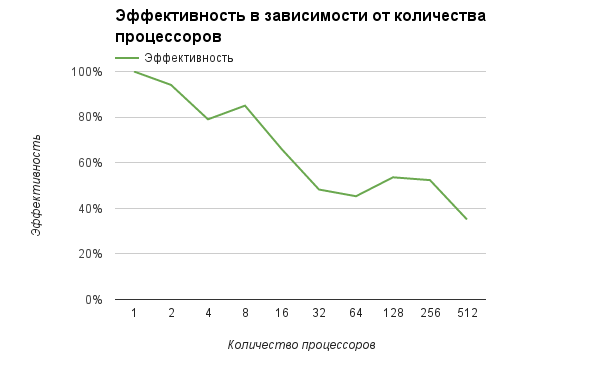
В результате проведённых экспериментов был получен следующий диапазон эффективности реализации алгоритма:

• минимальная эффективность реализации [math]35%[/math];
• максимальная эффективность реализации [math]94%[/math].

На следующих рисунках приведены графики ускорения и эффективности выбранной реализации алгоритма разбиения графа методом рекурсивной координатной бисекции в зависимости от числа процессоров.

Рисунок 3. Ускорение алгоритма разбиения графа методом рекурсивной координатной бисекции в зависимости от числа процессоров.

Рисунок 4. Эффективность алгоритма разбиения графа методом рекурсивной координатной бисекции в зависимости от числа процессоров.

Построим оценку масштабируемости выбранной реализации алгоритма разбиения графа методом рекурсивной координатной бисекции.

• По числу процессов: [math]-0,0131[/math]. При увеличении числа процессов эффективность на рассмотренной области изменений параметров запуска уменьшается. Уменьшение эффективности на рассмотренной области работы параллельной программы объясняется быстрым ростом накладных расходов на организацию параллельного выполнения.

2.7 Существующие реализации алгоритма

Алгоритм, как и многие другие алгоритмы разбиения графов реализованы в следующих последовательных пакетах декомпозиции графов: METIS, JOSTLE, SCOTCH, CHACO и PARTY. К параллельным пакетам относятся PARMETIS (параллельная версия пакета METIS), JOSTLE, PT-SCOTCH (параллельная версия пакета SCOTCH) и ZOLTAN.

ParMETIS и METIS распространяются свободно URL: http://glaros.dtc.umn.edu/gkhome/software .

ZOLTAN - свободная лицензия, URL: http://www.cs.sandia.gov/~web1400/1400_download.html .

Также алгоритм реализован в параллельном пакете GridSpiderPar, URL: http://lira.imamod.ru/FondProgramm/Decomposition/