Участник:DenisAnuprienko/Метод Штрассена
Основные авторы описания: Д.В.Ануприенко.
Общая схема описания алгоритмов имеет следующий вид:
Содержание
- 1 Свойства и структура алгоритмов
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритмов
1.1 Общее описание алгоритма
Метод Штрассена предназначен для умножения матриц. Здесь будет рассмотрен вариант метода, который можно применять к квадратным матрицам размера [math]N = 2^n[/math]. В таком случае две матрицы можно умножить быстрее, чем за [math]O(N^3)[/math].
1.2 Математическое описание алгоритма
Пусть имеются две матрицы [math]A, B \in \mathbb{R}^{N\times N}[/math]. Представим их в блочном виде:
[math]
A =
\begin{bmatrix}
A_{11} & A_{12}\\
A_{21} & A_{22}\\
\end{bmatrix},
B =
\begin{bmatrix}
B_{11} & B_{12}\\
B_{21} & B_{22}\\
\end{bmatrix}.
[/math]
При обычном умножении матриц пришлось бы совершить 8 умножений подматриц порядка [math]N/2[/math]. В методе Штрассена предлагается обойтись всего 7 умножениями. Находятся 7 вспомогательных подматриц [math]M_1, ..., M_7[/math] по следующим формулам:
[math]
M_1 = (A_{11} + A_{22})(B_{11} + B_{22})
[/math]
[math]
M_2 = (A_{21} + A_{22})B_{11}
[/math]
[math]
M_3 = A_{11}(B_{12} - B_{22})
[/math]
[math]
M_4 = A_{22}(B_{21} - B_{11})
[/math]
[math]
M_5 = (A_{11} + A_{12})B_{22}
[/math]
[math]
M_6 = (A_{21} - A_{22})(B_{11} + B_{12})
[/math]
[math]
M_7 = (A_{12} - A_{22})(B_{21} + B_{22})
[/math]
После этого матрица [math]C[/math], являющаяся произведением [math]A[/math] и [math]B[/math], находится по формулам
[math]
C_{11} = M_1 + M_4 - M_5 + M_7
[/math]
[math]
C_{12} = M_3 + M_5
[/math]
[math]
C_{21} = M_2 + M_4
[/math]
[math]
C_{22} = M_1 - M_2 + M_3 + M_6
[/math]
Если и умножения подматриц, необходимые для нахождения [math]M_i[/math], проводить по такой же схеме, получается рекурсивный алгоритм. Всего в нем понадобится выполнить [math]O(7^{log_2N}) = O(N^{log_27}) \approx O(N^{2.81})[/math] умножений. На практике рекурсию можно не разворачивать до конца, а использовать обычное умножение уже на матрицах размера 512.
[math][/math]
1.3 Вычислительное ядро алгоритма
Основное время работы алгоритма приходится на формирование множителей для умножения подматриц, рекурсивные вызовы и умножение матриц обычным методом в конце рекурсии.
1.4 Макроструктура алгоритма
1.5 Схема реализации последовательного алгоритма
- Если размер матриц меньше или равен некоторого числа [math]N_{min}[/math], умножить их обычным способом.
- Иначе
- Сформировать множители для матрицы [math]M_1[/math]
- Применить метод Штрассена для этих множителей
- Сформировать множители для матрицы [math]M_2[/math]
- Применить метод Штрассена для этих множителей
- ...
- Сформировать множители для матрицы [math]M_7[/math]
- Применить метод Штрассена для этих множителей
- Сформировать результат из матриц [math]M_1, ..., M_7[/math].
1.6 Последовательная сложность алгоритма
Метод Штрассен позволяет сократить число умножений, поэтому оценивается именно оно. В методе Штрассена число умножений составляет [math]O(7^{log_2N}) = O(N^{log_27}) \approx O(N^{2.81})[/math].
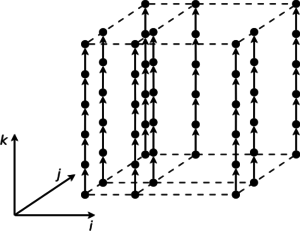
1.7 Информационный граф
Это очень важный раздел описания. Именно здесь можно показать (увидеть) как устроена параллельная структура алгоритма, для чего приводится описание и изображение его информационного графа (графа алгоритма [1]). Для рисунков с изображением графа будут составлены рекомендации по их формированию, чтобы все информационные графы, внесенные в энциклопедию, можно было бы воспринимать и интерпретировать одинаково. Дополнительно можно привести полное параметрическое описание графа в терминах покрывающих функций [1].
Интересных вариантов для отражения информационной структуры алгоритмов много. Для каких-то алгоритмов нужно показать максимально подробную структуру, а иногда важнее макроструктура. Много информации несут разного рода проекции информационного графа, выделяя его регулярные составляющие и одновременно скрывая несущественные детали. Иногда оказывается полезным показать последовательность в изменении графа при изменении значений внешних переменных (например, размеров матриц): мы часто ожидаем "подобное" изменение информационного графа, но это изменение не всегда очевидно на практике.
В целом, задача изображения графа алгоритма весьма нетривиальна. Начнем с того, что это потенциально бесконечный граф, число вершин и дуг которого определяется значениями внешних переменных, а они могут быть весьма и весьма велики. В такой ситуации, как правило, спасают упомянутые выше соображения подобия, делающие графы для разных значений внешних переменных "похожими": почти всегда достаточно привести лишь один граф небольшого размера, добавив, что графы для остальных значений будут устроены "точно также". На практике, увы, не всегда все так просто, и здесь нужно быть аккуратным.
Далее, граф алгоритма - это потенциально многомерный объект. Наиболее естественная система координат для размещения вершин и дуг информационного графа опирается на структуру вложенности циклов в реализации алгоритма. Если глубина вложенности циклов не превышает трех, то и граф размещается в привычном трехмерном пространстве, однако для более сложных циклических конструкций с глубиной вложенности 4 и больше необходимы специальные методы представления и изображения графов.
В данном разделе AlgoWiki могут использоваться многие интересные возможности, которые еще подлежат обсуждению: возможность повернуть граф при его отображении на экране компьютера для выбора наиболее удобного угла обзора, разметка вершин по типу соответствующим им операций, отражение ярусно-параллельной формы графа и другие. Но в любом случае нужно не забывать главную задачу данного раздела - показать информационную структуру алгоритма так, чтобы стали понятны все его ключевые особенности, особенности параллельной структуры, особенности множеств дуг, участки регулярности и, напротив, участки с недерминированной структурой, зависящей от входных данных.
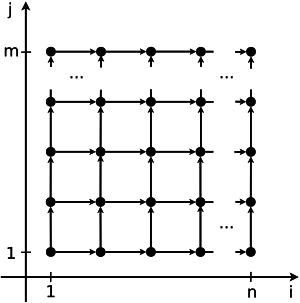
На рис.1 показана информационная структура алгоритма умножения матриц, на рис.2 - информационная структура одного из вариантов алгоритма решения систем линейных алгебраических уравнений с блочно-двухдиагональной матрицей.
1.8 Ресурс параллелизма алгоритма
Умножения, которые необходимы для нахождения матриц [math]M_1, ..., M_7[/math], можно провести параллельно. Их можно предоставить 7 узлам (1 хозяин, который раздает задания 6 рабочим и получает результаты, а также работает вместе с ними) или 8 узлам (1 хозяин, который раздает задания 7 рабочим и получает результаты).
1.9 Входные и выходные данные алгоритма
Нет никаких предположений насчет структуры матриц. Предполагается, что это обычные плотные матрицы. Они хранятся в виде одномерного массива, что позволяет легко выделять из них подматрицы.
1.10 Свойства алгоритма
- Алгоритм устойчив
- Алгоритм детерминирован
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
Все действия с двумя главными матрицами проводит только процесс-хозяин. Каждый процесс также создает и освобождает для себя вспомогательные матрицы [math]M_i[/math], а также две матрицы для записи множителей для нахождения [math]M_i[/math].
2.3 Возможные способы и особенности параллельной реализации алгоритма
Устройство метода Штрассена накладывает ограничения на количество узлов для распараллеливания.
- Как уже было отмечено, распараллеливать можно 7 умножений, из которых получаются матрицы [math]M_1, ..., M_7[/math], с помощью 7 или 8 процессов.
- Распараллеливание этих 7 умножений с помощью меньшего, чем 7, или большего, чем 8, числа процессов не рассматривается, так как в первом случае количество пересылок будет тем же, а время работы - большим, а во втором случае получается более 1 процесса на 1 умножение, что является дополнительным усложнением с негарантированной пользой.
- В таком случае, распараллеливание [math]n[/math] уровней рекурсии требует как минимум [math]7^n[/math] узлов. Количество узлов меняется тогда и только тогда, когда меняется число распараллеливаемых уровней рекурсии.
- Здесь будет рассмотрен вариант метода Штрассена, где распараллеливается 1 уровень рекурсии с помощью 8 процессов: 1 хозяина и 7 рабочих. Эта версия работает несколько быстрее, чем версия с 7 процессами.
2.4 Масштабируемость алгоритма и его реализации
По описанным в предыдущем пункте причинам предлагаемая реализация с распараллеливанием 1 уровня рекурсии может быть запущена только на определенном количестве узлов. Запуск на другом количестве узлов означает использование уже другой программы, поэтому оценить масшатбируемость в текущей реализации не представляется возможным.
2.5 Динамические характеристики и эффективность реализации алгоритма
Это объемный раздел AlgoWiki, поскольку оценка эффективности реализации алгоритма требует комплексного подхода [2], предполагающего аккуратный анализ всех этапов от архитектуры компьютера до самого алгоритма. Основная задача данного раздела заключается в том, чтобы оценить степень эффективности параллельных программ, реализующих данный алгоритм на различных платформах, в зависимости от числа процессоров и размера задачи. Эффективность в данном разделе понимается широко: это и эффективность распараллеливания программы, это и эффективность реализации программ по отношению к пиковым показателям работы вычислительных систем.
Помимо собственно показателей эффективности, нужно описать и все основные причины, из-за которых эффективность работы параллельной программы на конкретной вычислительной платформе не удается сделать выше. Это не самая простая задача, поскольку на данный момент нет общепринятой методики и соответствующего инструментария, с помощью которых подобный анализ можно было бы провести. Требуется оценить и описать эффективность работы с памятью (особенности профиля взаимодействия программы с памятью), эффективность использования заложенного в алгоритм ресурса параллелизма, эффективность использования коммуникационной сети (особенности коммуникационного профиля), эффективность операций ввода/вывода и т.п. Иногда достаточно интегральных характеристик по работе программы, в некоторых случаях полезно показать данные мониторинга нижнего уровня, например, по загрузке процессора, кэш-промахам, интенсивности использования сети Infiniband и т.п. Хорошее представление о работе параллельной MPI-программы дают данные трассировки, полученные, например, с помощью системы Scalasca.
2.6 Выводы для классов архитектур
В данный раздел должны быть включены рекомендации по реализации алгоритма для разных классов архитектур. Если архитектура какого-либо компьютера или платформы обладает специфическими особенностями, влияющими на эффективность реализации, то это здесь нужно отметить.
На практике это сделать можно по-разному: либо все свести в один текущий раздел, либо же соответствующие факты сразу включать в предшествующие разделы, где они обсуждаются и необходимы по смыслу. В некоторых случаях, имеет смысл делать отдельные варианты всей части II AlgoWiki применительно к отдельным классам архитектур, оставляя общей машинно-независимую часть I. В любом случае, важно указать и позитивные, и негативные факты по отношению к конкретным классам. Можно говорить о возможных вариантах оптимизации или даже о "трюках" в написании программ, ориентированных на целевые классы архитектур.
2.7 Существующие реализации алгоритма
Для многих пар алгоритм+компьютер уже созданы хорошие реализации, которыми можно и нужно пользоваться на практике. Данный раздел предназначен для того, чтобы дать ссылки на основные существующие последовательные и параллельные реализации алгоритма, доступные для использования уже сейчас. Указывается, является ли реализация коммерческой или свободной, под какой лицензией распространяется, приводится местоположение дистрибутива и имеющихся описаний. Если есть информация об особенностях, достоинствах и/или недостатках различных реализаций, то это также нужно здесь указать. Хорошими примерами реализации многих алгоритмов являются MKL, ScaLAPACK, PETSc, FFTW, ATLAS, Magma и другие подобные библиотеки.