Участник:Vvnikolaev/Решето Эратосфена

1 Свойства и структура алгоритмов

1.1 Общее описание алгоритма

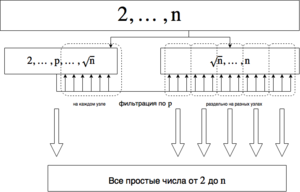
Решето́ Эратосфе́на — алгоритм нахождения всех простых чисел до некоторого целого числа [math]n[/math]. Приписывается древнегреческому математику Эратосфену Киренскому (откуда и название). Алгоритм проходит список всех чисел от [math]2[/math] до [math]n[/math] и на каждом шаге убирает часть чисел, не являющихся простыми. Таким образом происходит фильтрация («решето» в названии).

1.2 Математическое описание алгоритма

Пусть требуется найти все простые числа от [math]2[/math] до [math]n[/math]. Алгоритм состоит из следующих шагов:

1. Выписываются подряд все натуральные числа от [math]2[/math] до [math]n[/math]
2. Положим [math]p = 2[/math]
3. Зачеркиваются числа от [math]2p[/math] до [math]n[/math] с шагом [math]p[/math] (то есть все числа от [math]2[/math] до [math]n[/math], кратные [math]p[/math])
4. Ищется первое не зачеркнутое число в списке, превышающие [math]p[/math], и это значение присваивается переменной [math]p[/math]
5. Повторяются шаги 3 и 4 пока возможно

На практике на шаге 3 зачеркивать числа можно начиная с [math]p^2[/math], и, соответственно алгоритм заканчивает свою работу при [math]p^2 \gt n[/math].

1.3 Вычислительное ядро алгоритма

Основное время работы приходится на шаг №3 алгоритма. Можно показать, что сложность составляет [math]O(nlog(log(n)))[/math].

1.4 Макроструктура алгоритма

Алгоритм можно разбить на 2 части:

1. Первая часть — создается булев массив длины n и заполняется единицами
2. Вторая часть — последовательно рассматривается каждое, еще не помеченное число, и с помощью него производится фильтрация бо́льших чисел

1.5 Схема реализации последовательного алгоритма

Псевдокод вычислительного ядра алгоритма:

Вход: натуральное число n

Пусть A — булев массив, индексируемый числами от 2 до n, изначально заполненный значениями true.

 для i := 2, 3, 4, ..., пока i2 ≤ n:
  если A[i] = true:
    для j := i2, i2 + i, i2 + 2i, ..., пока j ≤ n:
      A[j] := false

Выход: числа i, для которых A[i] = true.

1.6 Последовательная сложность алгоритма

Сложность алгоритма складывается из двух составляющих. Первое — выписывание всех чисел от [math]2[/math] до [math]n[/math]. Это, очевидно, делается за [math]O(n)[/math]. Вторая составляющая — повторение шагов 3 и 4 — вычислительное ядро алгоритма. Сложность этой части составляет [math]O(nlog(log(n)))[/math]. Строгое доказательство этого факта можно найти в книге Hardy и Wright «An Introduction to the Theory of Numbers».

1.7 Информационный граф

Информационный граф рассматриваемого алгоритма:

1.8 Ресурс параллелизма алгоритма

Вычислительное ядро алгоритма можно распараллелить, но не полностью. Разобьем все натуральные числа [math]\{2, \dots, n\}[/math] на 2 множества — [math]\{2, \dots, \sqrt n\}[/math] и [math]\{\sqrt n + 1\dots, n\}[/math]. Поиск простых чисел на первом множестве распараллелить нельзя, а на втором — можно (различия заключаются в том, что числа из второго множества не будут проверяться в качестве делителей — они все больше [math] \sqrt n [/math]). Поэтому проверка на простоту для первого множества будет выполняться на каждом потоке, а второе можно разбить на [math]p[/math] частей ([math]p[/math] — количество процессов) и проверять каждую часть на простоту отдельно. Так как первая часть при больших [math]n[/math] значительно меньше второй, то можно предположить, что параллельное выполнение даст хороший прирост к скорости.

1.9 Входные и выходные данные алгоритма

Входные данные алгоритма — одно число [math]n[/math], до которого нужно найти все простые числа. На выходе алгоритм выдает либо булев массив длины [math]n[/math], отражающий для каждого натурального числа, является ли оно простым, либо список простых чисел от [math]2[/math] до [math]n[/math] (что конкретно — зависит от реализации и не имеет особого значения).

2 Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

Задача данного раздела - показать пределы масштабируемости алгоритма на различных платформах. Очень важный раздел. Нужно выделить, описать и оценить влияние точек барьерной синхронизации, глобальных операций, операций сборки/разборки данных, привести оценки или провести исследование сильной и слабой масштабируемости алгоритма и его реализаций.

Масштабируемость алгоритма определяет свойства самого алгоритма безотносительно конкретных особенностей используемого компьютера. Она показывает, насколько параллельные свойства алгоритма позволяют использовать возможности растущего числа процессорных элементов. Масштабируемость параллельных программ определяется как относительно конкретного компьютера, так и относительно используемой технологии программирования, и в этом случае она показывает, насколько может вырасти реальная производительность данного компьютера на данной программе, записанной с помощью данной технологии программирования, при использовании бóльших вычислительных ресурсов (ядер, процессоров, вычислительных узлов).

Ключевой момент данного раздела заключается в том, чтобы показать реальные параметры масштабируемости программы для данного алгоритма на различных вычислительных платформах в зависимости от числа процессоров и размера задачи . При этом важно подобрать такое соотношение между числом процессоров и размером задачи, чтобы отразить все характерные точки в поведении параллельной программы, в частности, достижение максимальной производительности, а также тонкие эффекты, возникающие, например, из-за блочной структуры алгоритма или иерархии памяти.

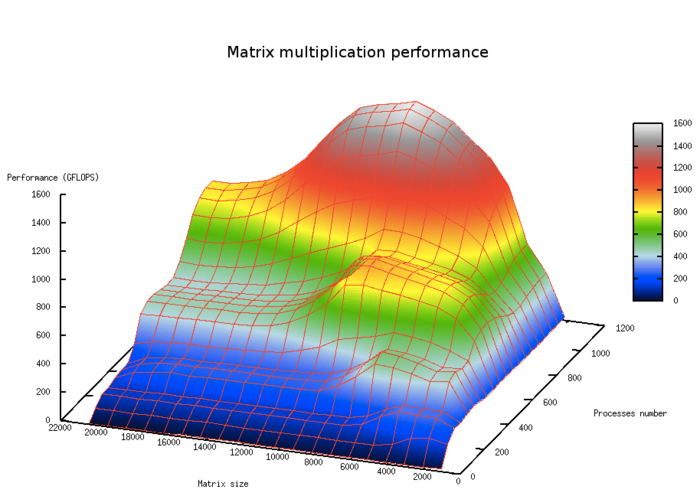
На рис.5. показана масштабируемость классического алгоритма умножения плотных матриц в зависимости от числа процессоров и размера задачи. На графике хорошо видны области с большей производительностью, отвечающие уровням кэш-памяти.

Рис.5 Масштабируемость классического алгоритма умножения плотных матриц в зависимости от числа процессоров и размера задачи

2.7 Существующие реализации алгоритма

Однопоточные реализации с различными улчшениями:

1. Однопоточная реализация с некоторыми улучшениями: http://e-maxx.ru/algo/eratosthenes_sieve
2. Однопоточная реализация, работающая за сублинейное время: http://e-maxx.ru/algo/prime_sieve_linear

Многопоточные реализации:

1. https://github.com/keyfunda/primes-parallel-sieve
2. https://github.com/Heliosmaster/BSPEratosthenes
3. https://github.com/marius92mc/sieve-of-eratosthenes-with-MPI