Участник:Sarseev/Алгоритм кластеризации, основанный на минимальном покрывающем дереве

Автор: Арсеев С. П., группа 620

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Данный алгоритм нацелен на решение задачи кластеризации, то есть, разделения множества объектов на группы, называемые кластерами, так, чтобы внутри одного кластера оказались наиболее похожие (по некоторой метрике) друг на друга объекты, а объекты из разных кластеров как можно сильнее отличались друг от друга. Сам алгоритм состоит из следующих шагов:

1. Сведение набора объектов к графу. Объекты становятся вершинами графа, и каждые две вершины соединяются ребром, длина которого равняется расстоянию между этими объектами по некоторой метрике. Выбор метрики зависит от предметной области и желаемых свойств алгоритма. Например, метрикой может служить евклидово расстояние.
2. Построение минимального покрывающего (остовного) дерева в этом графе. Более подробно этот шаг описан в соответствующей статье.
3. Кластеризация путём удаления некоторого количества рёбер в этом дереве. В случае, если заранее известно количество кластеров [math]k[/math], достаточно удалить [math]k-1[/math] ребро с наибольшей длиной, чтобы получить [math]k[/math] связных компонент, которые объявляются кластерами. Если же количество кластеров заранее не известно, удаляются рёбра с длиной больше некоторого порога, задаваемого как параметр алгоритма. Возможны и более сложные стратегии выбора рёбер для отсечения.

1.2 Математическое описание алгоритма

На вход алгоритму подаётся [math]n[/math] объектов [math]a[/math], которые нужно кластеризовать. Каждый такой объект можно рассматривать как вектор или элемент некоторого метрического пространства. На пространстве, которому принадлежат [math]a[/math], задана метрика [math]d_{ij}=d(a_i,a_j)[/math].
Первый шаг алгоритма строит граф [math]G=(V,E)[/math], где [math]V[/math] - множество вершин графа [math](|V|=n)[/math], а [math]E[/math] - множество его рёбер [math](|E| = \frac{n*(n-1)}{2})[/math].
На втором этапе строится минимальное покрывающее дерево [math]MST(G)[/math]. После удаления рёбер дерево распадается на поддеревья [math]MST_i[/math]. Вершины, входящие в [math]i[/math]-е поддерево, объявляются принадлежащими кластеру с номером [math]i[/math].

1.3 Вычислительное ядро алгоритма

Алгоритм состоит из трёх этапов:

1. Преобразование исходных данных. Сложность [math]O(n^2)[/math].
2. Поиск минимального покрывающего дерева. Последовательная сложность всех трёх основных алгоритмов (Борувки, Крускала и Прима) [math]O(|E|*log(|E|)) = O(n^2*log(n^2))[/math].
3. Разбиение на кластеры. Вычислительная сложность [math]O(n)[/math] для простых стратегий разбиения.

Таким образом, вычислительным ядром алгоритма является алгоритм построения минимального покрывающего дерева, поскольку он имеет наибольшую сложность. Стратегии распараллеливания алгоритма основаны на распараллеливании алгоритма построения минимального покрывающего дерева.

1.4 Макроструктура алгоритма

В состав алгоритма входит алгоритм построения минимального покрывающего дерева, являющийся его вычислительным ядром. Также в отдельную часть можно выделить алгоритм разбиения получившегося покрывающего дерева на кластеры.

1.5 Схема реализации последовательного алгоритма

Описание алгоритма на псевдокоде:

MST_Cluster(object[n] objects){
    g = Pairs(objects, metric);
    mst = Create_MST(graph);
    parts = Split_MST(mst);
    for i in range(parts){
         clusters[i] = parts[i].vertices;
    }
    return clusters
}

1.6 Последовательная сложность алгоритма

Последовательная сложность алгоритма определяется самой сложной его частью (см. пункт 1.3) и равна [math]O(n^2*log(n^2))[/math].

1.7 Информационный граф

Информационный граф алгоритма. Показана последовательная реализация (большой прямоугольник) и схема распараллеливания алгоритма построения минимального покрывающего дерева.

1.8 Ресурс параллелизма алгоритма

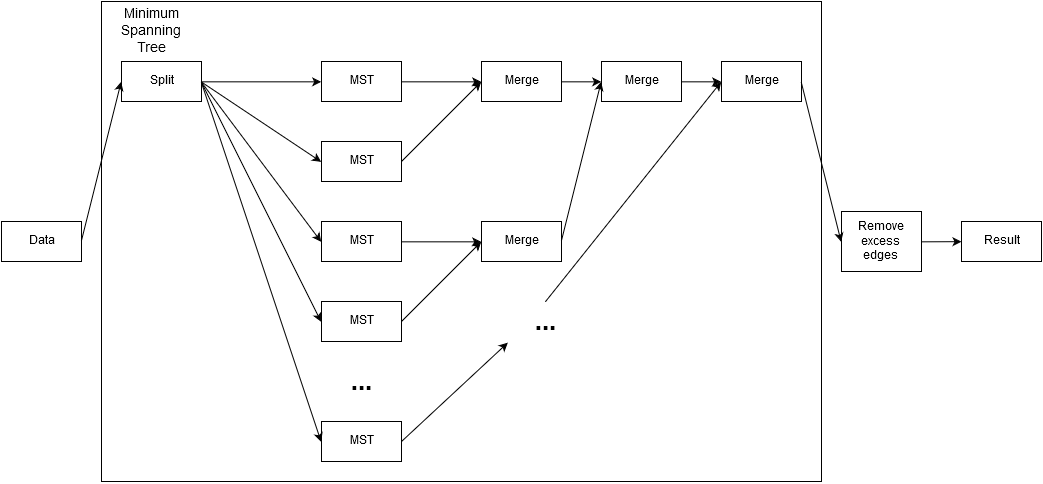
Ресурс параллелизма алгоритма основан на свойстве ассоциативности рёбер:
Пусть [math]MSF(E)[/math] – минимальный остовный лес (множество покрывающих деревьев) графа с рёбрами [math]E[/math]. Тогда

[math] MSF(E_1 \cup E_2 \cup \dots \cup E_k) = MSF(MSF(E_1) \cup MSF(E_2) \cup \dots \cup MSF(E_k)). [/math]

Параллельная схема вычисления устроена следующим образом:

1. Рёбра графа распределяются между процессами.
2. Каждый процесс строит минимальный остовный лес из своих рёбер.
3. После этого полученные остовные леса объединяются в единое покрывающее дерево для всего графа, как показано на информационном графе.

Сложность параллельного алгоритма зависит от соотношения объёма входных данных и числа процессов. Существуют распределённые алгоритмы построения минимального покрывающего дерева, имеющие асимптотическую сложность [math]O(n*log(n))[/math]. Эта же оценка будет выполняться и для всего алгоритма кластеризации.

1.9 Входные и выходные данные алгоритма

На вход алгоритму подаются объекты [math](o_1, o_2, ..., o_n)[/math].
Выходом алгоритма является множество непересекающихся кластеров: [math]C=(C_1, C_2, ..., C_k); C_i = (o_{i,1}, o_{i,2}, ..., o_{i, n_i}); o(i, l) \ne o(j, m); i \ne j; \forall l, m; \sum{n_i} = n [/math].

1.10 Свойства алгоритма

Важным свойством алгоритма является то, что при его распараллеливании по описанной выше стратегии важно правильно выбирать количество процессов. При увеличении количества процессов возрастают затраты на фазу слияния деревьев, полученных каждым процессом: растёт число этапов, в которые производится слияние, а следовательно, возрастают затраты на коммуникацию между процессами, и распределение нагрузки становится более неравномерным из-за того, что часть процессов должна проделать значительно большее количество работы по слиянию деревьев.
Вычислительная мощность алгоритма имеет порядок [math]O(n*log(n^2))[/math].
Ещё одним важным свойством алгоритма является его детерминированность в том случае, если для данного набора векторов существует единственное минимальное покрывающее дерево: при использовании детерминированной стратегии разбиения его на поддеревья алгоритм получает единственный результат для каждого набора данных. Однако, время работы может отличаться в зависимости от начального распределения рёбер по процессам.

2 Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

Время работы алгоритма в зависимости от числа процессов и объёма входных данных.

Время работы алгоритма при меньшем числе процессов и объёме входных данных.

Эффективность распараллеливания алгоритма.

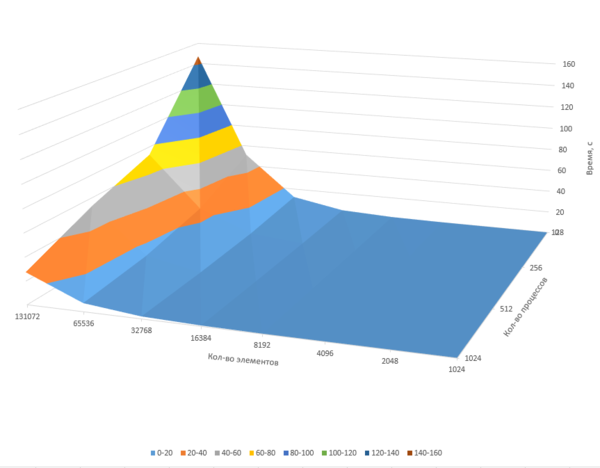
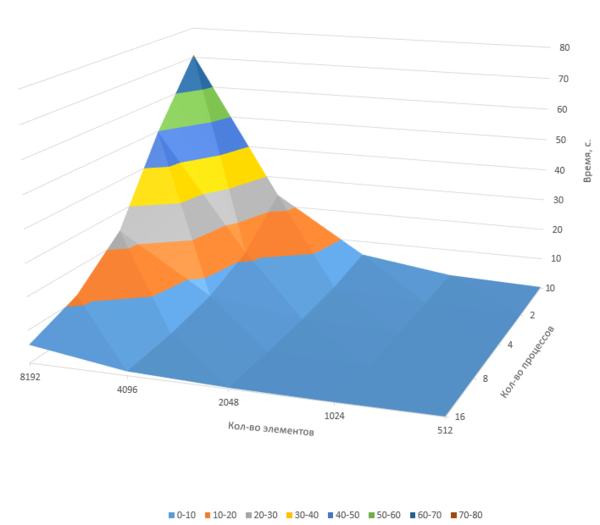
На первом и втором графике на логарифмической шкале показана зависимость времени работы алгоритма от числа процессов. Приведены измерения для девфти наборов данных, различающихся количеством входных векторов: от 512 до 131072 элементов. Использовалась собственная реализация алгоритма, основанная на сторонней реализации алгоритма построения минимального покрывающего дерева (без OpenMP-части для более точного измерения масштабируемости описанной выше архитектуры). Изменения относительно приведённой реализации в основном коснулись генерации входных данных для алгоритма построения остовного дерева: в качестве функции расстояния между элементами при генерации графа бралось случайное число от 0 до 1. Изменения времени работы алгоритма при разных запусках (и, соответственно, с другим набором случайных чисел) незначительны.
Полный текст изменённой части программы расположен по адресу [1].
Запуск проводился на аппаратной платформе IBM BlueGene/P. Для каждого размера входных данных были проведены четыре теста: на 128, 256, 512 и 1024 вычислительных узлах соответственно. При дальнейшем увеличении объёма данных время выполнения программы превысило доступный предел (15 минут для 128 узлов).
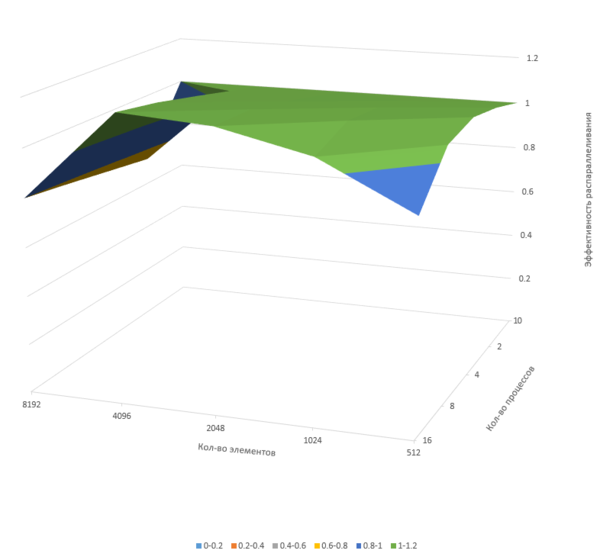
На третьем графике показана зависимость эффективности распараллеливания алгоритма в зависимости от числа вычислительных уздов и объёма входных данных. Видно, что эффективность быстро падает для малого объёма входных данных (из-за возрастающих затрат на обмен информацией) и остаётся высокой на графе из 2048 вершин.

2.7 Существующие реализации алгоритма

Основным вычислительным ядром алгоритма является алгоритм построения минимального покрывающего (остовного) дерева, применяющийся для многих задач, и многие библиотеки ограничиваются его реализацией, без реализации основанного на нём алгоритма кластеризации. Примеры реализаций алгоритмов построения MST:

• С++: Boost graph library (алгоритмы Борувки и Крускала)
• C++, MPI: Parallel boost graph library (алгоритм Борувки)
• Java: JGraphT (алгоритмы Крускала и Прима)
• Python: SciPy

3 Литература

1. Нейский И.М. Классификация и сравнение методов кластеризации
   
2. C. Kingsford. Minimum Spanning Trees & Clustering ([2])
3. Y. Zhou et al. Clustering with Minimum Spanning Trees