Участник:Pandvik/Ортогонализация Грама - Шмидта

Эта работа успешно выполнена Преподавателю: в основное пространство, в подстраницу Данное задание было проверено и зачтено. Проверено Frolov и ASA.

Авторы описания алгоритма: Павлов Андрей (разделы [1.7], [1.8], [2.4], [2.7], [3] - поиск и изучение литературы), Филимонов Владимир (разделы [1.1]-[1.6], [1.9], [1.10], [2.7], [3] - поиск и изучение литературы).

Ортогонализация Грамма-Шмидта [1]
Последовательный алгоритм
Последовательная сложность	[math]O(N^2M)[/math]
Объём входных данных	[math]NM[/math]
Объём выходных данных	[math]NM[/math]

1 ЧАСТЬ. Свойства и структура алгоритмов

1.1 Общее описание алгоритма

В конечномерном евклидовом пространстве существует ортонормированный базис.

Для доказательства этого факта требуется находить и строить такие базисы. Построить ортонормированный базис можно, отталкиваясь от некоторого исходного базиса, при помощи алгоритма, который называют процессом ортогонализации Грама — Шмидта.

Процесс ортогонализации Грама-Шмидта используется для квадратных невырожденных матриц, которые преобразуются, либо уже преобразованы, к верхнему(нижнему) треугольному виду.

Процесс ортогонализации Грама-Шмидта нашёл применение в оптимизации оценивания параметров моделей управления объектом, в протоколах безопасности, в обработке сигналов, в вычислении локальных минимумов целочисленных решёток и многом другом.

Обычно, процесс ортогонализации используется как промежуточный шаг в других алгоритмах для уменьшения количества вычислений.

1.2 Математическое описание алгоритма

Исходные данные: квадратная матрица A с линейно независимыми векторами [math]\mathbf{a}_1,...,\mathbf{a}_N | \mathbf{a}_i \in \R^{M}[/math].

Определяется оператор проекции [math]\mathbf{proj}_b a = \frac{\left \langle a,b \right \rangle}{\left \langle b,b \right \rangle }b[/math], где [math]\left \langle a,b \right \rangle[/math] - скалярное произведение векторов a и b. Данный оператор используется для проецирования вектора a коллинеарно вектору b.

[math]\mathbf{b}_1 = \mathbf{a}_1[/math]

[math]\mathbf{b}_2 = \mathbf{a}_2 - \mathbf{proj}_{\mathbf{b}_1} \mathbf{a}_2 [/math]

[math]\mathbf{b}_3 = \mathbf{a}_3 - ( \mathbf{proj}_{\mathbf{b}_1} \mathbf{a}_3 + \mathbf{proj}_{\mathbf{b}_2} \mathbf{a}_3 )[/math]

[math]\mathbf{b}_4 = \mathbf{a}_4 - ( \mathbf{proj}_{\mathbf{b}_1} \mathbf{a}_4 + \mathbf{proj}_{\mathbf{b}_2} \mathbf{a}_4 + \mathbf{proj}_{\mathbf{b}_3} \mathbf{a}_4 )[/math]

[math]\vdots[/math]

[math]\mathbf{b}_N = \mathbf{a}_N - \sum_{j=1}^{N-1} \mathbf{proj}_{\mathbf{b}_j} \mathbf{a}_N[/math]

На основе каждого вектора [math]\mathbf{b}_j (j = 1 \cdots N)[/math] может быть получен нормированный вектор [math]\mathbf{e}_j = \frac{\mathbf{b}_j}{||\mathbf{b}_j||}[/math].

Результаты процесса ортогонализации Грама-Шмидта: [math]\mathbf{b}_1\cdots\mathbf{b}_N[/math] - система ортогональных векторов либо система ортонормированных векторов [math]\mathbf{e}_1\cdots\mathbf{e}_N[/math].

Подробное описание можно найти в .

1.3 Вычислительное ядро алгоритма

Основная вычислительная сложность данного алгоритма заключается в вычислении суммы проекций векторов [math]\sum_{j=1}^{i-1} \mathbf{proj}_{\mathbf{b}_j} \mathbf{a}_N[/math] для каждого [math]b_i[/math].

Подробное описание общей сложности алгоритма представлено в разделе #Последовательная сложность алгоритма

1.4 Макроструктура алгоритма

1. первый ортогональный вектор [math]\mathbf{b}_1[/math] задаётся с помощью координат вектора [math]\mathbf{a}_1[/math];

2. второй ортогональный вектор получаем с помощью вычитания из [math]\mathbf{a}_2[/math] проекции полученного ортогонального вектора [math]\mathbf{b}_1[/math] на [math]\mathbf{a}_2[/math];

[math]\vdots[/math]

N. каждый новый ортогональный вектор получаем с помощью вычитания из [math]\mathbf{a}_N[/math] суммы проекций полученных предыдущих векторов [math]\mathbf{b}_1 \cdots \mathbf{b}_{N-1}[/math] на [math]\mathbf{a}_N[/math], где [math]\mathbf{a}_1 \cdots \mathbf{a}_{N}[/math] - векторы исходной матрицы [math]A[/math], а [math]\mathbf{b}_1 \cdots \mathbf{b}_{N}[/math] - получаемые ортогональные векторы матрицы [math]B[/math].

Как можно заметить из #Математическое описание алгоритма, в алгоритме преобладают векторные вычисления. Ключевым этапом процесса ортогонализации Грама-Шмидта является вычисление большого числа проекций для каждого вектора, каждый из которых состоит из трёх операций сложения и одной операции деления. В свою очередь, можно сделать вывод, что основную часть представленного метода составляют вычисления проекций векторов и сумм этих проекций [math]\sum_{j=1}^{N-1} \mathbf{proj}_{\mathbf{b}_j} \mathbf{a}_N[/math], где [math]\mathbf{proj}_b a = \frac{\left \langle a,b \right \rangle}{\left \langle b,b \right \rangle }b[/math].

1.5 Схема реализации последовательного алгоритма

Пусть дано множество векторов [math]{a_1, a_2, \cdots , a_N}[/math]. Тогда:

Шаг 1: [math]\mathbf{b}_1 = \mathbf{a}_1[/math]

Для вычисления остальных [math]\mathbf{b}_i [/math] следует последовательно выполнять Шаг 2 для всех [math] i [/math] таких что при [math] 2 \le i \le N [/math].

Шаг 2: [math]\mathbf{b}_i = \mathbf{a}_i - \sum_{j=1}^{i-1} \mathbf{proj}_{\mathbf{b}_{j}} \mathbf{a}_i[/math], где для каждого [math]\mathbf{proj}_b a[/math] выполняется [math]\frac{\left \langle a,b \right \rangle}{\left \langle b,b \right \rangle}b[/math].

1.6 Последовательная сложность алгоритма

Оценим сложность последовательной реализации алгоритма.

Для вычисления одной операции проекции требуется:

[math]{\color{Blue}\bullet} \quad M \cdot 3[/math] - умножений;

[math]{\color{Blue}\bullet} \quad (M-1) \cdot 2[/math] - сложений;

[math]{\color{Blue}\bullet} \quad 1 [/math] - деление;

Общее число операций, необходимых для вычисления алгоритма следующее:

[math]{\color{Blue}\bullet} \quad \frac{N(N-1)}{2} \cdot M \cdot 3[/math] - умножений;

[math]{\color{Blue}\bullet} \quad \frac{N(N-1)}{2} \cdot (M-1) \cdot 3 [/math] - сложений и вычитаний;

[math]{\color{Blue}\bullet} \quad \frac{N(N-1)}{2} [/math] - делений.

Исходя из вышесказанного, получаем итоговую сложность последовательного алгоритма [math]O(N^2 \cdot M)[/math].

1.7 Информационный граф

Опишем информационный граф алгоритма. В разделе #Схематичное описание информационного графа будет представлена схема с сокрытием подробностей реализации функции проекции. Такое ограничение позволяет продемонстрировать основные зависимости, не перегружая картинку лишними элементами. В разделе #Уточнение информационного графа будет раскрыта внутренняя структура операции проекции.

1.7.1 Схематичное описание информационного графа

Для вычисления [math]b_i[/math] требуется найти [math]proj_{b_{j}}a_{i}[/math] для всех [math]j \in [1, i][/math]. Следовательно для полного вычисления вектора [math]b_{i}[/math] требуется знать все [math]b_{j}[/math] с меньшим индексом. Такая зависимость по данным очень не удачна для параллелизма. Однако, если разбить процесс вычисления [math]b_{i}[/math] на несколько этапов, соответствующих функциям проекции ([math]proj_{b_{j}}a_{i}[/math]), то это позволит производить некоторые предварительные вычисления для [math]b_{j}[/math] до момента, когда станут известны все предшествующие ей [math]b_{i}[/math].

Далее в этом разделе будут представлены несколько вариантов информационного графа. Общим моментом является выделение двойными фиолетовыми кругами данных, поступающих на вход, а двойными зелёными кругами - те данные, которые будут получены на выходе алгоритма. В предложенных графах, остриё стрелок указывает на элемент, которому требуются некоторые данные. То есть исходящие стрелки обозначают результат операции, а входящие - аргументы операции.

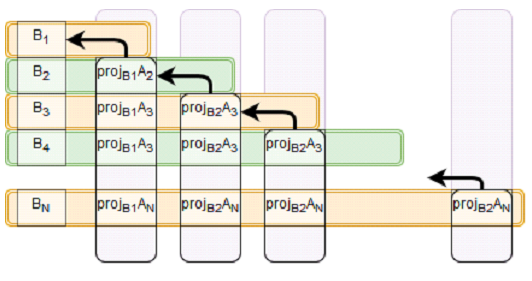
На Рис. 1 изображена зависимость каждого из этапов от предыдущих вычислений. Первая строка овалов содержит все проекции, зависящие от [math]b_{1}[/math], вторая строка - все проекции, зависящие от [math]b_{2}[/math], [math]\;\cdots\;[/math], самая верхняя строка содержит проекцию, которая зависит от [math]b_{N-1}[/math]. Широкие красные стрелки обозначают суммирование элементов с сохранением результата в переменную, находящуюся на острие стрелки. Следует уточнить, что в данном варианте графа указаны только зависимости по данным вычисляемым непосредственно в процессе работы алгоритма. Так, например, опущена зависимость проекций от векторов [math]a_{i}[/math], что позволяет сделать рисунок более наглядным.

Рис. 2 показывает зависимость по данным немного в другом формате. Каждая строка представляет собой набор данных, которые требуются для вычисления [math]b_{i}[/math] из первого столбца. Второй и последующие столбцы группируют проекции, зависящие от одной из [math]b_{i}[/math] и, с помощью стрелки, показывают эту зависимость. В данном варианте схемы зависимости по данным опущены входные данные, так как они изначально доступны для каждой вычислительной единицы.

Рис. 1. Информационный граф алгоритма Грама-Шмидта

Рис. 2. Информационный граф алгоритма Грама-Шмидта

1.7.2 Уточнение информационного графа

В этом разделе будет представлено уточнение информационной структуры графа изображенного на Рис. 1 с помощью раскрытия внутренней структуры операции проекции. Полученный граф несёт в себе новую информацию, которую можно использовать для улучшения алгоритма, но становится менее понятным.

На Рис. 3 изображен граф, аналогичный графу Рис. 1, но функция [math]proj[/math] изображена более подробно. Оранжевым овалом обозначаются скалярные произведения двух векторов. Голубой треугольник - принимает на вход два числа (являющиеся результатами скалярных произведений) и вычисляет их частное. Зелёным шестиугольником обозначается произведение вектора [math]a_i[/math] на число. Фиолетовый ромб складывает два числа, от которых имеется зависимость. Зелёными стрелками будут выделены потоки наиболее значимые для алгоритма потоки данных. А именно - распределение зависимостей от вычисленных векторов [math]b_i[/math]. Стрелки, показывающие зависимость от начальных векторов окрашены в серый цвет. Для всех стрелок ромбом обозначен исток стрелки, точкой обозначено ветвление стрелки.

По сравнению с Рис. 1, более детальное описание информационной модели позволяет заметить повторяющиеся построчно скалярные произведения [math](b_i, b_i)[/math]. Зависимость от такого скалярного произведения изображена красным цветом на Рис. 3. Это замечание позволяет уменьшить суммарное число операций, но увеличивает объём данных передаваемых между вычислительными элементами.

Рис. 3. Уточненный информационный граф алгоритма Грама-Шмидта

1.8 Ресурс параллелизма алгоритма

На основе графа зависимости по данным, представленном на Рис. 1 или Рис. 2 раздела #Информационный граф можно выделить следующий ресурс для параллелизации. После вычисления [math]b_{i}[/math] можно начинать параллельно вычислять все [math]proj_{b_i}a_{j}[/math]. На Рис. 2 блоки, которые можно вычислять параллельно представлены столбцами.

Кроме того, при очень больших размерностях можно также распараллелить вычисление проекций. Так как в функции проекции участвует пара векторов [math]a[/math] и [math]b[/math], а сама операция проекции определяется как [math]\mathbf{proj}_b a = \frac{\left \langle a,b \right \rangle}{\left \langle b,b \right \rangle }b[/math], где [math]\left \langle a,b \right \rangle[/math] - скалярное произведение векторов [math]a[/math] и [math]b[/math], то с помощью использования векторных операций можно получить некоторый выигрыш в производительности.

1.8.1 Оценка ускорения параллельной реализации алгоритма

Рассмотрим случай, когда присутствует возможность запуска бесконечного числа потоков. Попробуем оценить сложность вычисления ортогональных векторов, при условии, что параллельно будут запускаться все проекции использующие одинаковую [math]b_i[/math]. В этом случае, останется критический путь зависимости по данным: [math]b_1 \leftarrow proj_{b_2}a_{2} \leftarrow b_2 \leftarrow proj_{b_3}a_{3} \leftarrow \ldots \leftarrow proj_{b_{N-1}}a_{N-1} \leftarrow b_N[/math]. Следовательно для оценки сложность распараллеленной версии алгоритма достаточно почитать сложность представленной цепочки вычислений.

[math]{\color{Blue}\bullet} \quad M \cdot 3[/math] умножения в одной проекции;

[math]{\color{Blue}\bullet} \quad (M-1) \cdot 2[/math] сложения/вычитаний;

[math]{\color{Blue}\bullet} \quad 1[/math] деление;

В цепочке зависимости данных присутствует [math]N-1[/math] проекция, значит всего:

[math]{\color{Blue}\bullet} \quad N \cdot M \cdot 3[/math] - умножений;

[math]{\color{Blue}\bullet} \quad N \cdot (M-1) \cdot 2[/math] - сложений/вычитаний;

[math]{\color{Blue}\bullet} \quad N \cdot 1[/math] - делений.

Получаем итоговую сложность [math]O(N \cdot M)[/math].

Если дополнительно рассматривать возможность параллелизации векторных операций (скалярного произведения и умножения вектора на число), критический путь можно сократить до следующих операций:

[math]{\color{Blue}\bullet} \quad 3 \cdot N [/math] умножений;

[math]{\color{Blue}\bullet} \quad N [/math] делений;

[math]{\color{Blue}\bullet} \quad N \cdot logM [/math] сложений;

Следовательно оценка сложности параллельного алгоритма станет равна [math]O(N \cdot logM)[/math].

1.9 Входные и выходные данные алгоритма

Входные данные: прямоугольная матрица [math]A^{M \times N}[/math] (элементы [math]\mathbf{a}_{ij}[/math]).

Ограничение: матрица [math]A[/math] должна быть невырожденной.

Объём входных данных: [math] N \cdot N[/math].

Выходные данные: матрица [math]B[/math] (система ортогональных векторов [math]\mathbf{b}_{1} \cdots \mathbf{b}_{N}[/math]).

Объём выходных данных: [math]N \cdot N[/math].

1.10 Свойства алгоритма

Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов : [math]\frac{N^2 \cdot M}{N \cdot log M} = \frac{N \cdot M}{log M}[/math].

Отношение числа операций к суммарному объему входных и выходных данных - линейное.

Представленный алгоритм является численно неустойчивым в силу ошибок округления, которые накапливаются в суммах проекций, так как они могут привести к неортогональности всей системы. Чтобы исправить численную неустойчивость требуется для каждого искомого вектора [math]\mathbf{b}_j[/math] делать переортагонализацию вектора путём последовательного вычитания из [math]\mathbf{a}_j[/math] компенент по направлению [math]\mathbf{b}_j[/math]. В результате внесённых изменений из формулы [math]\mathbf{b}_j = \mathbf{a}_j - \sum_{i=1}^{j-1} \mathbf{proj}_{\mathbf{b}_i} \mathbf{a}_j[/math] получаем вычисления следующего вида:

[math]\mathbf{a}_j^{(1)}[/math] = [math]\mathbf{a}_j[/math] - [math]\mathbf{proj}_{\mathbf{b}_1} \mathbf{a}_j[/math]

[math]\mathbf{a}_j^{(2)}[/math] = [math]\mathbf{a}_j^{(1)}[/math] - [math]\mathbf{proj}_{\mathbf{b}_1} \mathbf{a}_j^{(1)}[/math]

[math]\vdots[/math]

[math]\mathbf{a}_j^{(j-2)}[/math] = [math]\mathbf{a}_j^{(j-3)}[/math] - [math]\mathbf{proj}_{\mathbf{b}_{j-2}} \mathbf{a}_j^{(j-3)}[/math]

[math]\mathbf{b}_j[/math] = [math]\mathbf{a}_j^{(j-2)}[/math] - [math]\mathbf{proj}_{\mathbf{b}_{j-1}} \mathbf{a}_j^{(j-2)}[/math] .

Существуют несколько реализаций рассматриваемого алгоритма. Статья описывает три версии данного алгоритма: строковый классический алгоритм Г-Ш (Грама - Шмидта), столбцовый классический алгоритм Г-Ш и модифицированный алгоритм Г-Ш. Также существует ортогонализация с использованием алгоритма SVD (примером является реализация данного метода в библиотеке SciPy - scipy.linalg.orth(A) [2]). Модифицированный алгоритм Грама-Шмидта является вычислительно более устойчивым, то есть позволяет уменьшить погрешность вычислений связанную с ошибкой выполнения операций с плавающей точкой.

Процесс Грама — Шмидта может применяться к линейно зависимым векторам. В этом случае он выдаёт [math] 0 [/math] (нулевой вектор) на шаге [math] j [/math], если [math]a_{j}[/math] является линейной комбинацией векторов [math]a_{1}, \ldots ,a_{j-1}[/math].

2 ЧАСТЬ. Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

2.4.1 Масштабируемость алгоритма

Теоретические оценки предела масштабируемости алгоритма были рассмотрены в разделе #Ресурс параллелизма алгоритма.

2.4.2 Масштабируемость реализации алгоритма

Проведём исследование масштабируемости параллельной реализации согласно методике. Исследование проводилось на суперкомпьютере "Ломоносов" Суперкомпьютерного комплекса Московского университета.

Набор и границы значений изменяемых параметров запуска реализации алгоритма:

• число процессоров [8 : 64] с шагом 4;
• размер матрицы [2000 : 7000] с шагом 500-1000.

В результате проведённых экспериментов был получен следующий диапазон эффективности распараллеливания алгоритма:

• минимальная эффективность реализации 0.58%;
• максимальная эффективность реализации 9.48%.

На следующих рисунках приведены графики времени работы и эффективности выбранной реализации алгоритма ортогонализации Грама-Шмидта в зависимости от изменяемых параметров запуска.

Рис. 4. График времени работы реализации алгоритма Грама-Шмидта (с использованием технологии MPI)

Рис. 5. График эффективности распараллеливания реализации алгоритма Грама-Шмидта относительно последовательной реализации

Таблица зависимости времени работы реализации от размерности задачи и числа вычислительных узлов

Время(сек.) | N | M | CPUS 8.214269 2000 2000 8 5.535392 2000 2000 16 7.121008 2000 2000 24 10.995030 2000 2000 32 17.709424 2000 2000 40 15.969897 2500 2500 8 9.438978 2500 2500 16 9.658329 2500 2500 24 12.944879 2500 2500 32 17.741019 2500 2500 40 25.414062 2500 2500 48 27.463480 3000 3000 8 15.192174 3000 3000 16 13.546558 3000 3000 24 14.893935 3000 3000 32 19.726213 3000 3000 40 27.127187 3000 3000 48 35.446089 3000 3000 56 43.528986 3500 3500 8 23.267714 3500 3500 16 18.832487 3500 3500 24 20.074890 3500 3500 32 22.985693 3500 3500 40 27.376960 3500 3500 48 37.711549 3500 3500 56 48.896100 3500 3500 64 64.889743 4000 4000 8 34.014309 4000 4000 16 25.912094 4000 4000 24 24.668768 4000 4000 32 27.262719 4000 4000 40 32.295430 4000 4000 48 41.851132 4000 4000 56 48.027403 4000 4000 64 92.075673 4500 4500 8 47.766134 4500 4500 16 35.229498 4500 4500 24 31.972291 4500 4500 32 33.277924 4500 4500 40 38.653318 4500 4500 48 45.888597 4500 4500 56 54.089960 4500 4500 64 126.197428 5000 5000 8 64.872589 5000 5000 16 46.852009 5000 5000 24 40.500379 5000 5000 32 39.817172 5000 5000 40 42.630904 5000 5000 48 48.521401 5000 5000 56 55.565563 5000 5000 64 85.984754 5500 5500 16 60.770627 5500 5500 24 50.246163 5500 5500 32 47.708869 5500 5500 40 49.754522 5500 5500 48 52.557597 5500 5500 56 59.170178 5500 5500 64 111.130398 6000 6000 16 77.988458 6000 6000 24 63.733449 6000 6000 32 57.554799 6000 6000 40 57.613826 6000 6000 48 62.380190 6000 6000 56 68.328533 6000 6000 64 121.137472 7000 7000 24 96.815082 7000 7000 32 84.331911 7000 7000 40 79.391282 7000 7000 48 78.346921 7000 7000 56 84.036373 7000 7000 64

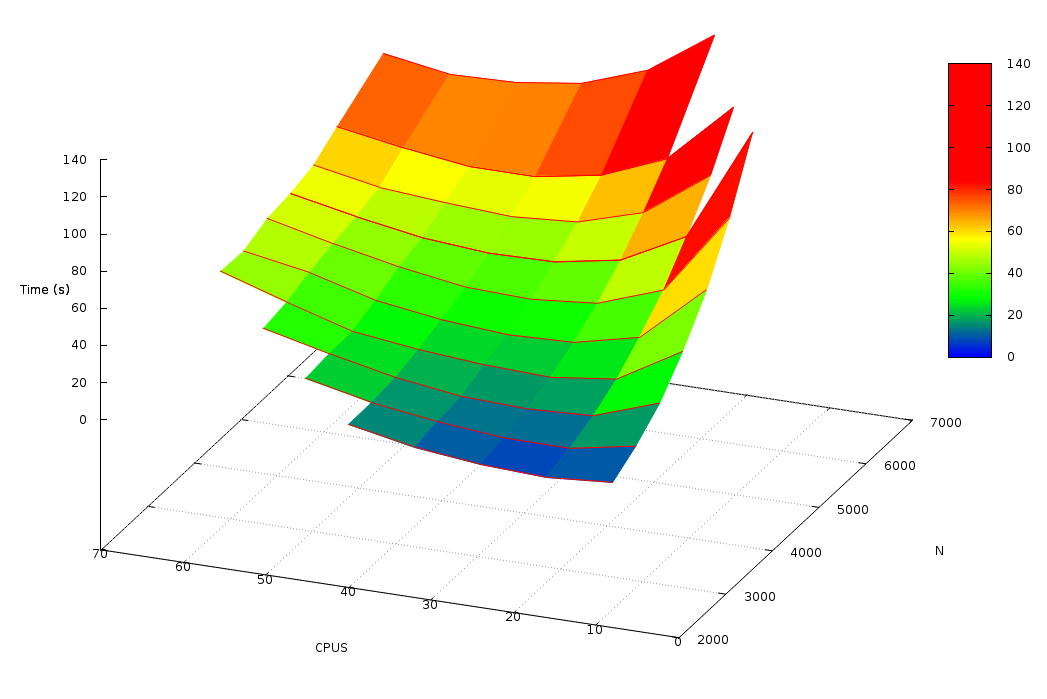
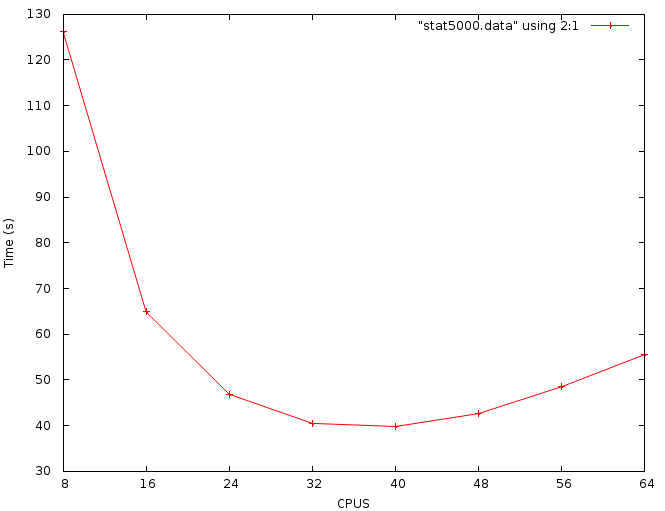
На Рис. 4 изображен график зависимости времени решения задачи от размерности входных данных и числа вычислительных узлов. При фиксированном значении размерности задачи, график зависимости времени работы реализации от числа узлов имеет вид вогнутой функции (пример для размерности матрицы 5000 изображен на Рис.6). То есть при увеличении числа узлов время работы данной реализации начинает увеличиваться после некоторого порогового значения, зависящего от размерности решаемой задачи. Есть предположение, что этот эффект является следствием большого объема данных, который передаётся между вычислительными узлами.

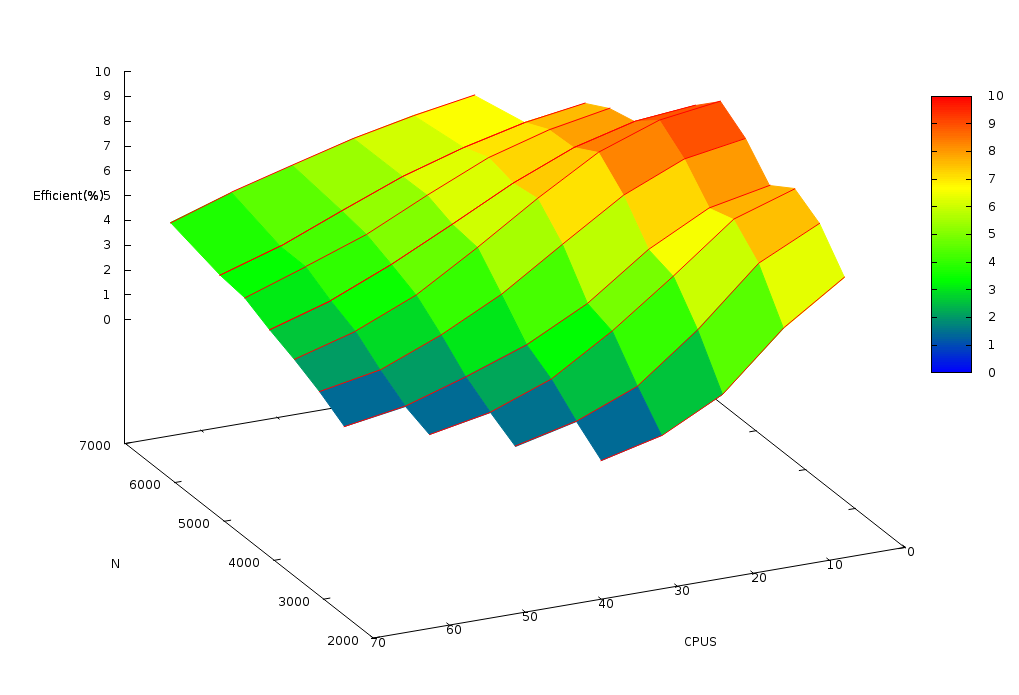
Рис. 5 изображает эффективность распараллеливания данной реализации в зависимости от размерности задачи и числа вычислительных узлов. По этому графику можно сделать вывод, что максимальная эффективность (9.5%) была достигнута на задаче размерности 4500 на 8 и 16 вычислительных узлах. Так же наблюдается снижение эффективности распараллеливания при увеличении числа вычислительных узлов.

На основе результатов тестирования можно определить число вычислительных узлов, на которых время работы рассматриваемой реализации является минимальным:

Размерность задачи:	2000	2500	3000	3500	4000	4500	5000	5500	6000	7000
Число узлов, на которых время работы данной реализации является минимальным:	16	16	24	24	32	32	40	40	40	56

Рис. 6. График времени работы параллельной реализации алгоритма Грама-Шмидта при размерности исходной матрицы 5000x5000

2.4.3 Особенности тестирования реализации алгоритма

Для исследования возможностей параллелизма алгоритма ортогонализации Грама-Шмидта была написана собственная реализация [3] с использованием технологии MPI. В данной реализации задачи вычисления векторов [math]b_{j}[/math] равномерно распределяются по всем доступным вычислительным узлам. Как только на одном из узлов будет полностью вычислен некоторый [math]b_{j}[/math], происходит рассылка результата вычисления на все остальные узлы.

Тестирование данной реализации производилось на суперкомпьютере "Ломоносов" Суперкомпьютерного комплекса МГУ им. Ломоносова.

Технические подробности
Компилятор: openmpi/1.8.4-gcc Планировщик задач: slurm/2.5.6 Очереди: test, regular4 Команда постановки скрипта в очередь: sbatch -n <CPUS> --time=20 ompi a.out Тестовые данные (матрицы различной размерности) были сгенерированы с помощью скрипта Gram_Schmidt_process/scripts/matrixGenerator.py из репозитория [4]. Генерировались случайные квадратные матрицы выбранной размерности.

2.7 Существующие реализации алгоритма

Пример реализации базового алгоритма на языке Си с использованием технологий OpenMP и MPI представлен в статье .

Во всех библиотеках предназначенных для математических вычислений реализованы алгоритмы ортогонализации. В наиболее популярных:

[math]{\color{Blue}\bullet} \quad [/math] Mathematica - Orthogonalize[{v1,v2,…}] [5]

[math]{\color{Blue}\bullet} \quad [/math] Maxima - gramschmidt(x) [6]

[math]{\color{Blue}\bullet} \quad [/math] MatLab - orth(A) [7].