Участник:AleksLevin/Алгоритм Ланцоша вычисления собственных значений симметричной матрицы для точной арифметики (без переортогонализации)

Эта работа успешно выполнена Преподавателю: в основное пространство, в подстраницу Данное задание было проверено и зачтено. Проверено Konshin и ASA.

Основные авторы описания: Левин А.Д.

Алгоритм Ланцоша для точной арифметики (без переортогонализации)
Последовательный алгоритм
Последовательная сложность	[math]O(k\,n^2)[/math]
Объём входных данных	[math]\frac{n^2+3n}{2} + 1[/math]
Объём выходных данных	[math]k\;(n + 1)[/math]
Параллельный алгоритм
Высота ярусно-параллельной формы	[math]O(k\log_2 n)[/math]
Ширина ярусно-параллельной формы	[math]O(n^2)[/math]

1 Свойства и структура алгоритмов

1.1 Общее описание алгоритма

Данный алгоритм появился в 1950 г. и носит имя венгерского физика и математика Корнелия Ланцоша (венг. Lánczos Kornél). Алгоритм Ланцоша относится к итерационным методам вычисления собственных значений для матриц столь больших порядков [math] n[/math], что к ним нельзя применить прямые методы из-за ограничений по времени и памяти.

Сам Ланцош указывал, что его метод предназначен для отыскания нескольких собственных векторов симметричных матриц, хотя к методу сразу было обращено внимание, как к способу приведения всей матрицы к трёхдиагональному виду. Двадцатью годами позже канадский математик Крис Пэж показал, что, несмотря на чувствительность к округлениям, алгоритм Ланцоша - эффективное средство вычисления некоторых [math]k[/math] собственных чисел и соответствующих им собственных векторов. Обычно число [math]k[/math] берут в два раза больше, чем количество собственных значений матрицы, которые поставлена цель найти, и оно имеет порядок не более [math]10^2[/math].

Алгоритм Ланцоша для вычисления собственных значений симметричной матрицы [math]A[/math] соединяет в себе метод Ланцоша для построения последовательности подпространств Крылова и ортонормированных векторов Ланцоша и процедуру Рэлея-Ритца получения оптимальных приближений собственных значений и соответствующих собственных векторов исходной матрицы [math]A[/math].

В данной статье рассматривается вариант алгоритма Ланцоша, в котором опущено влияние ошибок округления на вычислительный процесс, хотя на практике этому посвящается отдельное внимание и существуют различные методы решения данной проблемы, такие как частичная или полная переортогонализация. Этим модифицированным методам посвящены отдельные статьи на данном ресурсе.

1.2 Математическое описание алгоритма

Обозначения и формулы, используемые в данном разделе, взяты из литературы, указанной по ссылке.

Алгоритм Ланцоша для вычисления [math]k[/math] собственных значений и собственных векторов вещественной симметричной матрицы [math]A=A^T[/math] в точной арифметике:

[math] \begin{align} q_1 = & \,\frac{b}{\|b\|_2},\; \beta_0 = 0,\; q_0 = 0\\ \mathbf{for} \; & j = 1 \; to \; k \,\; \mathbf{do} \\ & z = A\,q_j\\ & \alpha_j = q^T_j z\\ & z = z - \alpha_j q_j - \beta_{j-1}q_{j-1}\\ & \beta_j = \|z\|_2\\ & \mathbf{If} \; (\beta_j == 0) \; \mathbf{then}\; stop\; the\; algorithm \\ & \; q_{j+1} = \frac{z}{\beta_j} \\ & compute\; eigenvalues\; and \;eigenvectors\;of \;matrix \;\;T_j= Q^T_j A Q\;\;and\;estimate \;the\; errors\\ \mathbf{end} \; & \mathbf{for} \end{align} [/math]

В продемонстрированном выше алгоритме [math]b[/math] - заданный вещественный вектор. Также полагается известным алгоритм вычисления произведения матрицы [math]A[/math] на вектор [math]x[/math]. Введём матрицу Крылова, определяемую следующим соотношением: [math]K_j = [b,Ab,A^2b,...,A^{j-1}b][/math].

Далее, на практике, матрица [math]K[/math] заменяется матрицей [math]Q[/math], такой, что при любом числе [math]k[/math] линейные оболочки первых [math]k[/math] столбцов в [math]K[/math] и [math]Q[/math] являются одним и тем же подпространством. Тогда матрица [math]Q[/math], в отличие от матрицы [math]K[/math], хорошо обусловлена и легко обратима. В результате получаем матрицу [math]Q_j = [q_1, q_2, \dots, q_j][/math] размерности [math]n\times j[/math], столбцы которой ортогональны, являются базисом подпространства Крылова и называются векторами Ланцоша.

В алгоритме Ланцоша вычислению подлежит столько первых столбцов в матрице [math]Q_j[/math], сколько необходимо для получения требуемого приближения к решению [math]A\,x\,=b\,\,(A\,x=\lambda \, x)[/math].

Получение нулевого [math]\beta_j[/math] в итерационном процессе - событие, желательное в том смысле, что оно свидетельствует о том, что найдено некоторое подпространство, являющееся в точности инвариантным, а все собственные значения матрицы [math]T_j[/math] являются собственными значениями матрицы [math]A[/math]. На практике же нулевое и близкие к нулю значения получаются редко.

Затем на каждом шаге цикла формируется симметричная трёхдиагональная матрица [math]T_j = Q^T_j A Q[/math], к которой применяется процесс Рэлея-Ритца для поиска её собственных значений (на практике для поиска этих собственных значений можно использовать любой из специальных методов в параграфе книги по ссылке). Эти собственные значения, они же числа Ритца, и полагаются приближёнными собственными значениями исходной матрицы [math]A[/math].
Существует множество методов для отыскания собственных значений вещественной симметричной трехдиагональной матрицы. Большинство из них требует [math]O(n^2)[/math] операций , но существуют и быстрые алгоритмы, требующие лишь [math]O(n\ln n)[/math] операций.

Одним из возможных способов отыскать собственные значения симметричной трехдиагональной матрицы - прямое вычисление корней характеристического полинома [math]p_n(\lambda)[/math] через метод деления пополам, где формируется последовательность Штурма и локализуются собственные числа, являющиеся корнями характеристического полинома. Нахождение всех [math]n[/math] собственных значений матрицы этим способом требует [math]2n^2t[/math] умножений и вычитаний, где [math]t[/math] - число сделанных шагов с применением метода деления пополам. Соответствующие собственные вектора могут быть найдены посредством обратных итераций за [math] O(n) [/math] флопов.

На практике, если требуется только небольшая часть от всей совокупности собственных векторов и значений, и матрица имеет Хессенбергову или трёхдиагональную форму, очень эффективными будут методы факторизации, как, например, QR-алгоритм или QL-алгоритм со сдвигами (c целью ускорить алгоритм и сделать порядок сходимости квадратичным) или же без них.
Весьма молодые и не менее актуальные конкуренты QR и QL алгоритмов, применяющиеся для поиска собственных значений:

• Методы divide-and-conquer (разделяй и властвуй), появившиеся в 1980-ых годах
• Relatively robust representation методы, появившиеся в 1990-ых и позволяющие найти собственные числа симметричной матрицы порядка [math]n[/math] за [math]O(n^2)[/math] операций

Если требуется вычислить собственные векторы, то необходимо хранить вычисляемые векторы Ланцоша. Если работа при этом производится только с оперативной памятью, то при большом порядке исходной матрицы (а именно для таких матриц и предназначен метод Ланцоша) число шагов [math]j[/math], которые могут быть выполнены до того момента, как оперативная память будет исчерпана, будет очень незначительно, а следовательно, искомые собственные пары могут не успеть сойтись с требуемой точностью. В этом случае метод Ланцоша можно использовать итерационным образом: после выполнения заданного числа шагов процесс прерывается и, если еще не все требуемые пары Ритца сошлись с требуемой точностью, то формируется новый начальный вектор [math]q_1[/math], являющийся линейной комбинацией векторов Ритца, еще не сошедшихся с заданной точностью, и процесс начинается заново.

1.3 Вычислительное ядро алгоритма

Вычислительное ядро рассматриваемого алгоритма (наиболее ресурсно-затратная часть алгоритма) - формирование на каждом шаге цикла промежуточного вектора [math]z[/math], вычисляемого по формуле: [math]z = A\,q_j[/math]. Данная операция, по сравнению с другими операциями алгоритма, затратна и требовательна, как с точки зрения количества производимых операций, так и с точки зрения объема оперируемых данных.

Например, умножение матрицы размера [math]n\times n[/math] на вектор длины [math]n[/math] требует: [math]n^2+(n-1)n = 2n^2-n[/math] операций умножения и сложения. В свою очередь аналогичная операция умножения матрицы [math](n+1)\times (n+1)[/math] на вектор длины [math](n+1)[/math] требует: [math]2n^2+3n+1[/math] операций умножения и сложения. То есть повышение размерности задачи всего на 1 увеличивает число необходимых действий в этом шаге алгоритма на: [math]4n+1[/math].

Так же, стоит помнить, что, согласно разделу 1.2, данную операцию умножения матрицы на вектор необходимо выполнить [math]k[/math] раз. Нетрудно понять, насколько возрастает и колоссален масштаб операций, если в задачах, где критична точность, размерности [math]n[/math] могут иметь порядок [math]10^5[/math] или даже более.

1.4 Макроструктура алгоритма

Как уже было упомянуто в данной статье в описании алгоритма, рассматриваемый алгоритм состоит из двух последовательно выполненных алгоритмов: метод Ланцоша для построения последовательности подпространств Крылова и ортонормированных векторов Ланцоша и процедура Рэлея-Ритца получения оптимальных приближений собственных значений и соответствующих собственных векторов исходной матрицы.

В первой части алгоритма, где итерационно строятся Крыловское подпространство и трёхдиагональная матрица [math]T_j[/math], можно выделить следующие макрооперации:

• умножение матрицы на вектор (в свою очередь представляет собой умножение вектора на число и сложение векторов);
• вычисление нормы (скалярное произведение векторов + вычисление квадратного корня);
• скалярное произведение векторов;
• сложение векторов и их умножение на вещественные числа

Умножение матрицы на вектор - весьма дешевая и нетривиальная операция, если предполагать, что исходная матрица [math]A[/math] разреженная. Именно она подлежит оптимизации с использованием техник распараллеливания, поскольку она является вычислительным ядром алгоритма, а весь упомянутый процесс построения матрицы [math]T_j[/math] выполняется последовательно.

Рассмотрим вторую часть алгоритма - поиск собственных значений сформированной матрицы [math]T_j[/math].
Далее, наглядно, в виде псевдокода, представлен, упомянутый в разделе 1.2, QR-алгоритм (аналогично можно рассмотреть и QL-алгоритм) со сдвигами Релэя, который весьма популярен на практике.

[math] \begin{align} \mathbf{Input}: \;&tridiagonal\;\;matrix \;T\;with\;\;n\times n\;\;size\\ T^{(0)}&:=T\\ \mathbf{for}& \;\;m=n,...,2 \;\; \mathbf{do}\\ &k=0\\ & \mathbf{repeat}\\ & \quad \;\; k=k+1\\ & \quad \;\; \mu^{(k)}=T_{m,m}^{(k-1)}\\ & \quad \;\; Q^{(k)}R^{(k)}=T^{(k-1)}-\mu^{(k)}I\;\;using\;\;QR\;decomposition\\ & \quad \;\; T^{(k)}=R^{(k)}Q^{(k)}+\mu^{(k)}I\\ & \mathbf{until} \;\;\; |T_{m,m-1}^{(k)}| \;is\;\;small\;\;enough\\ & Save \;\;T_{m,m}^{(k)} \;\;as\;\; converged\;\;eigenvalue\;of\;T\\ & Remove \;\boldsymbol{n}\,th\;row\;and\;\boldsymbol{n}\,th\;column\;\;from \;T \\ & and\;take\;this\;new\;cropped\;matrix\;as\;new\;T^{(0)}\;with\;\;(n-1)\times (n-1)\;\;size\\ \mathbf{end}&\; \mathbf{for} \end{align} [/math]
Малость наддиагональных и поддиагональных элементов матрицы (фраза "small enough" в псевдокоде) подразумевает: [math] |T_{m,m-1}^{(k)}| \leq \varepsilon\,|T_{m,m}^{(k)}| \quad\quad [/math] , где [math] \varepsilon [/math] - заданная точность
Также вместо сдвига Релэя, обозначенного в алгоритме через [math]\mu^{(k)}[/math], часто на практике используется сдвиг по Уилкинсону, который даёт гарантированную сходимость внедиагональных элементов матрицы [math] T^{(k)} [/math], формируемой на каждом шаге, к нулю, при этом жертвуя монотонностью их убывания.
Подробнее с различными сдвигами и соответствующими оценками скоростей и количествами операций можно ознакомиться по указанной ссылке:.

Для совершения QR-декомпозиции на каждом шаге может использоваться любой из алгоритмов по ссылке. Подробные описания этих алгоритмов также доступны на данном ресурсе algowiki-project.
Так как мы оперируем не обычной матрицей и даже не Хессенберговой, а симметричной и трёхдиагональной, то скорость таких алгоритмов значительно возрастёт. Например, согласно данному ресурсу , для QL-алгоритма с неявными сдвигами:
Для трёхдиагональной матрицы объем арифметических действий составляет [math] O(n)[/math] на одну итерацию вместо [math] O(n^3)[/math] для матрицы общего вида, а число итераций для нахождения первых собственных значений примерно равно 4 - 5. Но на этих итерациях также уменьшаются внедиагональные элементы правого нижнего угла. И, таким образом, дальнейшие собственные значения ищутся значительно быстрее. Среднее число итераций на каждое собственное значение обычно составляет 1.3 - 1.6.
Аналогично QL, QR-разложение трёхдиагольной матрицы также требует [math] O(n)[/math] флопов

Подводя итог, во второй части алгоритма Ланцоша можно выделить следующие макрооперации:

• умножение матрицы на вещественное число;
• перемножение матриц;
• умножение и сравнение вещественных чисел;
• + набор других макроопераций в зависимости от выбора метода, с помощью которого будет совершаться сама QR или QL-декомпозиция (выше продемонстрированы, уже, как минимум, 3 разных способа).

Так же, важно заметить, что набор макропераций может быть несколько другим, если выбрать какой-либо иной современный метод поиска собственных чисел трёхдиагональной матрицы, не использующий QR и QL разложения(факторизацию). Два таких метода были упомянуты в пункте 1.2.

1.5 Схема реализации последовательного алгоритма

С целью полностью не дублировать раздел 1.2 данной статьи, где представлен наглядный и доступный для понимания псевдокод алгоритма, постараемся лишь коротко просуммировать и обобщить весь перечень последовательных действий в рассматриваемом алгоритме.

В качестве входных данных имеем: вещественная симметричная матрица [math]A[/math] размера [math]n\times n[/math], известный вещественный вектор [math]b[/math] длины [math]n[/math] и число [math]k\lt n[/math].

Далее:

• Инициализируем вещественную константу [math]\beta_0[/math] и векторы [math]q_0[/math] и [math]q_1[/math]
• Итерационно для всех [math]j=1,...,k[/math]:
  • Вычисляем вспомогательный вектор [math]z[/math], используя умножение матрицы на вектор
  • Вычисляем, используя скалярное произведение векторов, значение [math]\alpha_j[/math] - элемент на главной диагонали трёхдиагональной матрицы [math]T_j[/math]
  • Вычисляем по формуле новое значение и перезаписываем вектор [math]z[/math]
  • Вычисляем значение [math]\beta_j[/math] - элементы непосредственно над и под главной диагональю той же матрицы [math]T_j[/math]
  • Вычисляем, зная вектор [math]z[/math], очередной столбец матрицы [math]Q[/math], он же вектор Ланцоша : [math]\,\,q_{j+1}[/math]
  • Теперь, когда матрица [math]T_j[/math] сформирована на очередном шаге, находим её собственные значения и вектора любым доступным способом, о чём было подробно сказано в пункте 1.2
  • Переходим на следующую итерацию: [math]j[/math]++

1.6 Последовательная сложность алгоритма

Оценим количество операций и сложность последовательного алгоритма, изложенного в предыдущем разделе.

• Для вычисления вектора [math]z[/math] умножается матрица размера [math]n\times n[/math] на вектор длины [math]n[/math], и потребуется [math]n^2[/math] операций умножения и [math]n^2[/math] операций сложения.
• Умножение векторов [math]q^T_j[/math] и [math]z[/math] длины [math]n[/math] потребует [math]n[/math] операций умножения и [math]n[/math] операций сложения.
• При вычислении нового значения вектора [math]z[/math] поэлементное сложение двух векторов длины [math]n[/math] требует [math]n[/math] операций сложения.
• Умножение вектора длины [math]n[/math] на вещественное число требует [math]n[/math] операций умножения.
• Нахождение квадратичной нормы вектора [math]z[/math] длины [math]n[/math] требует [math]n[/math] умножений и [math]n[/math] сложений и ещё 1 операцию извлечения квадратного корня.
• Заключительное нахождение собственных значений и собственных векторов трёхдиагональной матрицы [math]T_j[/math] размера [math]j\times j[/math] с помощью QR-алгоритма потребует в худшем случае [math]O(j^3)[/math] операций.

Посчитаем теперь суммарное количество простейших операций на одной итерации алгоритма (без учёта записей в память):

• [math]n^2+5\,n[/math] операций умножения/деления
• [math]n^2+4\,n[/math] операций сложения/вычитания
• 1 операция извлечения квадратного корня
  

Отдельно после всех итераций при [math]j=k[/math] :

• [math]O(k^3)[/math] операций для поиска собственных значений и собственных векторов трёхдиагональной матрицы [math]T_k[/math]

Итого можно утверждать следующее:

Последовательная сложность одной итерации рассматриваемого алгоритма: [math]O(n ^ 2) [/math]
Суммарная сложность алгоритма ([math]k[/math] итераций): [math]O(k\,n ^ 2) + O(k ^ 3)[/math]

На практике же обычно рассматривается число [math]k\lt \lt n[/math], поэтому второе слагаемое можно опустить.

1.7 Информационный граф

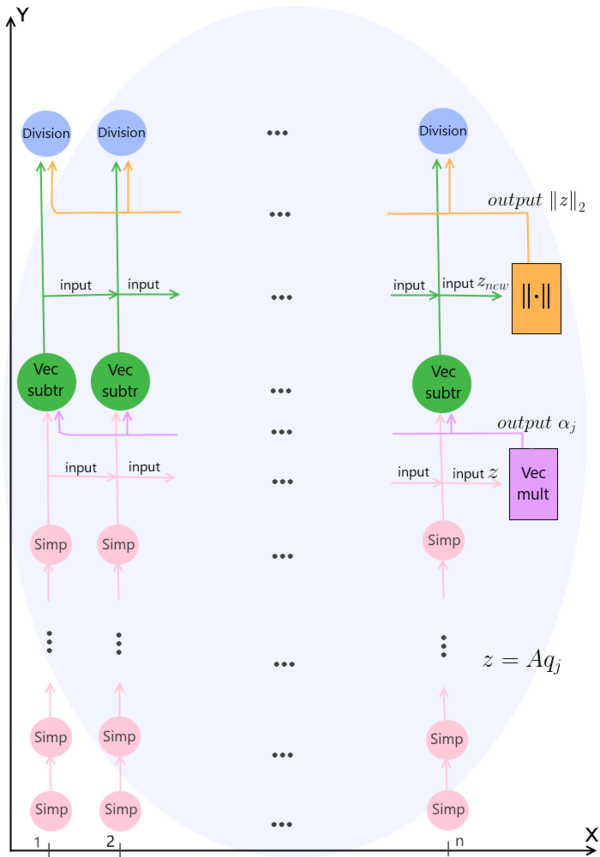
На рис. 1 продемонстрирован граф одной итерации (при каком-либо произвольном значении итератора [math]j[/math]) описанного алгоритма без отображения входных и выходных данных. Наглядно продемонстрированы связи между всеми действиями, и с помощью деления на [math]n[/math] потоков показано, какие операции возможно выполнять параллельно на каждом шаге с целью оптимизации и экономии машинного времени. В результате, после параллельно выполненных операций Division на заключительном ярусе, на выходе имеем значение следующего вектора Ланцоша [math]q_{j+1}[/math], после чего следует переход на следующую итерацию, и процесс повторяется.

Рис. 1 Структура одной итерации алгоритма

Обозначения на рисунке:
Simp (от англ. simple) - операции сложения и умножения вещественных чисел при вычислении произведения матрицы на вектор;

Vec mult (от англ. vectors multiplication) - операция скалярного умножения двух векторов;

Vec subtr (от англ. vectors subtraction, из-за использованных в операции вычитаний векторов) - операция умножения вектора на число (выполняется дважды) и формирование нового значения [math]z_{new}[/math] по формуле: [math]z_{new} = z - \alpha_j q_j - \beta_{j-1}q_{j-1} \;[/math];

[math]||\cdot||[/math] - операция вычисления нормы вектора;

Division - операция деления вектора на вещественное число [math]\beta_j[/math]

Важно отметить, что упомянутые выше операции также легко поддаются оптимизации. Например, попарные умножения вещественных координат векторов при вычислении скалярного произведения также легко выполняются параллельно на [math]n[/math] потоках, а затем можно применить суммирование методом сдваивания, о котором сказано в следующем разделе. Умножение или деление вектора на вещественное число являющееся, по определению, умножением или делением всех его координат на это число тоже может быть выполнено эффективнее, если мы используем [math]n[/math] потоков, а не выполняем эти действия последовательно.

1.8 Ресурс параллелизма алгоритма

Параллельные операции возможны только внутри итераций, так как рассматриваемый алгоритм является итерационным, и сами итерации строго последовательны.
Рассмотрим в этом разделе подробнее, какой выигрыш мы можем получить при распараллеливании операций внутри одной итерации согласно графу из предыдущего раздела.

Умножение вещественной симметричной матрицы [math]A[/math] размера [math]n\times n[/math] на вектор [math]b[/math] длины [math]n[/math] требует последовательного выполнения [math]n[/math] ярусов умножений и сложений. Сложение элементов вектора длины [math]n[/math] на каждом шаге перемножения можно оптимизировать и выполнить за [math]\log_2 n[/math] действий, если применять метод сдваивания.

Дальнейшие операции выполняются последовательно, а вычисление значений векторов происходит за один ярус операций сложения или умножения.

Ресурс параллелизма алгоритма вычисления собственных значений построенной трёхдиагональной матрицы [math]T_k[/math] размера [math]k\times k[/math] зависит от выбранного алгоритма (об этих алгоритмах подробнее было сказано в разделах 1.2 и 1.4). Будет очень затратно с точки зрения объёма материала пытаться рассмотреть пусть даже часть этих методов в этой статье, а так же тонкости их распараллеливания. Предлагаем читателям при желании самим ознакомиться с этими алгоритмами на данном ресурсе или прибегнув к иным источникам.

При классификации по высоте ЯПФ, таким образом, алгоритм Ланцоша без переортогонализации относится к алгоритмам с логарифмической сложностью, и его сложность равна [math]O(\log_2 n)[/math] с важным замечанием, что это сложность только одной итерации, а максимум в алгоритме может быть выполнено последовательно [math]k[/math] таких однотипных итераций, если не будет осуществлён ранний выход из цикла.

Несмотря на то, что на графе в предыдущем разделе для лучшей визуализации и понимания было изображено [math]n[/math] потоков (никаких допущений мы не делали и нарушений с точки зрения логики и математики нет, можно изобразить большее число потоков, просто часть времени некоторые из них могут бездействовать и не использоваться), на самом деле правильным и разумным будет реализовать начальное параллельное выполнение [math]n^2[/math] операций умножения всех вещественных элементов матрицы [math]A[/math] на соответствующие элементы вектора [math]q_j[/math], после чего применять тот же самый упомянутый метод сдваивания.

Поэтому при классификации по ширине ЯПФ его сложность будет квадратичной и равна [math]O(n^2)[/math].

1.9 Входные и выходные данные алгоритма

Входные данные алгоритма: вещественная симметричная [math]A[/math] размера [math]n\times n[/math], вещественный вектор [math]b[/math] длины [math]n[/math], и одно целое число [math]k[/math], означающее количество итераций.

Объём входных данных: [math]n^2 +n + 1 [/math]. Если учесть, что матрица симметричная и достаточно для её однозначного определения задать элементы на главной диагонали и элементы над или под ней, то можно сократить объём входных данных с целью экономии памяти до: [math]\ \frac{n^2-n}{2}+n+n+1 =\frac{n^2+3n}{2} + 1[/math]

Выходные данные алгоритма: вектор собственных значений [math]\Theta^k[/math] длины [math]k[/math], матрица [math]S^k[/math] из соответствующих собственных векторов размера [math]n\times k[/math].

Объём выходных данных: [math]k\;(n + 1)[/math].

1.10 Свойства алгоритма

В данном разделе перечислены без какой-либо хронологии или связи друг с другом наиболее важные и разнообразные свойства алгоритма, на которые стоит и полезно обратить внимание, а также которые выгодно отличают его от схожих алгоритмов, решающих ту же задачу.
1) Отношение последовательной сложности алгоритма к параллельной,с учётом [math]k[/math] итераций, равно [math]\;\;\frac{kn^2}{k \log_2{n}}=\frac{n^2}{\log_2{n}}[/math];
2) Вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных, равна [math]\;\;\frac{k\,n^2}{0.5\,n^2+1.5\,n+k\,n+k+1}[/math] и [math]\approx 2\,k[/math], так как на практике верно отношение [math]k\lt \lt n[/math] ;

3) Для собственных значений формируемых матриц [math]T_j[/math] верно отношение (следствие теоремы Коши о перемежаемости): [math]\lambda_i(T_{k+1})\geq \lambda_i(T_{k})\geq \lambda_{i+1}(T_{k+1})\geq \lambda_{i+1}(T_{k})[/math] ;

4) Крайние (наибольшие и наименьшие) собственные значения матриц [math]T_j[/math] сходятся к крайним собственным значениям матрицы [math]A[/math] первыми (это часто происходит уже на ранних шагах при [math]j\approx 2\,\sqrt{n}[/math]), а собственные значения в середине спектра - последними;

5) Из-за ограниченной точности постепенно теряется ортогональность вектора Ланцоша [math]q_j[/math] к предыдущим векторам Ланцоша, поэтому необходимо примерно каждые 10-15 итераций проводить дорогостоящую операцию реортогонализации, но это уже будет иной алгоритм с очень малым различием в одной операции и в программном коде, реализующем его, соответственно;

6) Эффективность и быстрота выполнения алгоритма очень сильно зависит от скорости памяти (диска). Согласно тесту только 6% времени работы программы приходится на вычисления, остальное время затрачивается на ожидание отклика диска;

7) Метод Ланцоша удобен тем, что не требует хранения исходной матрицы полным массивом: метод использует исходную матрицу только в операциях умножения матрицы на вектор, что позволяет эффективно использовать разреженность матрицы или регулярность структуры матрицы. Поэтому метод Ланцоша может быть использован для матриц таких больших порядков, когда методы вращений и отражений не могут быть применены.

2 Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

Для исследования масштабируемости рассматриваемого алгоритма Ланцоша без переортогонализации автором была реализована программа на языке С++ с использованием технологии MPI. Дальнейшее исследование было проведено на суперкомпьютере "Ломоносов" Суперкомпьютерного комплекса МГУ.
Важно отметить, что реализованная программа выполняет только первую часть алгоритма - формирование трёхдиагональной матрицы [math]T_j[/math]. Вторая часть алгоритма (задача поиска собственных значений матрицы [math]T_j[/math]) может быть решена несколькими методами, каждый из которых обладает своей эффективностью распараллеливания и характерными свойствами. Подробно этот вопрос уже обсуждался в статье ранее, поэтому не будем ещё раз заострять на этом внимание и останавливаться.

Сборка осуществлялась со следующими параметрами:

• Компилятор intel/15.0.090
• Openmpi/1.8.4-icc

В серии проведённых расчётов рассматривались следующие числовые значения параметров:

• Размер [math]n[/math] задачи и, соответственно, матрицы [math]A[/math], задействованной в операции умножения на вектор: [2000 : 30000] с шагом 1000
• Число [math]p[/math] процессоров: 1, 2, 4, 16, 32, 48, 64, 96, 128, 192, 256
• Число итераций в алгоритме: [math]k=350[/math]

Число [math]k[/math] взято таким вопреки информации в начале статьи, где говорится, что значение [math]k[/math] редко превышает [math]10^2[/math] (хоть мы и имеем право брать его любым по нашему усмотрению). Это сделано исключительно для лучшей визуализации пиков на графиках в данном разделе и наглядности получаемых результатов, так как при меньших на порядок значениях параметра [math]k[/math] времена выполнения программ были слишком малы даже при минимальных числах процессоров и максимальных размерах [math]n[/math] задачи.
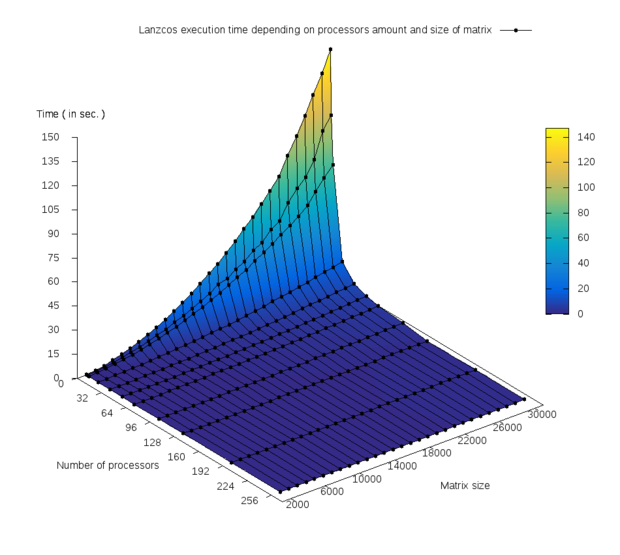
На рис. 2 изображён график зависимости времени выполнения программы от числа процессоров и размера [math]n[/math] задачи.

Рис. 2 График зависимости времени выполнения программы.

Рис. 3 График зависимости эффективности распараллеливания программы.

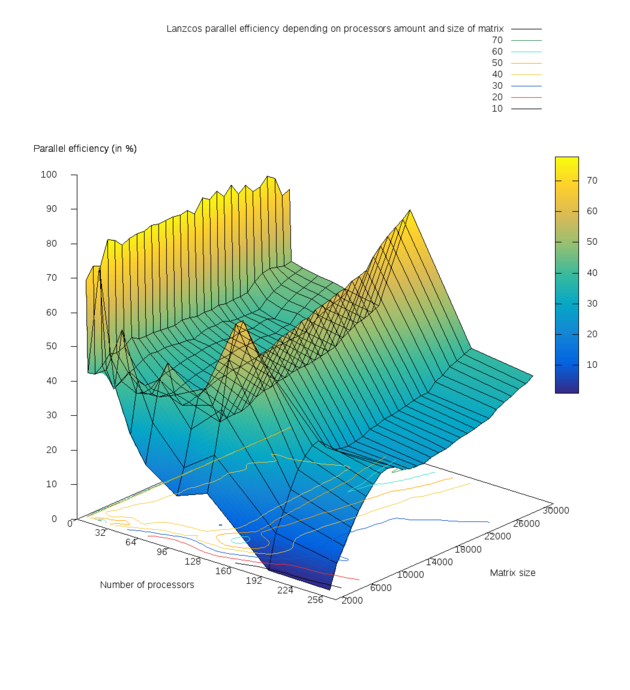
Многочисленные тесты показали при малых количествах ядер уменьшение времени выполнения программы почти в 2 раза при увеличении числа ядер в 2 раза на всём диапазоне размеров матриц, что и отражает сильный излом на первом графике. Изменение значений времени можно легко оценить по предоставленной цветовой шкале. Был построен график эффективности распараллеливания (parallel efficiency) в зависимости от числа процессоров и размера задачи, изображённый на рис. 3. Получены следующие результаты численных экспериментов:

• Средняя эффективность распараллеливания программы составила: 42.5576% ;
• Минимальная эффективность реализации: 0.674% (число процессоров 256 и минимальный размер матрицы 2000);
• Максимальная эффективность реализации: 77.773% (число процессоров 2, размер матрицы 20000).

Нужно понимать, что это лишь экстремумы, соответствующие двум экспериментам, которые сами по себе не дают полной картины и не позволяют однозначно судить о параллельных качествах алгоритма и реализующей его программы при столь большом числе параметров и проводимых расчётов.
На основании рис. 3 можно отметить следующие значимые и важные факты:

• Имеется ярко выраженный спад эффективности при минимальном рассматриваемом размере матрицы [math]n=2000[/math] вдоль всей оси OY, отвечающей за число процессоров;
• Присутствуют два пика эффективности (жёлтого цвета на рис. 3): при числе [math]p[/math] процессоров 2 и 128. Затем при дальнейшем увеличении числа процессоров с 128 до 256 наблюдается постепенное уменьшение эффективности реализации. Это связано с увеличением накладных расходов и затрат времени на обмены сообщениями между процессами.

2.7 Существующие реализации алгоритма

Несмотря на то, что алгоритм является далеко не самым популярным, алгоритмом, про который нельзя сказать, что он всегда «на слуху», на сегодняшний день существует множество реализаций на различных популярных языках.
Перечислим далее некоторые из них, указывая язык программирования, лежащий в их основе, и некоторые важные характеристики, которые обсуждались в статье ранее:

• Code on netlib.org by Jane Cullum and Ralph Willoughby (Fortran 77; без реортогонализации векторов; без реализации распараллеливания)
• Lanczos algorithm on freesourcecode.net (Matlab; присутствует реортогонализация векторов; без реализации распараллеливания)
• Lanczos for eigenvalues in Numerical Linear Algebra, Spring 2007 (Matlab; частичная или полная реортогонализация - доступны оба варианта; без реализации распараллеливания)
• Planso (название происходит от parallel Lanso.f) code by Kesheng Wu and Horst D. Simon (Fortran 77; частичная реортогонализация векторов; использование MPI для коммуникаций)
• Lanczos.cpp in the Vienna Computing Library (C++, частичная реортогонализация, без реализации распараллеливания)
• Parallel Eigen Values code using C++ AMP on microsoft msdn blog (C++; ? ; распараллеливание есть и реализовано через C++ AMP)