Участник:Stanis-morozov/Алгоритм Тренча вычисления спектра симметрической теплицевой матрицы

Задача нахождения собственных значений и собственных векторов для матрицы [math]A[/math] заключается в поиске таких соответствующих друг другу чисел [math]\lambda[/math] и ненулевых векторов [math]x[/math], которые удовлетворяют уравнению [math]Ax=\lambda x[/math]. Числа [math]\lambda[/math] называются собственными значениями, а вектора [math]x[/math] - соответствующими им собственными векторами

Теплицевой матрицей называется матрица, в которой на всех диагоналях, параллельных главной, стоят равные элементы.

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Задача эффективного вычисления собственных значений матриц является одной из основных задач линейной алгебры. Известно, что собственные значения произвольной матрицы невозможно вычислить за конечное число операций, однако существует множество итерационных методов, позволяющих решать эту задачу, например, QR-алгоритм. Однако, для некоторых специальных классов матриц можно предложить более эффективные методы, чем QR-алгоритм. Так, в 1989 была опубликована работа В. Тренча , в которой был предложен метод вычисления собственных значений симметрической теплицевой матрицы, учитывающий особенности структуры таких матриц, и допускающий эффективную параллельную реализацию .

1.2 Математическое описание алгоритма

Пусть имеется матрица [math]T_{n}[/math] порядка [math]n\times n[/math] следующего вида:

[math] T_{n} = \begin{bmatrix} t_{0} & t_{1} & t_{2} & \cdots & t_{n-2} & t_{n-1} \\ t_{1} & t_{0} & t_{1}& \cdots & t_{n-3} & t_{n-2} \\ t_{2} & t_{1} & t_{0} & \cdots & t_{n-4} & t_{n-3} \\ \vdots & \vdots & \ddots & \ddots & \ddots & \vdots \\ t_{n-2} & \cdots & \cdots & t_{1} & t_{0} & t_{1} \\ t_{n-1} & \cdots & \cdots & t_{2} & t_{1} & t_{0} \\ \end{bmatrix} [/math]

Требуется найти ее собственные значения. Будем также предполагать, что ни одно из собственных значений [math]T_{n}[/math] не является собственным значением для [math]T_{1}, \dots, T_{n-1}[/math]. Однако, практические эксперименты, проведенные во многих работах, показывают, что данное ограничение существенно только в теории и не дает о себе знать в практических вычислениях.

Введем следующие обозначения. Обозначим

[math]p_{m}(\lambda) = det[T_{m} - \lambda I_{m}][/math]

[math]q_{m}(\lambda) = p_{m}(\lambda) / p_{m-1}(\lambda)[/math]

Метод Тренча состоит в нахождении корней рациональной функции [math]q_{n}(\lambda)[/math]. При сделанных предположениях относительно матрицы [math]T_{n}[/math], эта задача равносильна задаче нахождения собственных значений матрицы [math]T_{n}[/math].

Обозначим также [math] v_{m} = \begin{bmatrix} t_{1} \\ t_{2} \\ \vdots \\ t_{m} \\ \end{bmatrix} [/math]

Можно доказать, что если [math]\lambda[/math] не является собственным значением [math]T_{n}[/math], а [math]z_{m}(\lambda)[/math] является решением

[math](T_{m} - \lambda I_{m})z_{m}(\lambda) = v_{m}[/math],

то

[math]q_{m}(\lambda) = t_{0} - \lambda - v_{m-1}^{T} z_{m-1}(\lambda)[/math].

Для решения системы можно использовать следующий модифицированный алгоритм Левинсона-Дурбина, эквивалентный в данном случае построению [math]LDL^{T}[/math] разложения для матрицы [math]T_{m} - \lambda I_{m}[/math]. Вычисления алгоритма проходят по следующим формулам:

[math] q_{1}(\lambda) = t_{0} - \lambda \\ z_{1,1}(\lambda) = t_{1} / q_{1}(\lambda) \\ q_{m}(\lambda) = (1 - z_{m-1, m-1}^2(\lambda)) q_{m-1}(\lambda) \\ z_{m,m}(\lambda) = q_{m}^{-1}(\lambda)\big(t_{m} - \sum\limits_{j=1}^{m-1} t_{m-j}z_{j,m-1}(\lambda)\big) \\ z_{j,m}(\lambda) = z_{j,m-1}(\lambda) - z_{m,m}(\lambda)z_{m-j,m-1}(\lambda), 1 \le j \le m-1 [/math]

С другой стороны, заметив, что на диагонали матрицы [math]D[/math] в полученном [math]LDL^{T}[/math] разложении стоят значения [math]q_{j}(\lambda)[/math], и применяя закон инерции квадратичных форм получаем, что количество элементов [math]q_{j}(\lambda)[/math] меньших нуля, в точности равно количеству собственных значений матрицы [math]T_n[/math], меньших [math]\lambda[/math].

Кроме того, приведем важный для эффективного вычисления результат:

Теорема. Предположим, что [math]\alpha[/math] и [math]\beta[/math] не являются собственными значениями ни для какой из матриц [math]T_{1}, \dots, T_{n}[/math], и что [math](\alpha, \beta)[/math] содержит в точности одно собственное значение [math]T_{n}[/math] кратности единица. Тогда [math](\alpha, \beta)[/math] не содержит собственных значений матрицы [math]T_{n-1}[/math] тогда и только тогда, когда [math]q_{n}(\alpha) \gt 0[/math] и [math]q_{n}(\beta) \lt 0[/math].

Отсюда вытекает следующий алгоритм нахождения [math]j[/math]-го по величине собственного значения матрицы [math]T_{n}[/math].

1. Находим отрезок, внутри которого лежат все собственные значения матрицы. Например, его можно найти с помощью кругов Гершгорина.

2. Локализуем [math]j[/math]-ое собственное значение. Для этого используем метод деления отрезка пополам. Обозначим [math]neg_{n}(\lambda)[/math] количество собственных значений [math]T_{n}[/math] меньших [math]\lambda[/math]. Имея процедуру вычисления [math]neg_{n}(\lambda)[/math] и [math]q_{n}(\lambda)[/math] легко построить алгоритм, сходящийся к [math]\alpha[/math] и [math]\beta[/math], таким что

[math]neg_{n}(\alpha) = j - 1[/math] и [math]neg_{n}(\beta) = j[/math]

[math]q_{n}(\alpha) \gt 0[/math] и [math]q_{n}(\beta) \lt 0[/math]

3. Тогда на этом интервале функция [math]q_{n}(\lambda)[/math] будет непрерывна (и более того, бесконечно дифференцируема) и можно применять другие, более эффективные методы нахождения корня уравнения.

1.3 Вычислительное ядро алгоритма

Вычислительное ядро алгоритма состоит из двух частей. Первая часть состоит в локализации всех собственных значений, т.е. нахождении для каждого собственного значения матрицы [math]\lambda_j[/math] такого отрезка [math](a, b)[/math], что он содержит в себе [math]\lambda_j[/math] и не содержит других собственных значений матрицы, а также собственных значений матрицы меньшей размерности.

Вторая часть состоит в приближении локализованного на интервале собственного значения с заданной точностью.

1.4 Макроструктура алгоритма

Одна из базовых операций - нахождение интервала, содержащего все собственные значения матрицы с помощью кругов Гершгорина. На псевдокоде эта задача может быть реализована следующим образом (за t_j обозначен элемент теплицевой матрицы t_kl для которого k - l = j):

   mx = 0
   for i = 1, n:
       s1 = s2 = 0
       for j = 2, i:
           s1 += |tj|
       for j = 2, n - i:
           s2 += |tj|
       mx = max(mx, s1 + s2)
   a = t0 - mx
   b = t0 + mx

Вычисление величин [math]neg_n(\lambda)[/math] и [math]q_n(\lambda)[/math] происходит одновременно по следующим формулам:

   q1(λ) = t0 - λ
   z1,1(λ) = t1 / q1(λ)
   qm(λ) = (1 - z2m-1, m-1(λ)) qm-1(λ)
   tmp = 0
   for j = 1, m - 1:
       tmp += tm-jzj,m-1(λ)
   zm,m(λ) = q-1m(λ)(tm - tmp)
   for j = 1, m:
       zj,m(λ) = zj,m-1(λ) - zm,m(λ)zm-j,m-1(λ)
   negn(λ) = 0
   for j = 1, n:
       if qj(λ) < 0:
           negn(λ) += 1

1.5 Схема реализации последовательного алгоритма

1. Находим с помощью кругов Гершгорина интервал [math](a, b)[/math] на котором содержатся все собственные значения матрицы. Во избежание проблем с точным попаданием в собственные значения к [math]a[/math] и [math]b[/math] можно добавить случайные возмущения, расширяющие интервал.
2. Инициализируем очередь интервалов интервалом [math](a, b, 1, n)[/math], где [math]a[/math] и [math]b[/math] обозначают границы интервалов, а [math]1[/math] и [math]n[/math] номера собственных значений, которые на нем находятся.
3. Извлекаем интервал [math](l, r, p, q)[/math] из очереди
4. Если [math]p \ne q[/math], переходим к шагу 6
5. Вычисляем пары [math](neg_n(l), q_n(l))[/math] и [math](neg_n(r), q_n(r))[/math]. Если [math]neg_n(l) = p - 1[/math], [math]neg_n(r) = p[/math], [math]q_n(l) \gt 0[/math] и [math]q_n(r) \lt 0[/math], то добавляем интервал [math](l, r, p)[/math] в список локализованных интервалов и переходим к шагу 3
6. Вычисляем [math]\lambda = (l + r) / 2[/math] и [math]neg_n(\lambda)[/math]
7. Если [math]neg_n(\lambda) \le p - 1[/math], то добавляем интервал [math](\lambda, r, p, q)[/math] в очередь и переходим к шагу 3
8. Если [math]neg_n(\lambda) \ge q[/math], то добавляем интервал [math](l, \lambda, p, q)[/math] в очередь. Иначе добавляем в очередь [math](l, \lambda, p, neg_n(\lambda))[/math] и [math](\lambda, r, neg_n(\lambda) + 1, q)[/math].
9. Если очередь не пуста, переходим к шагу 3
10. Извлекаем интервал [math](l, r, j)[/math] из списка локализованных интервалов
11. Если [math]r - l \le \epsilon[/math] переходим к шагу 14
12. Вычисляем [math]\lambda = (l + r) / 2[/math] и [math]neg_n(\lambda)[/math]
13. Если [math]neg_n(\lambda) \le p - 1[/math], то [math]l = \lambda[/math], иначе [math]r = \lambda[/math]. Переходим к шагу 11
14. Запоминаем [math]j[/math]-ое собственное значение как [math](l + r) / 2[/math]. Если список локализованных интервалов не пуст, переходим к шагу 10.

1.6 Последовательная сложность алгоритма

Число операций, необходимых для вычисления спектра матрицы зависит от требуемой точности вычислений. Легко видеть, что число операций, необходимых для вычисления [math]neg_n(\lambda)[/math] и [math]q_n(\lambda)[/math] равно [math]O(N^2)[/math]. Вычисление начально интервала, содержащего все собственные значения также требует [math]O(N^2)[/math] операций. Также нетрудно понять, что число операций, необходимых для приближения локализованного собственного значения с заданной точностью равно [math]O(N^2\log \frac{M}{\epsilon})[/math], где [math]\epsilon[/math] - требуемая точность, а [math]M[/math] - величина исходного интервала ([math]O(N^2)[/math] на каждую итерацию и [math]\log \frac{M}{\epsilon}[/math] итераций). Теоретическая оценка числа итераций, необходимых для локализации одного собственного значения неизвестна, однако при достаточно высокой требуемой точности (такой, чтобы после локализации было необходимо дальнейшее приближение собственного значения), это число итераций, очевидно, меньше [math]\log \frac{M}{\epsilon}[/math]. Далее, так как необходимо вычислить каждое собственное значение, итоговое число операций равно [math]O(N^3\log \frac{M}{\epsilon})[/math], где [math]N[/math] - размерность матрицы, [math]\epsilon[/math] - требуемая точность приближения, а [math]M = \|T_n\|_{\infty}[/math]. Стоит заметить также, что алгоритм позволяет вычислять не весь спектр сразу, а лишь необходимые [math]k[/math] собственных значений. Тогда для этого потребуется [math]O(k N^2\log \frac{M}{\epsilon})[/math] операций.

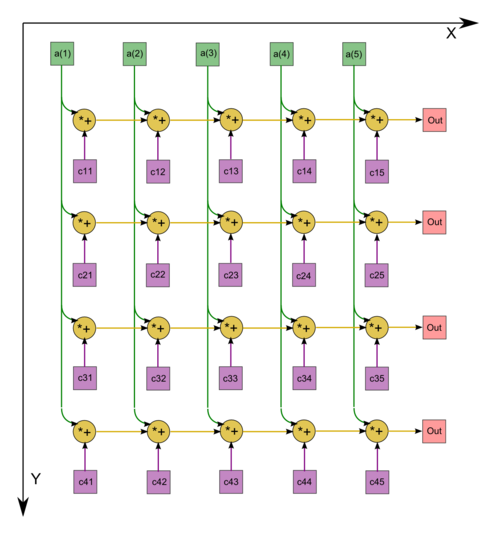
1.7 Информационный граф

Рисунок 1. Информационный граф вычисления собственных значений симметрической теплицевой матрицы

Опишем значения вершин информационного графа.

1. Вершина [math]T_n[/math] обозначает входные данные алгоритма - матрицу [math]T_n[/math]
2. Вершина [math]G[/math] обозначает вычисление интервала, содержащего все собственные значения с помощью кругов Гершгорина
3. Вершина [math]C[/math] обозначает условный переход при завершении локализации некоторого собственного значения, к его уточнению. Передача данных вниз в графе происходит только при срабатывании условия. Передача данных вправо происходит всегда
4. Вершина [math]P[/math] обозначает процесс дробления следующего интервала из очереди при локализации собственных значений
5. Вершина [math]F[/math] обозначает процесс уточнения локализованного собственного значения
6. Вершина [math]\lambda_j[/math] обозначает выходные данные алгоритма - вычисленное собственное значение

1.8 Ресурс параллелизма алгоритма

Глядя на последовательную версию алгоритма, становится ясно, что локализовывать собственные значения можно не в одной последовательной очереди, а разбив номера от [math]1[/math] до [math]n[/math] на [math]d[/math] равных частей (где [math]d[/math] - число доступных узлов) и инициализировать очередь лишь подотрезком на каждом узле. Также, приближения локализованных собственных значений можно производить независимо на каждом узле. Это означает полную распараллеливаемость алгоритма. Тогда число операций, необходимое для вычисления спектра равно [math]O\Big(\frac{N^3\log \frac{M}{\epsilon}}{d}\Big)[/math] при [math]d \lt N[/math]. При наличии бесконечного числа узлов, асимптотическая сложность будет равна [math]O(N^2\log \frac{M}{\epsilon})[/math].

1.9 Входные и выходные данные алгоритма

На вход алгоритму подается размер матрицы [math]n[/math] и симметрическая теплицева матрица [math]T_n[/math] размера [math]n \times n[/math]. Также предполагается, что ни одно из собственных значений [math]T_{n}[/math] не является собственным значением для [math]T_{1}, \dots, T_{n-1}[/math], однако утверждается, что это ограничение не затрудняет практического применения. Также на вход подается число [math]\epsilon \gt 0[/math] - требуемая абсолютная погрешность вычисления собственных значений.

Результатом работы алгоритма является массив из [math]n[/math] вещественных чисел, [math]j[/math]-ое из которых с точностью до [math]\epsilon[/math] равно [math]j[/math]-ому собственному значению матрицы [math]T_n[/math].

2 Программная реализация алгоритма

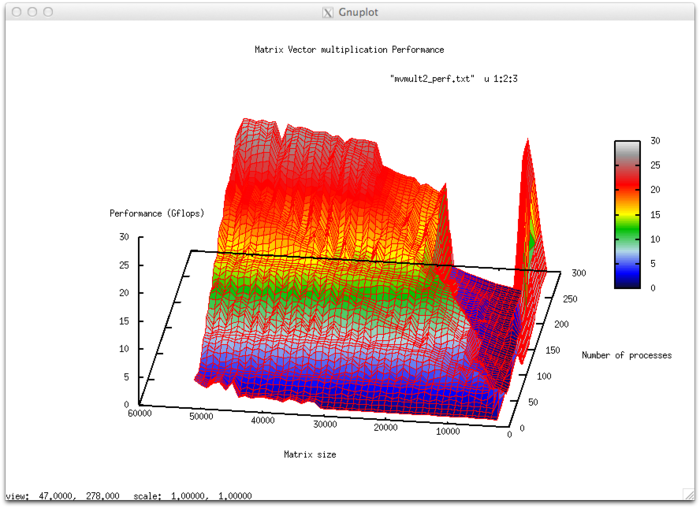
2.1 Масштабируемость алгоритма и его реализации

Исследование проводилось на суперкомпьютере "Ломоносов" Суперкомпьютерного комплекса Московского университета.

Набор и границы значений изменяемых параметров запуска реализации алгоритма:

число процессоров [2 : 200] с шагом 20; размер матрицы [100 : 1000] c шагом 100.

На следующем рисунке приведен график времени работы выбранной реализации алгоритма вычисления собственных значений симметрической теплицевой матрицы в зависимости от изменяемых параметров запуска.

Рисунок 2. Параллельная реализация алгоритма вычисления собственных значений симметрической теплицевой матрицы

2.2 Существующие реализации алгоритма

О существующих в популярных пакетах реализациях этого алгоритма ничего не известно в виду не очень широкого круга задач, которые он решает. Все существующие реализации создавались авторами исследований и не публиковались.