Участник:Y.ryabkova/Умножение матриц методом Штрассена
Основные авторы описания: Ю.В.Рябкова
Содержание
- 1 Свойства и структура алгоритмов
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритмов
1.1 Общее описание алгоритма
Алгоритм Штрассена, описанный в 1969 году Фолькером Штрассеном, предназначен для умножения двух произвольных матриц при условии согласованности их размеров. В данном варианте алгоритма будет рассмотрен только частный случай умножения квадратных матриц порядка [math]n[/math] над полем вещественных чисел [math]\mathbb{R}[/math].
В 1965 году Штрассен нашел способ умножения двух матриц размера [math]2 \times 2[/math] с использованием семи умножений[1], в то время как классический алгоритм перемножения матриц требует восьми умножений. Стоит отметить, что данный способ не использует свойство коммутативности для операции перемножения чисел.
Теперь предположим, что [math]n = 2^L[/math], [math] L \in \mathbb{N} [/math] (далее будет показано, что это предположение не нарушает общности рассуждений), и будем рассматривать матрицы [math]A[/math] и [math]B[/math] как блочные [math]2 \times 2[/math]-матрицы с размером блоков [math]\frac{n}{2} \times \frac{n}{2} [/math]. Так как для блочных матриц правила умножения остаются теми же, как если бы на месте блока стояло число, а в методе Штрассена умножения [math]2 \times 2[/math]-матриц не используется коммутативность, этот метод подходит и для умножения блочных [math]2 \times 2[/math]-матриц. Таким образом, от задачи умножения [math]2 \times 2[/math]-матриц с семью умножениями можно перейти к задаче умножения [math]n \times n[/math]-матриц, требующей не более чем [math] O(7n^{\log_27}) [/math] операций, что асимптотически лучше классического способа умножения матриц сложностью [math]O(n^3)[/math]. На данный момент известны и более быстрые методы умножения матриц, однако алгоритм Штрассена относительно прост в реализации и эффективен на плотных матрицах не очень больших размеров, поэтому всё ещё широко используется.
1.2 Математическое описание алгоритма
Пусть [math] A, B \in \mathbb{R}^{n \times n} [/math] — заданные плотные матрицы. Вычислим матрицу [math] C \in \mathbb{R}^{n \times n} [/math], такую, что [math] C = AB [/math].
Для удобства будем полагать, что [math] n = 2^L, L \in \mathbb{N} [/math]. Это предположение не ограничивает общности рассуждений, так как если это свойство не выполнено и [math] n \lt 2^L [/math], можно рассмотреть квадратные матрицы [math]\tilde{A}[/math] и [math]\tilde{B}[/math] порядка [math] 2^L [/math] следующего вида:
- [math] \tilde{A} = \begin{bmatrix} A & 0 \\ 0 & 0 \end{bmatrix}, \: \: \tilde{B} = \begin{bmatrix} B & 0 \\ 0 & 0 \end{bmatrix}, [/math]
то есть матрицы, полученные из матриц [math] A [/math] и [math] B [/math] дополнением их нулевыми строками и столбцами в позициях [math] i = \overline{n+1, 2^L} [/math] до размера [math] 2^L \times 2^L [/math]. По правилу перемножения блочных матриц:
- [math] \tilde{C} = \tilde{A}\tilde{B} = \begin{bmatrix} AB & 0 \\ 0 & 0 \end{bmatrix} = \begin{bmatrix} C & 0 \\ 0 & 0 \end{bmatrix}. [/math]
Таким образом, решая задачу для матриц [math] \tilde{A} [/math] и [math]\tilde{B} [/math], получим решение исходной задачи умножения матриц [math] A [/math] и [math] B [/math] как левый верхний [math]n \times n[/math]-блок матрицы [math]\tilde{C}[/math]. Аналогичным образом можно не ограничивая общности предположить, что [math] n = s \cdot 2^L, \: L, s \in \mathbb{N} [/math].
Итак, пусть [math] n = 2^L, L \in \mathbb{N} [/math]. Рассмотрим матрицы [math] A [/math] и [math] B [/math] как блочные [math] 2 \times 2 [/math]-матрицы с квадратными блоками порядка [math]\frac{n}{2}[/math]:
- [math] A = \begin{bmatrix} A_{11} & A_{12} \\ A_{21} & A_{22} \end{bmatrix}, \: \: B = \begin{bmatrix} B_{11} & B_{12} \\ B_{21} & B_{22} \end{bmatrix}. [/math]
Их произведение [math] C = AB [/math], согласно алгоритму Штрассена, вычисляется следующим образом:
- [math] \begin{align*} &S_{1} = A_{11} + A_{22}, & &T_{1} = B_{11} + B_{22}, \\ &S_{2} = A_{21} + A_{22}, & &T_{2} = B_{11}, \\ &S_{3} = A_{11}, & &T_{3} = B_{12} − B_{22}, \\ &S_{4} = A_{22}, & &T_{4} = B_{21} − B_{11}, \\ &S_{5} = A_{11} + A_{12}, & &T_{5} = B_{22}, \\ &S_{6} = A_{21} − A_{11}, & &T_{6} = B_{11} + B_{12}, \\ &S_{7} = A_{12} − A_{22}, & &T_{7} = B_{21} + B_{22}, \end{align*} [/math]
- [math] \alpha_{i} = S_{i} \cdot T_{i}, \: i = \overline{1,7}, [/math]
- [math] C_{11} = \alpha_{1} + \alpha_{4} - \alpha_{5} + \alpha_{7}, [/math]
- [math] C_{12} = \alpha_{3} + \alpha_{5}, [/math]
- [math] C_{21} = \alpha_{2} + \alpha_{4}, [/math]
- [math] C_{22} = \alpha_{1} + \alpha_{3} - \alpha_{2} + \alpha_{6}, [/math]
- [math] C = \begin{bmatrix} C_{11} & C_{12} \\ C_{21} & C_{22} \end{bmatrix}.[/math]
Для вычисления матриц [math] \alpha_{i}, i = \overline{1,7} [/math], также требуется выполнить семь матричных умножений по формулам, данным выше, но уже для матриц порядка [math] \frac{n}{2} [/math]. Таким образом, получаем рекурсивный алгоритм, на каждом шаге рекурсии требующий семи умножений и сводящий задачу размера [math]k[/math] к задаче размера [math]\frac{k}{2}[/math]. Всего потребуется [math]\log_{2}n[/math] рекурсивных шагов, на последнем из которых задача будет сведена к перемножению двух чисел. Однако, на практике разумно продолжать рекурсивный процесс до тех пор, пока [math]k[/math] не станет достаточно малым (или, в случае [math] n = s \cdot 2^L [/math], пока [math]k[/math] кратно 2), а далее использовать классический способ умножения матриц. Именно такой вариант метода рассматривается в данном описании. Это связано с тем, что на малых матрицах алгоритм Штрассена теряет эффективность в сравнении с классическим алгоритмом умножения матриц, так как требует большого числа сложений.
Итак, пусть весь процесс перемножения матриц требует [math] m+1 [/math] рекурсивных шагов, где первые [math] m [/math] шагов выполняются в соответствии с алгоритмом Штрассена, а на последнем шаге используется классический алгоритм умножения матриц.
1.3 Вычислительное ядро алгоритма
В описанном алгоритме можно выделить два вычислительных ядра: первое соответствует операциям, выполняемым на первых [math] m [/math] рекурсивных шагах, а второе - последнему рекурсивному шагу с номером [math] m + 1[/math].
Вычислительное ядро последовательного варианта алгоритма Штрассена на каждом рекурсивном шаге, кроме последнего, можно составить из вычисления матриц [math] S_{i}, T_{i}, \: i = \overline{1, 7} [/math], и блоков матрицы [math] C [/math] из матриц [math] \alpha_{i}, \: i = \overline{1, 7} [/math] по формулам, данным в математическом описании алгоритма. Все эти вычисления представляют из себя сложения (вычитания) матриц порядка [math] k [/math], зависящего от номера шага [math] s_m [/math] следующим образом: [math] k = \frac{n}{2^{s_m}} [/math]. Операции выполняются поэлементно. Таким образом, первое вычислительное ядро алгоритма сводится к операциям сложения (вычитания) чисел на каждом рекурсивном шаге.
Вычислительное ядро алгоритма на последнем, [math] m+1 [/math]-ом рекурсивном шаге, состоит из операций перемножения двух матриц по классическому алгоритму кубической сложности, основную часть которого составляют умножения чисел.
Указанные операции составляют основную часть метода, причем с увеличением [math] m [/math] доля операций первого вычислительного ядра будет расти, а доля операций второго - падать, и наоборот.
1.4 Макроструктура алгоритма
Алгоритм Штрассена состоит из [math] m+1 [/math] рекурсивных шагов и может быть представлен в виде двух этапов.
Первый этап соответствует первым [math] m [/math] рекурсивным шагам, на каждом из которых можно выделить следующие три последовательные макрооперации:
- вычисление матриц [math] S_{i}, T_{i}, \: i = \overline{1, 7} [/math];
- рекурсивный вызов для вычисления произведений [math] \alpha_{i} = S_{i} \cdot T_{i}, \: i = \overline{1, 7} [/math], таким образом при переходе на следующий рекурсивный шаг задача размера [math] k [/math] сводится к семи задачам размера [math] \frac{k}{2} [/math];
- вычисление матрицы [math] C [/math] из матриц [math] \alpha_{i} [/math].
Второй этап соответствует последнему, [math] m+1 [/math]-ому шагу алгоритма и выходу из рекурсии. Он представляет из себя вычисление произведения двух матриц матриц порядка [math] n_{m} = \frac{n}{2^{m}} [/math] по классическому алгоритму:
- [math] c_{ij} = \sum_{k = 1}^{n_{m}} a_{ik} b_{kj}, \: i,j = \overline{1, n_{m}} [/math].
1.5 Схема реализации последовательного алгоритма
Псевдокод простейшего варианта реализации последовательного алгоритма Штрассена, непосредственно вытекающего из его математического описания, может быть записан следующим образом:
Strassen(A, B, C, k, m) ! C = A * B
if (m == 0) call mul(A, B, C, k) ! переход к классическому алгоритму умножения матриц
do i = 1, 7
compute S[i], T[i] from A and B
end do
do i = 1, 7
call Strassen(S[i], T[i], alpha[i], k/2, m-1)
end do
do i = 1, 7
compute parts of C from alpha[i]
end do
end Strassen
Таким образом, на каждом рекурсивном шаге эта схема состоит из трёх последовательных этапов:
- Вычисление семи пар матриц [math] S_{i}, T_{i} [/math]. Так как они определены независимо друг от друга и хранятся в разных областях памяти, порядок их вычисления может быть произвольным, в том числе параллельным.
- Выполнение семи рекурсивных вызовов функции Strassen, по одному для каждой тройки [math] \alpha_{i} = S_{i} \cdot T_{i}[/math]. Порядок этих вызовов также может быть произвольным и параллельным.
- Вычисление матрицы [math] С [/math] из полученных после рекурсивных вызовов матриц [math] \alpha_{i} [/math].
Как видно, данная реализация требует большого количества дополнительной памяти, так как на каждом рекурсивном шаге необходимо одновременно хранить семь пар [math]\frac{k}{2}\times\frac{k}{2}[/math]-матриц [math] S_{i}, T_{i} [/math] и семь результатов их умножения [math] \alpha_{i} [/math].
Есть и другой вариант реализации последовательного алгоритма, позволяющий значительно сократить количество требуемой памяти:
Strassen(A, B, C, k, m) ! C = A * B
if (m == 0) call mul(A, B, C, k) ! переход к классическому алгоритму умножения матриц
do i = 1, 7
compute S[i], T[i] from A and B
call Strassen(S[i], T[i], alpha[i], k/2, m-1)
compute part of C from alpha[i]
end do
end Strassen
На каждом рекурсивном шаге схема этой реализации представляет собой цикл по [math]i = 1,\dotsc,7[/math], каждая итерация которого состоит из трёх последовательных этапов:
- Вычисление [math]i[/math]-ой пары матриц [math] S_{i}, T_{i} [/math].
- Выполнение рекурсивного вызова функции Strassen для вычисления [math] \alpha_{i} = S_{i} \cdot T_{i} [/math].
- Обновление блоков матрицы [math] С [/math] в соответствии с формулами алгоритма в зависимости от номера полученной после рекурсивного вызова матрицы [math] \alpha_{i} [/math].
Порядок итераций такого цикла может быть произвольным, но они должны выполняться строго последовательно. Такое требование позволяет выделить память всего для трёх [math]\frac{k}{2}\times\frac{k}{2}[/math]-матриц на каждом рекурсивном шаге: для одной пары [math] S_{i}, T_{i} [/math] и их произведения [math] \alpha_{i} [/math], и на каждой итерации цикла использовать одни и те же области памяти для хранения соответствующей тройки матриц.
1.6 Последовательная сложность алгоритма
Оба вышеописанных варианта реализации метода Штрассена требуют одинакового числа арифметических операций. В соответствии с макроструктурой алгоритма, рассмотрим каждый из его двух этапов отдельно.
Первый этап требует на первом рекурсивном шаге выполнения [math]18 \left( \frac{n}{2} \right)^2 [/math] сложений (вычитаний). При переходе на следующий рекурсивный шаг, задача будет сведена к семи аналогичным задачам, но вдвое меньшей размерности. Отсюда получаем, что на [math]k[/math]-ом шаге потребуется [math]18 \cdot 7^{k-1} \left( \frac{n}{2^{k}} \right)^2 [/math] операций. Тогда всего на первых [math] m [/math] шагах потребуется следующее число сложений (вычитаний):
- [math] 18 \left( \frac{n}{2} \right)^2 + 18 \cdot 7 \left( \frac{n}{4} \right)^2 + \dotsb + 18 \cdot 7^{m-1} \left( \frac{n}{2^{m}} \right)^2 = \frac{18}{4}n^{2}\left( 1 + \frac{7}{4} + \dotsb + \frac{7^{m-1}}{4^{m-1}}\right) = 6n^2\left(\frac{7^{m}}{4^{m}} - 1 \right) [/math].
Получена сложность первого этапа алгоритма.
Второй этап включает в себя решение [math]7^m[/math] задач перемножения матриц порядка [math] \frac{n}{2^{m}} [/math] по классическому алгоритму, что требует [math]7^m \left(\frac{n}{2^{m}}\right)^3[/math] умножений и [math]7^m \left(\frac{n}{2^{m}}\right)^2\left(\frac{n}{2^{m}}-1\right)[/math] сложений, всего [math]O\left(\frac{n^3}{2^{3m}}\right)[/math] арифметических операций.
Всего последовательный алгоритм Штрассена требует:
- [math]6n^2\left(\frac{7^{m}}{4^{m}} - 1 \right) + 7^m\left(\frac{n}{2^{m}}\right)^2\left(\frac{n}{2^{m}}-1\right)[/math] сложений;
- [math]7^m\left(\frac{n}{2^{m}}\right)^3[/math] умножений.
Как видно, сложность алгоритма зависит не только от порядка матрицы [math] n [/math], но и от числа [math] m [/math] рекурсивных шагов первого этапа.
Если [math] m = L[/math], где [math]n = 2^L[/math], то есть второй этап алгоритма сводится лишь к [math]7^L[/math] умножениям двух чисел, то сложность всего последовательного алгоритма равна
- [math] 6n^2\left(\frac{7^{L}}{4^{L}} - 1 \right) + 7^L\left(\frac{n}{2^{L}}\right)^3 = 6n^2\left(\frac{7^{L}}{n^{2}} - 1 \right) + 7^L = 7 \cdot 7^{L} - 6n^2 = 7 n^{\log_2 7} - 6n^2 = O\left(n^{\log_2 7}\right) \approx O\left(n^{2.81}\right) [/math].
Таким образом, получена оценка сложности последовательного алгоритма Штрассена с максимально возможным числом [math]m = L[/math] рекурсивных шагов, соответствующая максимальной оценке сложности первого этапа алгоритма для произвольного [math]m[/math]. Эта оценка асимптотически лучше оценки для классического метода перемножения матриц, требующего [math]O(n^3)[/math] операций.
Стоит отметить роль правильного выбора параметра [math] m [/math]. Из полученных оценок видно, что при малых [math] m [/math] сложность алгоритма с уменьшением этого параметра будет стремиться к кубической сложности классического метода, а значит [math] m [/math] стоит выбирать относительно близким к [math] L [/math]. Однако, при [math] m [/math], очень близких к [math] L [/math], алгоритм на последних рекурсивных шагах будет применяться на матрицах малых размеров и требовать большего числа сложений, чем классический метод, и эта разница будет увеличиваться с уменьшением размера матрицы, что соответствует увеличению [math] m [/math]. Отсюда следует, что существует некоторое оптимальное значение [math] m \in [1, L] [/math], которое минимизирует число арифметических операций всего алгоритма и выбирается исходя из минимального размера матрицы, на которой описанный в первом этапе рекурсивный алгоритм будет эффективнее классического. Также при выборе [math] m [/math] стоит учитывать роль накладных расходов на реализацию рекурсии при малых размерах матриц.
1.7 Информационный граф
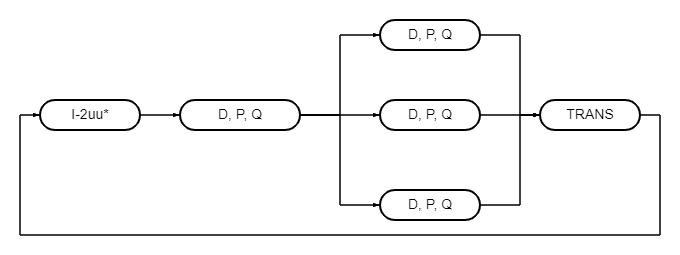
Граф алгоритма зависит от параметра [math] m [/math], то есть от заданного числа рекурсивных шагов. На рисунке изображен граф при [math] m = 1 [/math], отражающий макроструктуру алгоритма (первая схема реализации последовательного алгоритма).
Как видно, на каждом уровне все операции могут выполняться параллельно и независимо друг от друга. При увеличении [math] m [/math] на единицу, число уровней будет увеличиваться на два. Например, на данном графе это означает, что после вычисления всех [math] S_{i}, T_{i} [/math] из входных данных [math] A, B[/math] будут производиться аналогичные вычисления для каждой пары [math] S_{i}, T_{i} [/math]. Таким образом, новый уровень графа будет содержать [math]2 \cdot 49[/math] макроопераций. Из аналогичных соображений после вызовов mul() из возвращаемых значений надо будет сначала вычислить [math] \alpha_{i} [/math] (семь независимых макроопераций), а уже из этих значений получить матрицу [math] С [/math].
1.8 Ресурс параллелизма алгоритма
Для реализации параллельного варианта алгоритма Штрассена небходимо последовательно выполнить следующие ярусы:
- [math] m [/math] ярусов вычисления матриц [math] S_{i}, T_{i} [/math] порядка [math]\frac{n}{2^k}[/math], где [math]k[/math] - номер яруса. Сложность этого этапа равна [math] \frac{n^2}{3}\left(1-\frac{1}{4^m}\right) [/math] операциям сложения.
- Ярус алгоритма классического умножения для матриц порядка [math] \frac{n}{2^{m}} [/math], что требует [math]\left(\frac{n}{2^{m}}\right)^3[/math] умножений и [math]\left(\frac{n}{2^{m}}\right)^2\left(\frac{n}{2^{m}}-1\right)[/math] сложений.
- [math] m [/math] последовательных ярусов вычисления матрицы произведения [math]C[/math] из полученных на предыдущем шаге матриц [math]\alpha_{i}[/math]. Сам процесс вычисления этой матрицы можно разбить на четыре параллельных и независимых вычисления её блоков (исходя из формул математического описания алгоритма), поэтому сложность всего этапа составит [math] n^2 \left(1-\frac{1}{4^m}\right) [/math].
Таким образом, сложность всего параллельного алгоритма составит [math]\frac{4 n^2}{3}\left(1-\frac{1}{4^m}\right) + \left(\frac{n}{2^{m}}\right)^3 + \left(\frac{n}{2^{m}}\right)^2\left(\frac{n}{2^{m}}-1\right) [/math] арифметических операций. При [math]m[/math], близких к [math]L[/math], эта оценка равна [math]O(n^2)[/math], то есть параллельная версия алгоритма Штрассена имеет квадратичную сложность.
Основной ресурс конечного параллелизма алгоритма - независимое вычисление матриц [math] S_{i}, T_{i} [/math] на каждом рекурсивном шаге, причем с каждым шагом их количество возрастает в семь раз. Аналогично, при выходе из рекурсии, вычисление матриц-произведений из [math]\alpha_{i}[/math] производится независимо, причем вычисление каждой из них представимо в виде независимого обновления её четырех блоков.
Более того, можно распараллелить вычисление каждой из матриц [math] S_{i}, T_{i} [/math], так как оно сводится к операции сложения матриц, а значит к независимым операциям сложения элементов или блоков матрицы.
1.9 Входные и выходные данные алгоритма
Входные данные: матрицы [math]A[/math] и [math]B[/math] порядка [math] n [/math], где, в общем случае, [math] n = s \cdot 2^L[/math]. В данной реализации алгоритма в силу блочно-параллельного выполнения операции сложения двух матриц и особенностей их хранения, дополнительно требуется [math] n = s \cdot 7^{\left[\frac{\log_7p+1}{2}\right]} \cdot 2^m[/math], где [math]p[/math] - число процессов.
Объём входных данных: [math]n^2 + n^2[/math].
Выходные данные: матрица [math]C[/math].
Объём выходных данных: [math]n^2[/math].
1.10 Свойства алгоритма
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
3 Литература
- ↑ Тыртышников Е.Е. Матричный анализ и линейная алгебра. М.: 2004-2005.