EM Алгоритм для пуассон трехточечного распределения

Автор: Виктория Евстефеева

1 Свойства и структура алгоритмов

1.1 Общее описание алгоритма

EM-алгоритм (англ. expectation-maximization) - алгоритм итерационного типа для численного решения задачи поиска экстремума целевой функции в разнообразных задачах оптимизации. В частности, алгоритм используется в математической статистике для нахождения оценок максимального правдоподобия параметров вероятностных моделей, в случае, когда модель зависит от некоторых скрытых переменных. Каждая итерация алгоритма состоит из двух шагов. На E-шаге (expectation) вычисляется ожидаемое значение функции правдоподобия, при этом скрытые переменные рассматриваются как наблюдаемые. На M-шаге (maximization) вычисляется оценка максимального правдоподобия, таким образом увеличивается ожидаемое правдоподобие, вычисляемое на E-шаге. Затем это значение используется для E-шага на следующей итерации. Алгоритм выполняется до сходимости.

Как правило, ЕМ-алгоритм применяется для решения задач двух типов.

• К первому типу можно отнести задачи, связанные с анализом действительно неполных данных, когда некоторые статистические данные отсутствуют в силу каких-либо причин.

• Ко второму типу задач можно отнести статистические задачи, в которых функция правдоподобия имеет вид, не допускающий удобных аналитических методов исследования, но допускающий серьезные упрощения, если в задачу ввести дополнительные «ненаблюдаемые» (скрытые, латентные) переменные. Примерами прикладных задач второго типа являются задачи распознавания образов, реконструкции изображений. Математическую суть данных задач составляют задачи кластерного анализа, классификации и разделения смесей вероятностных распределений.

1.2 Математическое описание алгоритма

Задача отыскания наиболее правдопободных оценок параметров смесей вероятностных распределений является одним из самых популярных приложений ЕМ-алгоритма.

Базовым предположением в рамках данной задачи является то, что плотность наблюдаемой случайной величины [math]Χ[/math] имеет вид:

[math]f_{θ}^{X}=Σ_{i=1}^{k}p_{i}ψ_{i}(x; t_{i}),[/math]

где [math]k\geqslant 1[/math] - известное натуральное число, [math]ψ_{1}, ..., ψ_{k}[/math] - известные плотности распределения, неизвестный параметр [math]θ[/math] имеет вид [math]θ=(p_{1}, ..., p_{k}, t_{1},..., t_{k}),[/math] причем [math]p_{i}\geqslant 0,[/math] [math]i = 1, ..., k,[/math] [math] p_{1}+...+p_{k}=1,[/math] [math]t_{i},[/math] [math] i=1,...,k,[/math] - вообще говоря, многомерные параметры. Плотности [math]ψ_{1}, ..., ψ_{k}[/math] будем называть компонентами смеси, параметры [math]p_{1}, ..., p_{k}[/math] будем называть весами соответствующих компонент.

Задачей разделения смеси принято называть задачу статистического оценивания параметров [math]θ=(p_{1}, ..., p_{k}, t_{1},..., t_{k}),[/math] по известным реализациям случайно величины [math]Χ[/math]. Оценивание параметров смешанных пуассоновских моделей сводится к оцениванию смешивающего распределения. Традиционно с этой целью используется классический ЕМ алгоритм. В случае Пуассон трехточечного распределения случайной величины [math]Χ[/math] функция плотности относительно считающей меры имеет вид:

[math]f_{λ, p}^{X}=Σ_{i=1}^{k}p_{i}\frac{λ_{i}^{x}e^{-λ_{i}}}{x!},[/math]

где [math]λ[/math] - трехточечная случайная величина, то есть принимает значения [math]λ_{1}, λ_{2}, λ_{3}[/math] с вероятностями [math]p_{1}, p_{2}, p_{3}[/math] соответственно.

Итерационный ЕМ-алгоритм для оценивания неизвестных параметров [math]p_1,p_2,p_3,λ1,λ_2,λ_3[/math] определяется следующим образом. Дана выборка [math]X_1, ..., X_n[/math] независимых одинаково распределенных случайных величин таких, что

[math]P(X_i = k)=\frac{1}{k!}Σ_{j=1}^{3}p_{j}λ_{j}^{k}e^{-λ_{j}}, k = 0,1,2,...,[/math]

где [math]p_j \geqslant 0, λ_j \gt 0, j = \{1, 2, 3\}[/math] - неизвестные параметры, [math]p_1+p_2+p_3=1[/math]

Пусть [math]p^{(m)}_1, p^{(m)}_2 , p^{(m)}_3, λ_1^{(m)}, λ_2^{(m)}, λ_3^{(m)}[/math] – оценки этих параметров, полученные на [math]m[/math]-й итерации.

Таким образом ЕМ алгоритм для случая пуассон-трехточечного распределения состоит из следующих шагов:

1 шаг алгоритма - вычисление условного математического ожидания:

[math]g_{ij}^{(m)} = \frac{p_j^{(m)}e^{-λ_j^{(m)}}(λ_j^{(m)})^{X_i}}{Σ_{j=1}^{3}p_je^{-λ_j^{(m)}}(λ_j^{(m)})^{X_i}}, i=1,..., n[/math]

2 шаг алгоритма - оценивание неизвестных параметров:

[math]p_j^{(m+1)}=\frac{1}{n}Σ_{i=1}^{n}g_{ij}^{(m)}, j = \{1, 2, 3\}[/math]

[math]λ_j^{(m+1)}=\frac{Σ_{i=1}^{n}X_ig_{ij}^{(m)}}{Σ_{i=1}^{n}g_{ij}^{(m)}}, j = \{1, 2, 3\}[/math]

Функция правдоподобия для пуассон-трехточечного распределения имеет вид:

[math]L(X, λ, p)=Σ_{i=1}^{n}log(Σ_{j=1}^{3}p_{j}λ_{j}^{X_i}e^{-λ_{j}})[/math]

1.3 Вычислительное ядро алгоритма

Основные вычисления связаны с поиском параметров пуассон-трехточечного распределения.

1.4 Макроструктура алгоритма

К исходным данным из пуассон-трехточечного распределения применяется ЕМ алгоритм для разделения смеси.

Проводится несколько итераций запуска ЕМ алгоритма на данных.

После каждой итерации получаем параметры распределения. Считаем функцию правдоподобия.

Если ее значение больше, чем в другой итерации, то эти параметры смеси запоминаются.

1.5 Схема реализации последовательного алгоритма

Здесь приведены основные моменты алгоритма.

// Плотность пуассоновского распределения
double poisson_pdf(int x, double lambda_)
{
    return pow(lambda_,x) * exp(-lambda_) / factorial(x);
}

// Функция правдоподобия для пуассон-трехточечного распределения
double likelihood(vector<int> &X, double *lambda_, double *p)
{
    double summation = 0.0;
    for (int n = 0, length_ext = X.size(); n <  length_ext; ++n)
    {
        double temp = 0.0;
        for (int k = 0; k < 3; ++k)
            temp += p[k] * poisson_pdf(X[n], lambda_[k]);
        summation += log(temp);
    }

    return summation;
}

//Вычисление начального приближения для EM алгоритма
double p[3], lambda_[3];
double minim = -100000.0;
double sum = 0.0;

for (int i = 0; i < K; ++i)
{

    p[i] = rand() % 13371337 + 1;
    sum += p[i];
}


for (int i = 0; i <  K; ++i)
    p[i] /= sum;

for (int i = 0; i < K; ++i)
{
    sum = 0.0;
    int j, l = 0;
    if (i == 0)
        j = 0;
    else
        j = int(N*p[i-1]);
    for (int q = j;  q < int(N*p[i]); ++q)
        sum += X[q];
        l += 1;
    lambda_[i] = sum/l;
}

double likely = likelihood(X, lambda_, p);
double like = minim;
if (likely > minim)
    like = likely;

// ЕМ алгоритм
while (1)
{
    //E-шаг
    for (int i = 0; i < N; ++i)
    {
        double denominator = 0.0;
        for  (int j = 0; j < K; ++j)
            denominator += p[j] * poisson_pdf(X[i], lambda_[j]);
        for (int k = 0; k < K; ++k)
            gamma[i][k] = p[k] * poisson_pdf(X[i], lambda_[k]) / denominator;
    }



    //M-шаг
    for (int k = 0; k < K; ++k)
    {
        double Nk = 0.0;
        for (int n = 0; n < N; ++n)
            Nk += gamma[n][k];

        //Вычисляем среднее
        lambda_[k] = 0.0;
        for (int n = 0; n < N; ++n)
            lambda_[k] += gamma[n][k] * X[n];
        lambda_[k] /= Nk;

        //Вычисляем коэффициенты смешивания
        p[k] = Nk / N;
    }

    double new_like = likelihood(X, lambda_, p);
    double diff = new_like - like;
    if (isnan(diff))
        break;
    if (abs(diff) < 0.0000000001)
        break;
    like = new_like;
}

2 Последовательная сложность алгоритма

Вычислим последовательную сложность алгоритма, основываясь на начальных данных и количестве повторов итераций запуска ЕМ алгоритма.

[math]w[/math] - количество итераций запуска ЕМ алгоритма

[math]h[/math] - количество данных

На каждой итерации ищутся параметры смеси: [math]k\cdot O(h)[/math], где [math]k[/math] - некоторая константа, которая зависит от начального приближения параметров и влияет на скорость сходимости ЕМ алгоритма, для каждой итерации может быть разной.

В итоге получаем [math]O(k \cdot w \cdot h)[/math] операций.

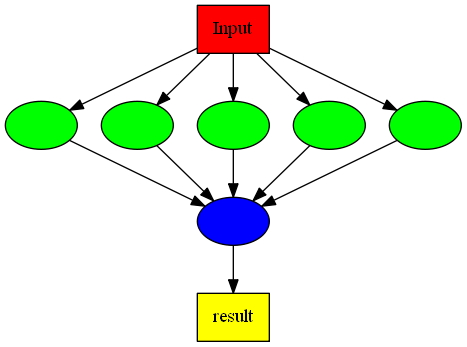
3 Информационный граф

Зеленые вершины - вычисление параметров ЕМ алгоритма.
Желтые вершины - вычисление функции правдоподобия.

3.1 Ресурс параллелизма алгоритма

Из информационного графа видно, что вычисление параметров ЕМ алгоритма и функции правдоподобия на разных итерациях происходит независимо от других, затем они завершаются и первый процесс записывает результат в файл. Пусть [math]N_p \geqslant 2[/math] - количество процессов. Всем процессам поручим выполнить часть итераций запуска ЕМ алгоритма (каждый процесс выполнит [math]\Big[\frac{w}{N_p - 1}\Big] [/math] итераций). Первому процессу поручим принять работу и записать результат в файл.

Время работы: [math]O\Big(\frac{k \cdot w \cdot h}{N_p}\Big)[/math].

3.2 Входные и выходные данные алгоритма

На вход алгоритму подаются данные из пуассон-трехточечного распределения.

На выходе получаем параметры смеси.

4 Программная реализация алгоритма

4.4 Масштабируемость алгоритма и его реализации

Исследование проводилось на суперкомпьютере "Ломоносов".

Компилятор C++
impi 5.1.0

a) Количество данных - 100000, количество итераций 256.

Число процессов	Время (с)
1	40.402
2	20.654
4	10.998
8	3.541
16	3.568
32	3.153
64	3.690
128	6.233

Алгоритм перестает масштабироваться, когда время работы параллельной части алгоритма (вычисление параметров) мало по сравнению с накладными расходами MPI и временем, которое расходуется на загрузку данных.

б) Количество данных - 100000, количество итераций 8192.

Число процессов	Время (с)
1	Ломоносов не досчитал, время вышло
2	647.435
4	323.948
8	162.607
16	83.009
32	42.897
64	23.928
128	16.545

Алгоритм сильно масштабируется. Время выполнения алгоритма сокращается почти в 2 раза с увеличением количества ресурсов в 2 раза.

5 Литература

↑ В.Ю. Королев "Вероятностно-статистические методы декомпозиции волатильности хаотических процессов".

↑ В. Ю. Королев, А. Ю. Корчагин, А. И. Зейфман "Теорема Пуассона для схемы испытаний Бернулли со случайной вероятностью успеха и дискретный аналог распределения Вейбулла".

↑ http://www.machinelearning.ru/wiki/index.php?title=EM-алгоритм