BiCGStab, HYPRE
Основные авторы описания: А.Новиков (раздел 3).
Содержание
1 Ссылки
Параллельная реализация алгоритма в бесплатной библиотеке, поддерживающей MPI и OpenMP, HYPRE: Официальная страница Исходный код.
2 Локальность данных и вычислений
2.1 Локальность реализации алгоритма
2.1.1 Структура обращений в память и качественная оценка локальности
2.1.2 Количественная оценка локальности
3 Масштабируемость алгоритма и его реализации
3.1 Масштабируемость алгоритма
3.2 Масштабируемость реализации алгоритма
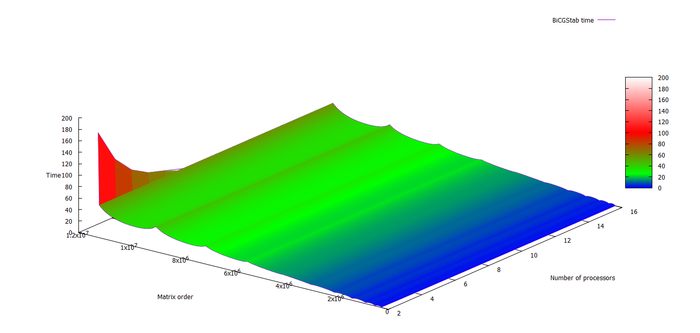
Исследование масштабируемости реализации стабилизированного метода бисопряженных градиентов проводилось согласно методике на суперкомпьютере "Ломоносов"[1] Суперкомпьютерного комплекса Московского университета.
Набор и границы значений изменяемых параметров запуска реализации алгоритма:
- число процессоров [2 : 16] с шагом 1;
- размер матрицы [262144 : 11239424].
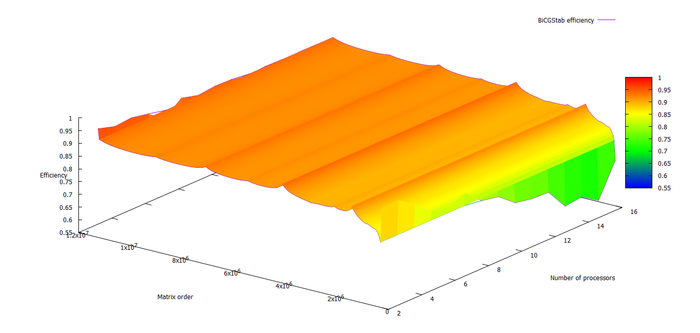
В результате проведённых экспериментов был получен следующий диапазон эффективности реализации алгоритма:
- минимальная эффективность реализации 60,00%;
- максимальная эффективность реализации 98,33%.
На следующих рисунках приведены графики производительности и эффективности выбранной реализации стабилизированного метода бисопряженных градиентов в зависимости от изменяемых параметров запуска.
4 Динамические характеристики и эффективность реализации алгоритма
5 Результаты прогонов
6 Литература
- ↑ Воеводин Вл., Жуматий С., Соболев С., Антонов А., Брызгалов П., Никитенко Д., Стефанов К., Воеводин Вад. Практика суперкомпьютера «Ломоносов» // Открытые системы, 2012, N 7, С. 36-39.