Участница:Полина Кривуля/Сеть битонной сортировки

1 Свойства и структура алгоритмов

1.1 Общее описание алгоритма

Битонная сортировка – это параллельный алгоритм сортировки, основанный на использовании понятия битонной последовательности. Алгоритм разработан американским информатиком Кеннетом Бэтчером в 1968 году и является одним из старейших параллельных алгоритмов сортировки. Наряду с четно-нечетной сортировкой слиянием, является одним из первых методов построения сортировочной сети для любого количества входов . Публикация этого алгоритма, наряду с также предложенным Бэтчером алгоритмом сеть нечетно-четной перестановки, стимулировала развитие проектирования и анализа параллельных алгоритмов в общем и параллельной сортировки в частности.

Битонной последовательностью называют последовательность, которая монотонно не убывает, а затем монотонно не возрастает, либо приводится к такому виду в результате циклического сдвига. Пример такой последовательности – {8, 10, 16, 12, 4, -2, -8} . Любая последовательность, входящая в битонную, любая последовательность состоящая из одного или двух элементов, а также любая монотонная последовательность также является битонной. Например, последовательности {3,5,10,4,1}, {1,5}, {10,14,5,-1,-4} являются битонными, а {4,6,1,9,2} не является. Каждое множество неотсортированных элементов можно считать множеством битонных последовательностей, состоящих из двух элементов. Процесс битонного слияния преобразует битонную последовательность в полностью отсортированную последовательность. Алгоритм битонной сортировки состоит из применения битонных преобразований до тех пор, пока множество не будет полностью отсортировано .

Время работы алгоритма составляет [math] O(log^2(n))[/math] (в случае использования параллелизма).

1.2 Математическое описание алгоритма

Сортировкой, или упорядочиванием элементов, называется процесс их расположения согласно определенному линейному отношению порядка, такому как отношение «меньше или равно» для чисел. На вход поступает неотсортированный массив чисел. Выходными данными алгоритма является массив, отсортированный в порядке неубывания или невозрастания.

Решение задачи основано на понятии битонной последовательности. Исходный массив преобразуется в битонную последовательность. Для этого нужно разделить последовательность пополам, первую часть рекурсивно отсортировать по возрастанию, вторую часть рекурсивно отсортировать по убыванию .

Разделим преобразованный массив на две части: первый массив отсортирован в порядке неубывания, второй в порядке невозрастания. Последовательно сравниваем элементы из двух массивов. Если какой-либо элемент из второго массива окажется меньше соответствующего элемента из первого массива, меняем его местами с элементом из первого массива. В результате в первом массиве окажутся наименьшие элементы из обоих массивов, а во втором - наибольшие. При этом каждый из массивов будет являться битонной последовательностью, каждую из которых можно рекурсивно отсортировать тем же образом, после чего можно склеить два массива (так как любой элемент первого меньше или равен любого элемента второго).

В данном алгоритме необходимо, чтобы размер исходного массива был равен степени двойки. В противном случае, его придется дополнять фиктивными элементами, что, однако, не влияет не асимптотику .

1.3 Вычислительное ядро алгоритма

Вычислительное ядро алгоритма битонной сортировки можно представить следующим образом :

1. Разбиение исходного массива на битонные последовательности.

2. Сортировка каждой битонной последовательности в порядке возрастания.

3. Объединение отсортированных битонных последовательностей.

1.4 Макроструктура алгоритма

В начале программы генерируется массив случайных чисел, но время генерации массива не засекается.

Для преобразования исходных данных в битонные последовательности используется библиотечная функция быстрой сортировки. Также используются минимальные и максимальные члены массивов каждого процесса для обмена данными между парными процессами.

Парные процессы обмениваются элементами своих массивов так, чтобы при дальнейшем слиянии массивов образовался уже отсортированный массив и не было необходимости использовать слияние для получения конечного массива.

1.5 Схема реализации последовательного алгоритма

Исходный массив преобразуется в битонную последовательность. Для того, чтобы преобразовать исходный массив в битонную последовательность разделяем массив пополам, рекурсивно вызоваем от половинок алгоритм сортировка, после чего сортируем первую часть по порядку, вторую в обратном порядке и склеиваем. Получается битонная последовательность. Ее можно эффективно отсортировать следующим образом: разобьем массив на две части, создадим два массива, в первый добавим все элементы, равные минимуму из соответственных элементов каждой из двух частей, а во второй – равные максимуму. Получатся две битонные последовательности, каждую из которых можно рекурсивно отсортировать тем же образом, после чего можно склеить два массива. Получится отсортированный массив.

Сложность такой реализации [math] O(nlog^2n)[/math] поскольку при построении битонной последовательности мы использовали сортировку, работающую за [math] O(nlogn)[/math], а всего уровней было [math] logn[/math].

1.6 Последовательная сложность алгоритма

Сложность алгоритма битонной сортировки зависит от количества элементов в массиве. Обозначим эту величину как [math]n[/math].

В каждом шаге рекурсивной сортировки, массив разбивается на две части, и каждая из этих частей сортируется отдельно. Таким образом, каждый шаг рекурсии занимает [math]O(nlog(n))[/math] времени. Всего шагов рекурсии [math]log(n)[/math], так как на каждом шаге размер массива уменьшается вдвое.

Таким образом, общая сложность последовательного алгоритма битонной сортировки составляет [math]O(n log^2(n))[/math].

1.7 Информационный граф

Информационный граф битонной сортировки

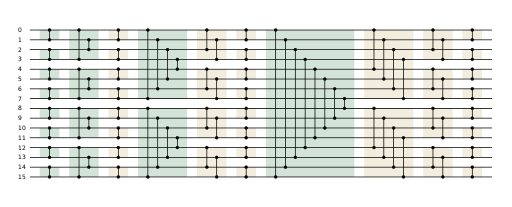
Диаграмма сортировки для 16 сортируемых элементов. Горизонтальные линии представляют индексы массива в нашем массиве сортируемых элементов, каждая вертикальная линия представляет один рабочий поток, выполняющий операцию сравнения и замены.

На диаграмме каждый рабочий поток нарисован в виде вертикальной линии, начальная и конечная точки обозначают индексы текущей пары сортируемых элементов. Все цветные блоки, находящиеся в одном столбце, образуют шаг, который можно выполнять параллельно. Из диаграммы видно, что количество потоков на шаг постоянно и всегда равно [math] n/2[/math], где [math] n[/math] — количество сортируемых элементов .

1.8 Ресурс параллелизма алгоритма

Алгоритм дает большой выигрыш при использовании параллелизма. В общем случае можно распараллелить данный алгоритм на любое число процессов кратное двум. Однако следует учитывать накладные расходы на создание MPI процессов и обмен сообщениями между ними. Если их будет достаточно много для сравнительно небольшой длины массива, то выигрыш в производительности будет очень маленьким, либо может отсутствовать вовсе.

При последовательной реализации каждый шаг рекурсии занимает [math]O(nlog(n))[/math] времени, а всего шагов рекурсии [math]log(n)[/math].

В параллельной реализации временная сложность алгоритма гораздо меньше - [math]O(log^2n)[/math].

1.9 Входные и выходные данные алгоритма

Исходные данные: одномерный массив [math]A[/math], содержащий [math]n[/math] элементов, [math]|A|=n[/math].

Выходные данные: упорядоченный массив [math]B=sort(A)[/math].

1.10 Свойства алгоритма

Временная сложность алгоритма:

• При последовательной реализации [math]O(nlog^2(n))[/math]
• При параллельной реализации [math]O(log^2(n))[/math]

Использование памяти:

• Для последовательной реализации в худшем случае [math]O(nlog^2(n))[/math]
• В случае использования параллелизма количество памяти зависит от реализации

Преимущества:

• Не очень сложно реализуется для случая использования параллелизма
• Более эффективен, чем алгоритм быстрой сортировки

Недостатки:

•  Количество сравнений в алгоритме бетонной сортировки обычно больше, чем в других более популярных алгоритмах сортировки