Схема Горнера, вещественная версия, последовательный вариант

Схема Горнера для деления многочлена n-й степени на приведённый двучлен
Последовательный алгоритм
Последовательная сложность	[math]2n[/math]
Объём входных данных	[math]n+2[/math]
Объём выходных данных	[math]n+1[/math]
Параллельный алгоритм
Высота ярусно-параллельной формы	[math]2n[/math]
Ширина ярусно-параллельной формы	[math]1[/math]

Основные авторы описания: А.В.Фролов, Вад.В.Воеводин (раздел 2.2), А.М.Теплов (раздел 2.4)

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

1.1.1 Решаемая задача

Схема Горнера решает задачу деления многочлена [math]P_n(x)[/math] с известными коэффициентами на двучлен [math]x - \alpha[/math]. В качестве результатов выступают коэффициенты многочлена [math]Q_{n - 1}(x)[/math] из соотношения

[math]P_n(x) - P_n(\alpha) = (x - \alpha) Q_{n - 1}(x)[/math],

а также [math]P_n(\alpha)[/math] (значение многочлена [math]P_n(x)[/math] в точке [math]\alpha[/math])

К сожалению, зачастую в учебной литературе схему Горнера сводят к вычислению значения многочлена [math]P_n(x)[/math] в точке [math]\alpha[/math].

1.1.2 Общая схема

Фактически схема Горнера реализует «деление уголком» многочлена на двучлен [math]x - \alpha[/math], с нахождением остатка, который, по теореме Безу, равен значению многочлена [math]P_n(x)[/math] в точке [math]\alpha[/math].

1.2 Математическое описание алгоритма

Исходные данные: одномерный массив [math]n + 1[/math] чисел [math]a_k[/math] и скаляр [math]\alpha[/math].

Вычисляемые данные: одномерный массив [math]n + 1[/math] чисел [math]b_k[/math].

Формулы метода с выводом: из соотношения

[math]P_n(x) - P_n(\alpha) = (x - \alpha) Q_{n - 1}(x)[/math]

если записать оба многочлена в каноническом виде

[math] \begin{align} P_n(x) & = a_0 x^n+ a_1 x^{n - 1} + \dots + a_{n - 1} x + a_n, \\ Q_{n - 1}(x) & = b_0 x^{n - 1} + b_1 x^{n - 2} + \dots + b_{n - 2} x + b_{n - 1} \end{align} [/math]

и приписать «свободному» [math]b_n[/math] значение [math]P_n(\alpha)[/math], то, при подстановке многочленов в каноническом виде в исходное соотношение и приравнивании коэффициентов равных степеней, в качестве решения получается

[math] \begin{align} b_0 & = a_0, \\ b_k & = a_k + \alpha b_{k - 1}, \quad k = 1, \dots, n \end{align} [/math]

что и является формулами схемы Горнера.

1.3 Вычислительное ядро алгоритма

Вычислительное ядро схемы Горнера в последовательном варианте можно представить в качестве последовательного набора [math]n[/math] «двойных» операций (умножение элементов получаемого массива на один и тот же скаляр и добавление результата к следующему элементу входного массива).

1.4 Макроструктура алгоритма

Как уже записано в описании ядра алгоритма, основную часть вычисления схемы Горнера произведения составляет массовый последовательный набор «двойных› операций (умножение элементов получаемого массива на один и тот же скаляр и добавление результата к следующему элементу входного массива).

1.5 Схема реализации последовательного алгоритма

Формулы метода описаны выше. Последовательность исполнения — по возрастанию индекса k.

1.6 Последовательная сложность алгоритма

Для вычисления схемы Горнера для многочлена степени [math]n[/math], количество операций умножения равно количеству операций сложения и равно [math]n[/math]. Поэтому алгоритм должен быть отнесён к алгоритмам линейной сложности по количеству последовательных операций.

1.7 Информационный граф

На рис.1 изображён граф алгоритма для [math]n = 9[/math]. Как видно, граф чисто последовательный. Ввод и вывод обозначен только для начального коэффициента и значения многочлена. Op - операция "умножить входное данное на скаляр и прибавить к другому данному".

Рисунок 1. Схема Горнера: последовательная версия

1.8 Ресурс параллелизма алгоритма

Последовательный вариант вычисления схемы Горнера не имеет ресурсов параллелизма. Его ярусно-параллельная форма (ЯПФ) — единственна и совпадает с последовательным алгоритмом. Таким образом, в получившемся алгоритме высота параллельной формы будет равна [math]n[/math] операций умножения плюс [math]n[/math] операций сложения. В таком виде алгоритм должен быть отнесён к алгоритмам линейной сложности по высоте параллельной формы. Ширина параллельной формы равна [math]1[/math], что даёт нам постоянную сложность по ширине параллельной формы.

1.9 Входные и выходные данные алгоритма

Входные данные: массив [math]a[/math] (элементы [math]a_i[/math] с номерами от [math]0[/math] до [math]n[/math]), скаляр [math]\alpha[/math].

Дополнительные ограничения: отсутствуют.

Объём входных данных: [math]n + 2[/math].

Выходные данные: массив [math]b[/math] (элементы [math]b_k[/math] с номерами от [math]0[/math] до [math]n[/math]).

Объём выходных данных: [math]n + 1[/math].

1.10 Свойства алгоритма

Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов, как хорошо видно, является константой (1). При этом вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных — всего-навсего 1 (входных и выходных данных даже на 1 больше, чем количество операций). При этом алгоритм полностью детерминирован. Дуги информационного графа локальны. По устойчивости схема Горнера оптимальна для вычисления значения многочлена с известными коэффициентами.

2 Программная реализация алгоритма

2.1 Особенности реализации последовательного алгоритма

На Фортране схему Горнера можно записать так:

	b(0) = a(0)
	DO I = 1, N
		b(I) = a(I)+b(I-1)*alpha
	END DO

2.2 Локальность данных и вычислений

Как видно по графу алгоритма, локальность данных по пространству хорошая - все перевычисляемые аргументы, что нужны операциям, вычисляются "рядом". При этом, однако, схема Горнера относится к таким последовательным алгоритмам, в которых локальность вычислений настолько велика, что будет излишней. Из-за того, что данные, нужные для вычислений основных операций алгоритма, вычисляются в его процессе операциями, непосредственно предшествующими им, возможности вычислительных ядер процессоров по использованию своей суперскалярности практически сводятся на нет, что резко ухудшает эффективность исполнения схемы даже на современных однопроцессорных и одноядерных системах.

2.2.1 Локальность реализации алгоритма

2.2.1.1 Структура обращений в память и качественная оценка локальности

Рисунок 2. Реализация схемы Горнера. Общий профиль обращений в память

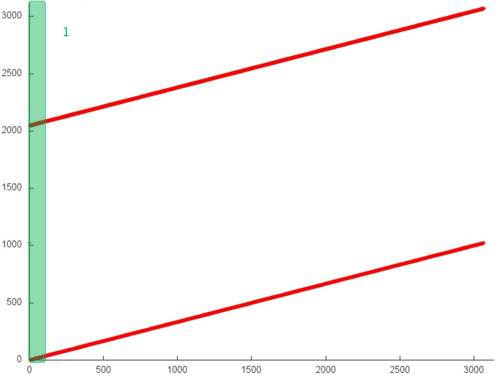
На рис.2 представлен профиль обращений в память последовательной вещественной реализации схемы Горнера. Исходя из рисунка 2, данный профиль устроен очень просто и состоит из двух последовательных переборов элементов, выполняемых параллельно для двух массивов.

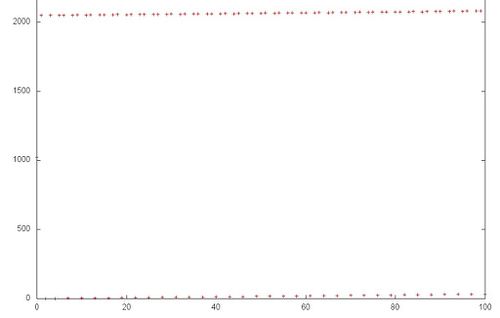
Однако даже в таком простом примере для полного понимания структуры обращений в память нужен более детальный анализ на уровне отдельных обращений. На рис.3 рассмотрим подробнее фрагмент 1, выделенный на рис.2 зеленым. Можно увидеть, что верхний последовательный перебор несколько отличается от нижнего – в первом случае к каждому элементу выполняется по два обращения подряд. Отметим, однако, что данное уточнение строения профиля слабо сказывается на локальности всего профиля.

В целом, общий профиль обладает высокой пространственной локальностью, поскольку перебор элементов массивов осуществляется последовательно, однако очень низкой временно́й локальностью – в одном из массивов к каждому элементу выполняется обращение только дважды, во втором массиве повторные обращения вообще отсутствуют.

Рисунок 3. Фрагмент 1 (первые 100 обращений общего профиля)

2.2.1.2 Количественная оценка локальности

Основной фрагмент реализации, на основе которого были получены количественные оценки, приведен здесь (функция KernelHorner). Условия запуска описаны здесь.

Первая оценка выполняется на основе характеристики daps, которая оценивает число выполненных обращений (чтений и записей) в память в секунду. Данная характеристика является аналогом оценки flops применительно к работе с памятью и является в большей степени оценкой производительности взаимодействия с памятью, чем оценкой локальности. Однако она служит хорошим источником информации, в том числе для сравнения с результатами по следующей характеристике cvg.

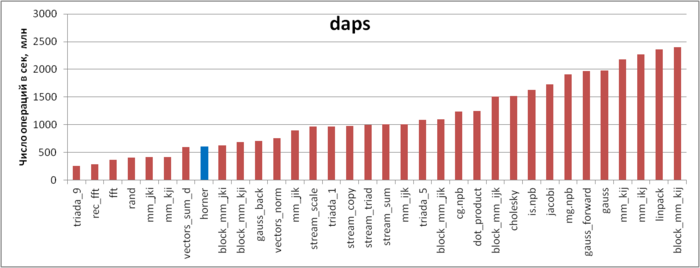
На рис.4 приведены значения daps для реализаций распространенных алгоритмов, отсортированные по возрастанию (чем больше daps, тем в общем случае выше производительность). Согласно данному рисунку, реализация схемы Горнера показывает низкую производительность работы с памятью. Может показаться странным, что значение daps в этом случае значительно меньше, чем для тестов STREAM, несмотря на то, что профиль обращений во всех случаях очень похож – несколько одновременно выполняемых последовательных переборов массивов.

Причина такого поведения связана с особенностями строения подсистемы памяти. В реализации схемы Горнера, как было отмечено выше, к элементам одного из массивов выполняется по два обращения подряд. Однако если посмотреть исходный код реализации, можно увидеть, что на самом деле второе обращение выполняется на следующей итерации – это обращение к предыдущему элементу:

for (int i = 1; i < size; i++) {
    c[i] = a[i] + c[i - 1] * x;
}

В результате из-за зависимости итераций аппаратный префетчер гораздо хуже справляется с подтягиванием требуемых кэш-строк, что приводит к заметному замедлению выполнения программы по сравнению с другими реализациями, основанными на последовательном переборе (например, тесты STREAM).

Подобный пример лишний раз показывает, насколько сложно утроена подсистема памяти – совсем небольшое изменение строения тела цикла приводит к достаточно неожиданному серьезному замедлению программы.

Рисунок 4. Сравнение значений оценки daps

Вторая характеристика – cvg – предназначена для получения более машинно-независимой оценки локальности. Она определяет, насколько часто в программе необходимо подтягивать данные в кэш-память. Соответственно, чем меньше значение cvg, тем реже это нужно делать, тем лучше локальность.

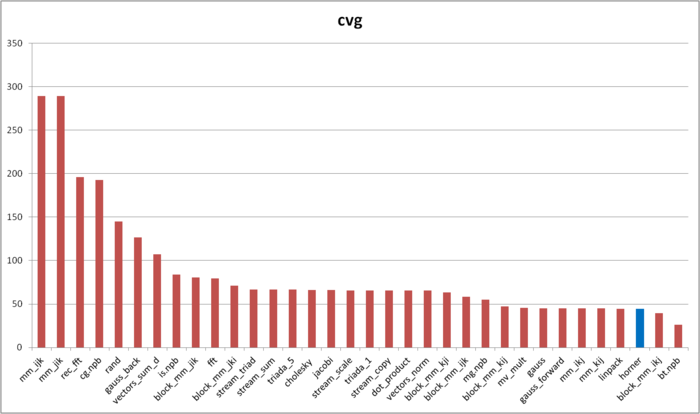
На рис.5 приведены значения cvg для того же набора реализаций, отсортированные по убыванию (чем меньше cvg, тем в общем случае выше локальность). Можно увидеть, что реализация схема Горнера обладает очень высокой локальностью согласно оценке cvg.

Рисунок 5. Сравнение значений оценки cvg

Как мы видели ранее, это плохо соотносится с реальной производительностью работы с памятью из-за особенностей строения памяти. Однако здесь необходимо сделать два замечания. Во-первых, подобные случаи, когда производительность работы с памятью настолько сильно зависит от специфичных аппаратных особенностей строения подсистемы памяти, на практике встречаются не так часто. Во-вторых, cvg предназначена для получения машинно-независимой оценки локальности; на данном уровне учесть подобные аппаратные особенности, по крайней мере, без потери доли машинно-независимых свойств, вряд ли представляется возможным.

2.3 Возможные способы и особенности параллельной реализации алгоритма

Описываемый алгоритм не предполагает параллельной реализации.

2.4 Масштабируемость алгоритма и его реализации

Понятие масштабируемости неприменимо, поскольку описываемый алгоритм не предполагает параллельной реализации. Проведём исследование масштабируемости вширь реализации алгоритма согласно методике. Исследование проводилось на суперкомпьютере "Ломоносов" Суперкомпьютерного комплекса Московского университета. Набор и границы значений изменяемых параметров запуска реализации алгоритма:

• число процессоров 1;
• размер области [10240 : 1024000] с шагом 10240.

В результате проведённых экспериментов был получен следующий диапазон эффективности реализации алгоритма:

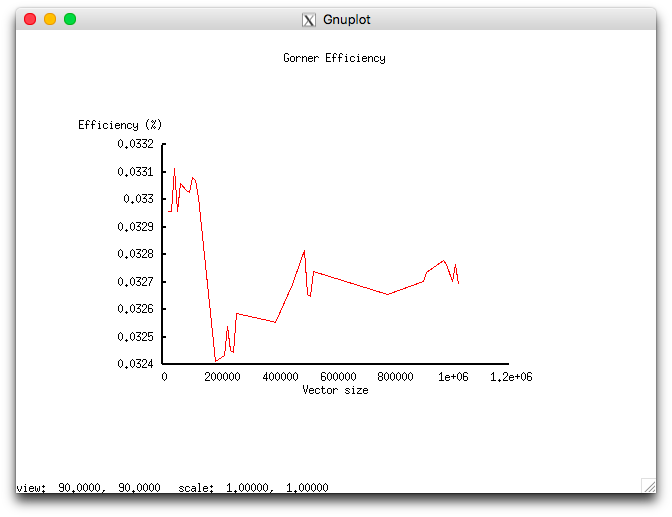
• минимальная эффективность реализации 0.0324%;
• максимальная эффективность реализации 0.0331%.

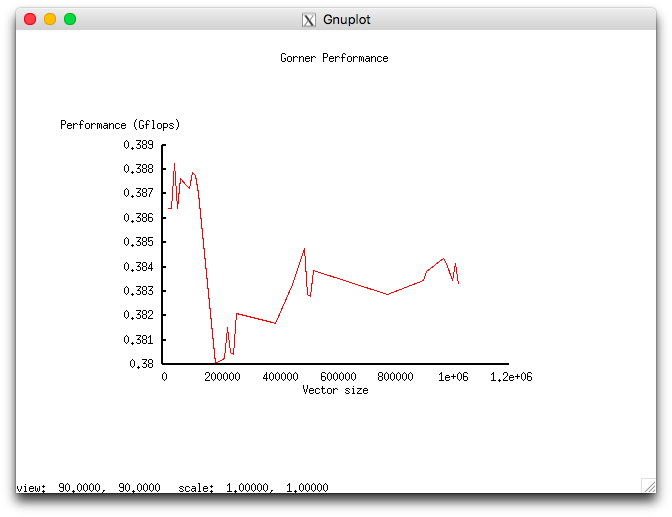
На следующих рисунках приведены графики производительности и эффективности выбранной реализации алгоритма в зависимости от изменяемых параметров запуска.

Рисунок 6. Реализация алгоритма. Изменение производительности в зависимости от размера вектора.

Рисунок 7. Реализация алгоритма. Изменение эффективности в зависимости от размера вектора.

Мизерная эффективность, по-видимому, связана с избыточной локальностью, описанной в разделе о локальности данных и вычислений.

Исследованная здесь (функция KernelHorner). Условия запуска описаны реализация алгоритма

2.5 Динамические характеристики и эффективность реализации алгоритма

В силу последовательности алгоритма и его избыточной локальности, исследование его динамических характеристик малоценно и потому не проводилось.

2.6 Выводы для классов архитектур

Схема Горнера - метод для архитектуры классического, фон-неймановского типа. Даже на современных суперскалярных одноядерных системах эффективность её исполнения очень низка.

2.7 Существующие реализации алгоритма

Помимо выписанной выше простейшей реализации, существуют более примитивные коды, реализующие часть функционала схемы Горнера. Это объясняется тем, что для многих нужно только значение многочлена (остаток от деления), но не нужен многочлен-частное. В таком случае вместо всех элементов массива [math]b[/math] используется один и тот же скаляр.