Участник:Мария Готман/Алгоритм кластеризации, основанный на максимизации ожидания

Материал из Алговики
Перейти к навигации Перейти к поиску

Авторы описания: Готман М.Л., Лукашкина Ю.Н.

1 ЧАСТЬ. Свойства и структура алгоритмов

1.1 Общее описание алгоритма

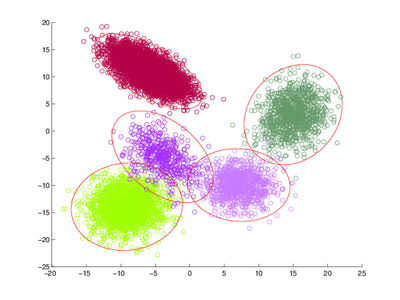
Задача кластеризации — это задача разбиения заданной входной выборки объектов на непересекающиеся подмножества, называемые кластерами, так, чтобы каждый кластер состоял из схожих объектов, а объекты разных кластеров существенно отличались.

Для решения этой задачи можно использовать, например, метод максимизации ожидания, также известный как EM-алгоритм (англ. expectation-maximization). В таком случае делается предположение, что входные данные — смесь многомерных нормальных распределений, соотвественно отдельный кластер — это одна компонента смеси. Предполагается, что количество кластеров является входным параметром алгоритма (существуют модификации EM-алгоритма, которые автоматически находят число кластеров, но они не рассматриваются в данной статье). Результат работы EM-алгоритма — веса кластеров и найденные параметры нормальных распределений для каждого кластера: вектора математических ожиданий и матрицы ковариации.

Алгоритм EM кластеризации основан на итеративном выполнении двух последовательных шагов: E-шага и M-шага. На E-шаге вычисляеются вспомогательные (скрытые) переменные, которые характеризуют апостериорную вероятность того, что определенный обучающий объект получен из фиксированной компоненты смеси. На M-шаге с помощью вычесленных скрытых переменных производится обновление параметров смеси: по определённым формулам пересчитываются веса кластеров, их математические ожидания и матрицы ковариаций.

Стоит отметить, что на работу EM-алгоритма значительно влияет начальное приближение его параметров. При неудачной инициализации алгоритм может не сойтись или сойтись в локальный экстремум.

В данной статье рассматривается частный случай EM-алгоритма, который работает с двумерными входными данными.

Пример работы EM-алгоритма для 4х кластеров.

1.2 Математическое описание алгоритма

Рассматривается смесь нормальных распределений [math]p(x)=\sum_{j=1}^kw_jp_j(x), \sum_{j=1}^kw_j =1, w_j \ge 0[/math].

Алгоритм кластеризации, основанный на максимизации правдоподобия, итеративно выполняет два шага: E-шаг и M-шаг. Идея алгоритма заключается в введении матрицы скрытых переменных [math]G[/math], где [math]g_{ij} \equiv P(\theta_j |x_i)[/math] обозначает вероятность принадлежности [math]i[/math]-го объекта [math]j[/math]-му кластеру.

На Е-шаге вычисляется ожидаемое значение скрытых переменных, на М-шаге выполняется максимизация логарифма полного правдоподобия, результатом которой являются новые значения параметров модели.

На вход алгоритму подается матрица объектов-признаков [math]X \in \R^{m \times d}[/math] и [math]k[/math] — количество кластеров.

На выходе получаем набор параметров модели для каждого кластера [math]\Theta = (w_1,...,w_k;\;\mu_1,...,\mu_k;\;\Sigma_1,...,\Sigma_k)[/math], где [math]w_j[/math] — вес [math]j[/math]-го кластера в смеси нормальных распределений, [math]\mu_j[/math] — математическое ожидание [math]j[/math]-ой компоненты смеси, [math]\Sigma_j[/math] — матрица ковариации [math]j[/math]-ой компоненты смеси.

E-шаг:

[math]g_{ij} = \frac{w_jN(x_i;\mu_j, \Sigma_j)}{\sum_{s=1}^k w_sN(x_i;\mu_s, \Sigma_s)}[/math]

M-шаг:

[math]Q(\Theta) = \ln\prod_{i=1}^mp(x_i) = \sum_{i=1}^m\ln\sum_{j=1}^kw_jp_j(x_i) \rightarrow \max_{\Theta}[/math], при условии [math]\sum_{j=1}^kw_j=1[/math], где

[math]p_j(x_i) = N(x_i;\mu_j, \Sigma_j) = \frac1{(2\pi)^{d/2}\sqrt{|\Sigma_j|}} \exp \biggl(-\frac{1}{2}(x_i - \mu_j) \Sigma_j^{-1} (x_i - \mu_j)^T\biggr) [/math]

Решением оптимизационной задачи являются формулы для пересчета параметров:

[math]w_j = \frac1m\sum_{i=1}^m g_{ij}[/math],

[math]\mu_j = \frac1{mw_j}\sum_{i=1}^m g_{ij}x_i[/math],

[math]\Sigma_j = \frac1{mw_j}\sum_{i=1}^m g_{ij}(x_i - \mu_j)(x_i - \mu_j)^T,\; j = 1, \dots, k[/math]

1.3 Вычислительное ядро алгоритма

Вычислительное ядро алгоритма представляет собой итерационное вычисление всех параметров модели, независимое по [math]m[/math] объектам выборки [math]X[/math]. На каждой итерации алгоритма на Е-шаге пересчитывается значение скрытых переменных, на M-шаге пересчет параметров модели с учетом скрытых переменных.

1.4 Макроструктура алгоритма

Как записано в описании ядра алгоритма, основную часть метода составляют вычисления элементов матрицы G на E шаге, и пересчет параметров [math]\Theta[/math] на M-шаге.

1.5 Схема реализации последовательного алгоритма

  1. Инициализация параметров
  2. for iter = 1 : max_iterations
  3. [E-шаг]
    1. вычисление [math]\Sigma_j^{-1}[/math] и [math]\frac1{(2\pi)^{d/2}\sqrt{|\Sigma_j|}}, j = 1 : k[/math]
    2. вычисление [math]g_{ij},\;i = 1 : m, \; j = 1 : k[/math]
    3. вычисление [math]LL_i[/math] (логарифм правдоподобия), [math]\;i = 1 : m[/math]
  4. [M-шаг]
    1. вычисление [math]\tilde w_j = \sum_{i=1}^m g_{ij}, \; j = 1 : m[/math]
    2. вычисление [math]\tilde \mu_j = \sum_{i=1}^m g_{ij}x_i,\; j = 1 : k[/math]
    3. вычисление [math]\tilde \Sigma_j = \sum_{i=1}^m g_{ij}(x_i - \mu_j)^T(x_i - \mu_j),\; j = 1 : k[/math]
    4. нормировка [math]w_j = \frac{\tilde w_j}{m}[/math], [math]\mu_j = \frac{\tilde \mu_j}{w_j}, \tilde \Sigma_j = \frac{\tilde \Sigma_j}{w_j}, \;j = 1 : k[/math]
  5. вычисление изменения логарифма правдоподобия[math]\Delta LL[/math]
  6. if ([math]\Delta LL \lt \varepsilon[/math]) then break;
  7. end for

1.6 Последовательная сложность алгоритма

E-шаг:

  1. вычисление обратной матрицы [math]\Sigma_j^{-1}, j = 1 : k[/math] при фиксированном [math]j[/math] для двумерного случая по явным формулам имеет сложность [math]O(d^2)[/math], для всех кластеров — [math]O(d^2k)[/math]
  2. вычисление [math]g_{ij}, i = 1 : m, j = 1 : k[/math] при фиксированных [math]i, j[/math] имеет сложность [math]O(d)[/math], сложность вычисления матрицы G — [math]O(dmk)[/math]
  3. вычисление [math]LL_i, i = 1 : m[/math] при фиксированном [math]i[/math] имеет сложность [math]O(k)[/math], для всех объектов имеет сложность [math]O(mk)[/math],

M-шаг:

  1. вычисление [math]w_j, j = 1 : k[/math] при фиксированном [math]j[/math] имеет сложность [math]O(m)[/math], для весов всех кластеров — [math]O(mk)[/math]
  2. вычисление [math]\mu_j, j = 1 : k[/math] при фиксированном [math]j[/math] имеет сложность [math]O(dm)[/math], для всех кластеров — [math]O(dmk)[/math]
  3. вычисление [math]\Sigma_j, j = 1 : k[/math] при фиксированном [math]j[/math] имеет сложность [math]O(d^2m)[/math], для всех кластеров — [math]O(d^2mk)[/math]
  4. нормировка [math]w[/math], [math]\mu_j = \frac{\mu_j}{w_j}, \Sigma_j = \frac{\Sigma_j}{w_j}, j = 1 : k[/math] имеет сложность [math]O(k)[/math], [math]O(dk)[/math], [math]O(d^2k)[/math]
  5. вычисление изменения логарифма правдоподобия[math]\Delta LL[/math] имеет сложность [math]O(1)[/math]

Сложность алгоритма на одной итерации:

[math]O(k(d^2+dm+m+m+dm+d^2m+1+d+d^2) = O(d^2mk)[/math], так как мы рассматриваем задачу для двумерного случая, то есть [math]d=2[/math], множитель [math]d^2[/math] можно отнести в константу, итоговая сложность вычисления на одной итерации [math]O(mk)[/math].

Для [math]n[/math] итераций итоговая сложность алгоритма будет равна:

[math]O(mkn)[/math], где [math]m[/math] — число объектов, [math]k[/math] — число кластеров, [math]n[/math] — число итераций.

1.7 Информационный граф

Опишем граф алгоритма для следующих входных данных: [math]m = 3,\; k = 2,\; d = 2[/math], то есть 3 входных объекта и 2 кластера.

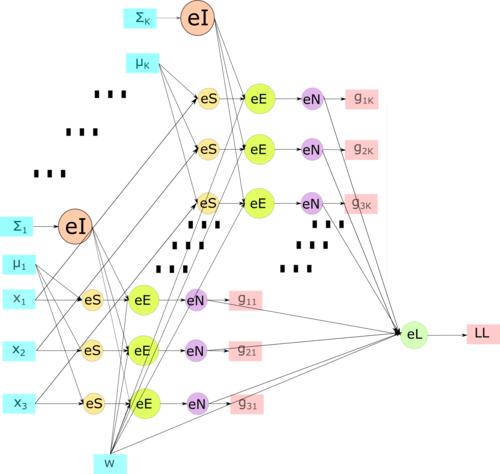
На рис.1 показана макроструктура EM-алгоритма. Входными данными в таком случае являются матрица [math]X \in \R^{3 \times 2}[/math] и число кластеров [math]k = 2[/math]. На шаге [math]\mathbf{init}[/math] происходит инициализация начальных приближений параметров модели и затем итеративное повторение [math]\mathbf{E}[/math] и [math]\mathbf{M}[/math] шагов алгоритма.

Рис.1. Граф EM-алгоритма с отображением входных и выходных данных

E-шаг. На рис.2 детально изображена схема E-шага. Входные параметры [math]x_1,\; x_2,\; x_3 \in \R^{1 \times 2}[/math] являются строчками входной матрицы [math]X[/math], также на вход подаются текущие приближения векторов средних значений ([math]\mu_1, \;\mu_2[/math]), матриц ковариаций ([math]\Sigma_1, \Sigma_2[/math]) и весов [math]w[/math].

Вершинами [math]\mathbf{eI}[/math] обозначена операция нахождения обратной матрицы [math]\Sigma_j^{-1},\; j = 1,2[/math]. Вершины группы [math]\mathbf{eS}[/math] обозначают вычитание векторов [math]x_i - \mu_j,\; i = 1,2,3; \; j = 1, 2[/math]. Салатовые узлы графа [math]\mathbf{eE}[/math] обозначают вычисление ненормированного значения [math]g_{ij}, \;i = 1,2,3;\;j=1,2[/math] по формулам из раздела описания алгоритма. Далее выход вершин этой группы подаётся на вход вершинам [math]\mathbf{eN}[/math], которые обозначают нормировку, затем в [math]\mathbf{eL}[/math] происходит подсчет логарифма правдоподобия. На выходе этого графа получаются скрытые переменные [math]g_{ij}[/math] и логарифм правдоподобия LL.

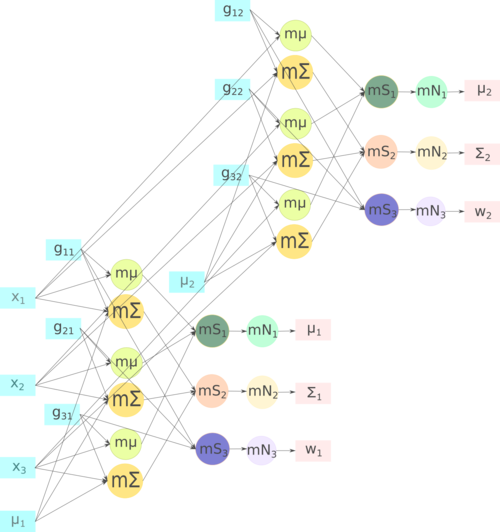
Рис.2. Граф E-шага с отображением входных и выходных данных

M-шаг. На рисунке 3 изображена схема M-шага. Входными параметрами являются: исходные объекты [math]x_1,\; x_2,\; x_3 \in \R^{1 \times 2}[/math], скрытые переменные [math]g_{11},\;g_{21},\;g_{31},\;\mu_1[/math] для пересчета параметров первого кластера и [math]g_{12},\;g_{22},\;g_{32},\;\mu_2[/math] — для второго.

Вершина [math]\mathbf{m}\boldsymbol{\mu}[/math] обозначает подсчет слагаемого математического ожидания для одного объекта, затем на шаге [math]\mathbf{mS_1}[/math] происходит суммирование слагаемых, и, наконец, на шаге [math]\mathbf{mN_1}[/math] нормировка математического ожидания, выходом являются [math]\mu_1,\;\mu_2[/math]. Вершина [math]\mathbf{m}\boldsymbol{\Sigma}[/math] обозначает подсчет слагаемого матрицы ковариации для одного объекта, затем на шаге [math]\mathbf{mS_2}[/math] происходит суммирование слагаемых, и, наконец, на шаге [math]\mathbf{mN_2}[/math] нормировка матрицы ковариации, выходом являются [math]\Sigma_1,\;\Sigma_2[/math]. Операция [math]\mathbf{mS_3}[/math] обозначает вычисление ненормированного веса для одного шага, затем при выполнении [math]\mathbf{mN_3}[/math] происходит нормировка весов, выходом являются [math]w_1,\;w_2[/math].

Рис.3. Граф M-шага с отображением входных и выходных данных

На рис.1 показана структура ЕM-алгоритма для кластеризации, на рис.2 — структура E-шага и на рис.3 — структура M-шага.

1.8 Ресурс параллелизма алгоритма

Как видно из информационного графа, возможно распараллеливание как по кластерам, так и по объектам. Однако, в реальных задачах число кластеров много меньше числа объектов, поэтому распараллеливание по кластерам нецелесообразно.

В данной статье рассматривается вариант распараллеливания по объектам.

1.9 Входные и выходные данные алгоритма

Входные данные: плотная вещественная матрица объекты-признаки [math]X \in \R^{m \times d}[/math], количество кластеров [math]k[/math]

Объём входных данных: [math]m \times d + 1[/math]

Выходные данные: вектор весов [math]w \in \R^{k \times 1}[/math], [math]\;\;k[/math] векторов [math]\mu_j \in \R^{d \times 1}[/math], [math]\;\;k[/math] матриц [math]\Sigma \in \R^{d \times d}[/math]

Объём выходных данных: [math]k \times (d \times d + d + 1)[/math]

Стоит заметить, что модель смеси распеределения полностью восстанавливается по выходным данным, и задача предсказания метки кластера для входных объектов является тривиальной.

1.10 Свойства алгоритма

Соотношение последовательной и параллельной сложности являются константой([math]O(mkn)[/math] к [math]O(mkn)[/math]).

Вычислительная мощность алгоритма равна отношению числа операций к суммарному объему входных и выходных данных. Она показывает, сколько операций приходится на единицу переданных данных. Несмотря на простоту данного понятия, это значение исключительно полезно на практике: чем выше вычислительная мощность, тем меньше накладных расходов вызывает перемещение данных для их обработки, например, на сопроцессоре, ускорителе или другом узле кластера. Например, вычислительная мощность скалярного произведения двух векторов равна всего лишь [math]1[/math], а вычислительная мощность алгоритма умножения двух квадратных матриц равна [math]2n/3[/math].

EM-алгоритм не является устойчивым, результат его работы сильно зависит от начальных приближений параметров. При неудачном выборе начальных приближений алгоритм может не сойтись или сойтись в локальный экстремум.

Алгоритм сбалансирован по E и M шагам, затраты на выполнение этих этапов примерно одинаковы.

Алгоритм не является детерминированным. Здесь предполагается, что инициализация начальных параметров не относится к вычислительной части алгоритма. Причиной недетерминированности являются ошибки округления, которые могут менятся от запуска к запуску. Однако, эти ошибки незначительно влияют на результат работы алгоритма.

Степень исхода вершины информационного графа показывает, в скольких операциях ее результат будет использоваться в качестве аргумента. Если степень исхода вершины велика, то на этапе реализации алгоритма нужно позаботиться об эффективном доступе к результату ее работы. В этом смысле, особый интерес представляют рассылки данных, когда результат выполнения одной операции используется во многих других вершинах графа, причем число таких вершин растет с увеличением значения внешних переменных.

"Длинные" дуги в информационном графе [1] говорят о потенциальных сложностях с размещением данных в иерархии памяти компьютера на этапе выполнения программы. С одной стороны, длина дуги зависит от выбора конкретной системы координат, в которой расположены вершины графа, а потому в другой системе координат они попросту могут исчезнуть (но не появится ли одновременно других длинных дуг?). А с другой стороны, вне зависимости от системы координат их присутствие может быть сигналом о необходимости длительного хранения данных на определенном уровне иерархии, что накладывает дополнительные ограничения на эффективность реализации алгоритма. Одной из причин возникновения длинных дуг являются рассылки скалярных величин по всем итерациям какого-либо цикла: в таком виде длинные дуги не вызывают каких-либо серьезных проблем на практике.

Для проектирования специализированных процессоров или реализации алгоритма на ПЛИС представляют интерес компактные укладки информационного графа [1], которые также имеет смысл привести в данном разделе.

2 ЧАСТЬ. Программная реализация алгоритма

2.1 Особенности реализации последовательного алгоритма

В данном разделе приведем код реализации последовательного алгоритма. 

double_vector em_algo::expectation_step(double_matrix& features)
{
    long n_objects = features.size1();
    int n_clusters = parameters.sigmas.size();
    double pi = boost::math::constants::pi<double>();

    // precalculate inverse matrices and dets
    std::vector<double_matrix> sigmas_inverted(n_clusters);
    std::vector<double> norm_distribution_denominator(n_clusters);
    for (int i = 0; i < n_clusters; ++i)
    {        
        double_matrix sigma_inverted(parameters.sigmas[i].size1(), parameters.sigmas[i].size2());
        double det = InvertMatrix(parameters.sigmas[i], sigma_inverted);
        if (det == 0)
        {
            std::cerr << "Matrix can not be inverted\n";
            exit(1);
        }
        norm_distribution_denominator[i] = sqrt(pow(2 * pi, parameters.n_features) * det);
        sigmas_inverted[i] = sigma_inverted;
    }

    hidden_vars = double_matrix(n_objects, n_clusters);
    double_vector log_likelihood(n_objects, 0);

    for (auto i = 0; i < n_objects; ++i)
    {
        double_matrix_row x(features, i);
        double norm_value = 0;
        for (auto j = 0; j < n_clusters; ++j)
        {
            double_matrix_column current_means(parameters.means, j);
            double_vector x_centered = x - current_means;

            double exp_power = -0.5 * inner_prod(prod(x_centered, sigmas_inverted[j]), x_centered);
            hidden_vars(i, j) = parameters.weights(j) * exp(exp_power) / norm_distribution_denominator[j];

            norm_value += hidden_vars(i, j);
        }
        double_matrix_row hidden_vars_row(hidden_vars, i);
        if (norm_value != 0)
        {
            hidden_vars_row = hidden_vars_row / norm_value;
            log_likelihood(i) = log(inner_prod(hidden_vars_row, parameters.weights));
        }

    }
    return log_likelihood;
}

void em_algo::maximization_step(double_matrix& features)
{
    int n_objects = features.size1();

    double_vector w = double_vector(n_clusters, 0.0);
    double_matrix means = double_matrix(parameters.n_features, n_clusters, 0.0);
    std::vector<double_matrix> sigmas;
    for (int j = 0; j < n_clusters; ++j)
        sigmas.push_back(double_matrix(parameters.n_features, parameters.n_features, 0.0));

    for (int i = 0; i < n_objects; ++i)
    {
        double_matrix_row x_i = row(features, i);

        for (int j = 0; j < n_clusters; ++j)
        {
            double g = hidden_vars(i, j);
            w(j) += g;

            double_matrix_column single_mean = column(means, j);

            single_mean += g * x_i;

            double_vector x_centered = x_i - column(parameters.means, j);
            for (int k = 0; k < parameters.n_features; ++k)
                for (int l = 0; l < parameters.n_features; ++l)
                    sigmas[j](k, l) = sigmas[j](k, l) + g * x_centered(k) * x_centered(l);
        }
    }
    // update weights
    parameters.weights = w / n_objects;

    for (int j = 0; j < n_clusters; ++j) {
        double weight = w(j);
        // update means
        double_matrix_column means_old = column(parameters.means, j);
        double_matrix_column means_new = column(means, j);
        means_old = means_new / weight;

        // update sigmas
        parameters.sigmas[j] = sigmas[j] / weight;
        for (int k = 0; k < parameters.n_features; ++k)
            parameters.sigmas[j](k, k) = parameters.sigmas[j](k, k) + tol;
    }
}

bool em_algo::is_likelihood_stabilized(double_vector likelihood, double_vector previous_likelihood)
{
    double likelihood_diff = sum(likelihood) - sum(previous_likelihood);
    return fabs(likelihood_diff) < tol;
}

model em_algo::process(double_matrix& features, int max_iterations)
{
    int iteration = 0;
    double_vector likelihood, previous_likelihood;
    while (iteration++ < max_iterations && (iteration <= 2 || !is_likelihood_stabilized(likelihood, previous_likelihood)))
    {
        previous_likelihood = likelihood;
        likelihood = expectation_step(features);
        maximization_step(features);
    }
    return parameters;
}

Возможной реализацией является перестановка местами циклов по объектам и по кластерам на E и М шаге. В данном случае внешний цикл проходит по объектам, так как подразумевается дальнейшая реализации распараллеливания по объектам. При реализации только последовательного алгоритма более понятной версией будет реализация внешнего цикла по кластерам, и внутреннего по объектам, но такая реализация увеличит число обращений в память и общее время работы алгоритма.

2.2 Возможные способы и особенности параллельной реализации алгоритма

Раздел довольно обширный, в котором должны быть описаны основные факты и положения, формирующие параллельную программу. К их числу можно отнести:

  • представленный иерархически ресурс параллелизма, опирающийся на структуру циклических конструкций и на граф вызовов программы;
  • комбинацию (иерархию) массового параллелизма и параллелизма конечного;
  • возможные способы распределения операций между процессами/нитями;
  • возможные способы распределения данных;
  • оценку количества операций, объёма и числа пересылок данных (как общего числа, так и в пересчёте на каждый параллельный процесс);

и другие.

В этом же разделе должны быть даны рекомендации или сделаны комментарии относительно реализации алгоритма с помощью различных технологий параллельного программирования: MPI, OpenMP, CUDA или использования директив векторизации.

2.3 Масштабируемость алгоритма и его реализации

Задача данного раздела - показать пределы масштабируемости алгоритма на различных платформах. Очень важный раздел. Нужно выделить, описать и оценить влияние точек барьерной синхронизации, глобальных операций, операций сборки/разборки данных, привести оценки или провести исследование сильной и слабой масштабируемости алгоритма и его реализаций.

Масштабируемость алгоритма определяет свойства самого алгоритма безотносительно конкретных особенностей используемого компьютера. Она показывает, насколько параллельные свойства алгоритма позволяют использовать возможности растущего числа процессорных элементов. Масштабируемость параллельных программ определяется как относительно конкретного компьютера, так и относительно используемой технологии программирования, и в этом случае она показывает, насколько может вырасти реальная производительность данного компьютера на данной программе, записанной с помощью данной технологии программирования, при использовании бóльших вычислительных ресурсов (ядер, процессоров, вычислительных узлов).

Ключевой момент данного раздела заключается в том, чтобы показать реальные параметры масштабируемости программы для данного алгоритма на различных вычислительных платформах в зависимости от числа процессоров и размера задачи [4]. При этом важно подобрать такое соотношение между числом процессоров и размером задачи, чтобы отразить все характерные точки в поведении параллельной программы, в частности, достижение максимальной производительности, а также тонкие эффекты, возникающие, например, из-за блочной структуры алгоритма или иерархии памяти.

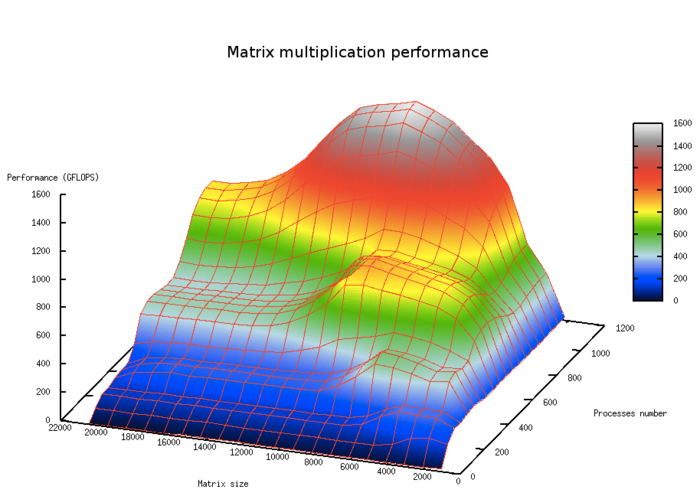
На рис.5. показана масштабируемость классического алгоритма умножения плотных матриц в зависимости от числа процессоров и размера задачи. На графике хорошо видны области с большей производительностью, отвечающие уровням кэш-памяти.

Рис.5 Масштабируемость классического алгоритма умножения плотных матриц в зависимости от числа процессоров и размера задачи

2.4 Динамические характеристики и эффективность реализации алгоритма

Это объемный раздел AlgoWiki, поскольку оценка эффективности реализации алгоритма требует комплексного подхода [5], предполагающего аккуратный анализ всех этапов от архитектуры компьютера до самого алгоритма. Основная задача данного раздела заключается в том, чтобы оценить степень эффективности параллельных программ, реализующих данный алгоритм на различных платформах, в зависимости от числа процессоров и размера задачи. Эффективность в данном разделе понимается широко: это и эффективность распараллеливания программы, это и эффективность реализации программ по отношению к пиковым показателям работы вычислительных систем.

Помимо собственно показателей эффективности, нужно описать и все основные причины, из-за которых эффективность работы параллельной программы на конкретной вычислительной платформе не удается сделать выше. Это не самая простая задача, поскольку на данный момент нет общепринятой методики и соответствующего инструментария, с помощью которых подобный анализ можно было бы провести. Требуется оценить и описать эффективность работы с памятью (особенности профиля взаимодействия программы с памятью), эффективность использования заложенного в алгоритм ресурса параллелизма, эффективность использования коммуникационной сети (особенности коммуникационного профиля), эффективность операций ввода/вывода и т.п. Иногда достаточно интегральных характеристик по работе программы, в некоторых случаях полезно показать данные мониторинга нижнего уровня, например, по загрузке процессора, кэш-промахам, интенсивности использования сети Infiniband и т.п. Хорошее представление о работе параллельной MPI-программы дают данные трассировки, полученные, например, с помощью системы Scalasca.

2.5 Существующие реализации алгоритма

Существуют следующие последовательные реализации EM-алгоритма для кластеризации: opencv, scikit-learn

3 Литература

[1] Воеводин В.В., Воеводин Вл.В. Параллельные вычисления. - СПб.: БХВ-Петербург, 2002. - 608 с.

[2] К.В.Воронцов. Математические методы обучения по прецедентам (теория обучения машин)

Источник — https://algowiki-project.org/w/ru/index.php?title=Участник:Мария_Готман/Алгоритм_кластеризации,_основанный_на_максимизации_ожидания&oldid=5064