Участник:Astandrik/Алгоритм кластеризации, основанный на минимальном остовном дереве

Алгоритм кластеризации, основанный на минимальном остовном дереве
Последовательный алгоритм
Последовательная сложность	-
Объём входных данных	-
Объём выходных данных	-
Параллельный алгоритм
Высота ярусно-параллельной формы	-
Ширина ярусно-параллельной формы	-

Основные авторы описания: Стандрик Антон Сергеевич

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Данный алгоритм предназначен для решения задач кластеризации. Говоря в общем, кластеризация — многомерная статистическая процедура, выполняющая сбор данных, содержащих информацию о выборке объектов, и затем упорядочивающая объекты в сравнительно однородные группы .

Впервые идея использования минимального остовного дерева для кластеризации данных была преждожена C. T. Zah в 1971 году. Этот метод широко используется исследователями при анализе изображений , а также при анализе биологических данных .

В общем описании работы алгоритма можно выделить следующие шаги:

1. Построение минимального остовного дерева по заданному множеству. Этот шаг разбивается на два подшага:
   1. Определение метрики пространства, в котором осуществляется кластерный анализ. В качестве примеров метрик можно привести:
      • Метрика Евклида: [math]d_{ij} = \sqrt{\sum^n_{k=1}(x_{ik} - x_{jk})^2}[/math]
      • Метрика city-block (манхэттенская метрика): [math]d_{ij} = \sum^n_{k=1}|x_{ik} - x_{jk}| [/math]
      • Метрика Брея-Картиса: [math]d_{ij} = \sum^n_{k=1}\frac{|x_{ik} - x_{jk}|}{|x_{ik} + x_{jk}| }[/math]
   2. Выбор алгоритма построения минимального остовного дерева:
      • Алгоритм Прима
      • Алгоритм Крускала
      • Алгоритм Борувки
2. Разделение полученного дерева на несвязное множество поддеревьев в соответствии с некоторой стратегией. Можно выделить три популярные стратегии кластеризации:
   • SEMST (standard Euclidean minimum spanning tree clustering algorithm) - предполагается, что нам заранее известно число кластеров. В таком случае, если число кластеров равно [math]k[/math], то из полученного в первом пункте остовного дерева удаляются [math]k-1[/math] связей с наибольшим весом.
   • CEMST(The maximum cost minimum spanning tree) - Работает так же как и SEMST, однако вместо веса вершины используется её стоимость, которая вычисляется следующим образом: Пусть ребро [math]e = (x_{i}, x_{j})[/math], тогда [math]cost(e) = w(e) * degree(x_{i}) * degree(x_{j})[/math]. Далее, зная число кластеров [math]k[/math] и стоимости рёбер, удаляются [math]k-1[/math] рёбер с максимальной стоимостью.
   • ZEMST (The Zahn’s minimum spanning tree) - от двух предыдущих эта стратегия отличается тем, что здесь число кластеров не известно заранее, а вычисляется в процессе кластеризации. Его суть в том, что удаляются те рёбра, веса которых значительно превосходят средний вес ребра в соседних поддеревьях.

1.1.1 Достоинства

Основным достоинством алгоритма является его способность выделять кластеры произвольной формы.

1.1.2 Недостатки

Недостатком является трудность определения четких критериев, при которых осуществляется разбиение данных на разные кластеры.

Кроме того, существуют наборы данных, на которых популярные алгоритмы (SEMST, CEMST, ZEMST) не дают правильного результата, и для которых требуется применение более сложных алгоритмов (например HEMST с временем работы [math]O(n^2 * log(n))[/math])

Кластеры, соединенные через точку.

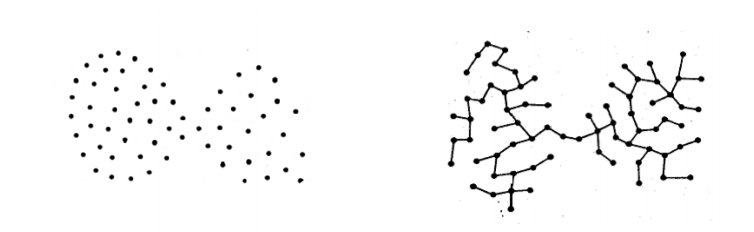
Если взять в качестве примера набор данных, изображенных на рисунке выше, то видно, что простая стратегия "удалять самые длинные связи" здесь не сработает, и потребуется более сложный алгоритм для правильного нахождения кластеров.

1.2 Математическое описание алгоритма

Исходные данные: набор векторов размерности [math]n[/math] : [math](a_1, a_2, ..., a_n)[/math], где [math] a_j \in \mathbb {R} \quad \forall j \in [1,n] [/math].

Вычисляемые данные: Сгруппированные по кластерам данные.

1.2.1 Основные обозначения

• [math]G = (V,E) [/math] - граф, заданный множеством вершин [math]V[/math] и множеством рёбер [math]E[/math]
• [math]E[/math] - множество рёбер графа
• [math]V[/math] - множество вершин графа
• [math]MST(G)[/math] (minimum spanning tree) - минимальное остовное дерево графа [math][/math]. Остовное дерево — ациклический связный подграф данного связного неориентированного графа, в который входят все его вершины. Минимальное остовное дерево в связанном взвешенном неориентированном графе — это остовное дерево этого графа, имеющее минимальный возможный вес, где под весом дерева понимается сумма весов входящих в него рёбер.

1.3 Вычислительное ядро алгоритма

Процесс решения задачи кластеризации при помощи минимального остовного дерева может быть разделен на три независимых этапа:

1. Приведение задачи наборе векторов данных к задаче о поиске минимального остовного дерева в графе (то есть нахождение расстояний между всеми парами данных векторов с использованием выбранной метрики, и запись этого расстояния как веса ребра, соединяющего эти вершины). Последовательная сложность: [math] O(n^2) [/math]
2. Поиск минимального остовного дерева. Последовательная сложность: [math] O(E*log(E)) [/math]
3. Разбиение остовного дерева на кластеры. Последовательная сложность зависит от реализации. (от [math] O(1) [/math] в случае SEMST до [math] O(n^2) [/math] в случае ZEMST).

1.9 Входные и выходные данные алгоритма

В качестве входных данных программе дается множество векторов [math](a_1, a_2, ..., a_n)[/math] размерности [math]n[/math]. Для удобства изучения свойств алгоритма и отображения результатов можно брать массив векторов размерности 2. В этом случае наглядность будет обеспечена естественной возможностью отобразить вектора в плоскости.

Выходными данными программы будет множество, состоящее из сгруппированных по кластерам векторов из входных данных.