Участник:Alexboboshko/Решение начальной задачи Коши для системы ОДУ методом Рунге-Кутта 4-го порядка

РК
Последовательный алгоритм
Последовательная сложность	[math] 4mn [/math]
Объём входных данных	[math] m + 3 [/math]
Объём выходных данных	[math] (m+1)n [/math]
Параллельный алгоритм
Высота ярусно-параллельной формы	?
Ширина ярусно-параллельной формы	?

Основные авторы описания:

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Ме́тоды Ру́нге — Ку́тты — важное семейство численных алгоритмов решения обыкновенных дифференциальных уравнений и их систем. Данные итеративные методы явного и неявного приближённого вычисления были разработаны около 1900 года немецкими математиками К. Рунге и М. В. Куттой.

Формально, методом Рунге — Кутты является модифицированный и исправленный метод Эйлера, они представляют собой схемы второго порядка точности. Существуют стандартные схемы третьего порядка, не получившие широкого распространения.

1.2 Математическое описание алгоритма

1.2.1 Общая формулировка методов

Рассматриваем задачу Коши

[math] \frac{du}{dt} = f(t,u), u(0)=u_0 [/math]

Введем по переменному [math]t[/math] равномерную сетку с шагом [math]\tau \gt 0 [/math], т.е. рассмотрим множество точек

[math] \begin{align} \omega_n = \left \{{t_n = n\tau, \ n = 0,\ 1,\ 2, \ \dots} \right \}. \end{align} [/math]

Будем обозначать через [math]u(t)[/math] точное решение задачи Коши, а через [math] y_n = y(t_n) [/math] - приближенное решение.

Явный m-этапный метод Рунге-Кутта состоит в следующем. Пусть решение [math] y_n = y(t_n) [/math] уже известно. Задаются числовые коэффициенты [math] a_i, \ b_{ij},\ i = 2, 3, \dots, m,\ j = 1, 2, \dots, m-1,\ \sigma_i,\ i = 1, 2, \dots, m, [/math] и последовательно вычисляются функции

[math] \begin{array}{l} k_1 = f(t_n, y_n), \ k_2 = f(t_n+a_2\tau,\ y_n+b_{21}\tau k_1) \\ k_3 = f(t_n+a_3 \tau, \ y_n+b_{31}\tau k_1+b_{32}\tau k_2), \ \dots, \\ k_m = f(t_n+a_m \tau, \ y_n+b_{m1}\tau k_1+b_{m2}\tau k_2+\dots+b_{m,m-1}\tau k_{m-1}) \end{array}{l} [/math]

Затем из формулы [math]\frac{y_{n+1}-y_n}{\tau} = \sum_{i = 1}^{m} \sigma_i k_i [/math] находится новое значение [math] y_{n+1} = y(t_{n+1}) [/math]

1.2.2 Метод Рунге-Кутта четвертого порядка для системы ДУ

Запишем задачу Коши в векторном виде

[math] \frac{d \bar y}{dt} = \bar f(t, \bar y); \ \bar y(t_0) = \bar y_0 = \begin{pmatrix} y_{10}\\ \vdots\\ y_{m0}\\ \end{pmatrix} [/math]

[math] a \leq t \leq b [/math]

Зададим равномерную сетку

[math] t_i = a + ih,\ i = 1,\dots, n,\ h = \frac{b-a}{n} [/math]

Введём обозначения [math]y(x_i) = y_i[/math].

[math] \begin{cases} \bar k_1 = h\bar f(t_i,\bar y_i)\\ \bar k_2 = h\bar f(t_i + h/2,\bar y_i + \bar k_1/2)\\ \bar k_3 = h\bar f(t_i + h/2,\bar y_i + \bar k_2/2)\\ \bar k_4 = h\bar f(t_i + h,\bar y_i + \bar k_3)\\ \bar y_{i+1} = \bar y_i + [ \bar k_1 + 2\bar k_2 + 2\bar k_3 + \bar k_4 ]/6 \\ \end{cases} [/math]

1.3 Вычислительное ядро алгоритма

В описанной выше вычислительной схеме наиболее трудоемкой является операция расчета правых частей ОДУ при вычислении [math]k_i ( i = 1, \dots, 4) , [/math] то есть основное внимание следует уделить распараллеливанию этой операции.

1.4 Макроструктура алгоритма

program rk_iv; var T:Text;

   x,h,a,b,y1, y2, y3, y4,
   k1_1, k1_2, k1_3, k1_4,
   k2_1, k2_2, k2_3, k2_4,
   k3_1, k3_2, k3_3, k3_4,
   k4_1, k4_2, k4_3, k4_4:real;

function F(x, y1, y2, y3, y4: real; n:byte):real; begin

   case n of
   1: f:=-y2;
   2: f:=y1;
   3: f:=y1-y4;
   4: f:=y2+y3;
   end;

end; begin

   assign(T, 'd:\rk_iv.txt');
   rewrite(T);
   a:=0; b:=2*pi; h:=pi/80;
   y1:=1; y2:=0; y3:=0; y4:=0;
   x:=a;
   while x<=b+h do
   begin
      writeln(T, x:10:5, y1:10:5, y2:10:5, y3:10:5, y4:10:5,
      cos(x):10:5, sin(x):10:5, x*cos(x):10:5, x*sin(x):10:5);
      k1_1:=h*f(x, y1, y2, y3, y4, 1);
      k1_2:=h*f(x, y1, y2, y3, y4, 2);
      k1_3:=h*f(x, y1, y2, y3, y4, 3);
      k1_4:=h*f(x, y1, y2, y3, y4, 4);
      k2_1:=h*f(x+h/2, y1+k1_1/2, y2+k1_2/2, y3+k1_3/2, y4+k1_4/2, 1);
      k2_2:=h*f(x+h/2, y1+k1_1/2, y2+k1_2/2, y3+k1_3/2, y4+k1_4/2, 2);
      k2_3:=h*f(x+h/2, y1+k1_1/2, y2+k1_2/2, y3+k1_3/2, y4+k1_4/2, 3);
      k2_4:=h*f(x+h/2, y1+k1_1/2, y2+k1_2/2, y3+k1_3/2, y4+k1_4/2, 4);
      k3_1:=h*f(x+h/2, y1+k2_1/2, y2+k2_2/2, y3+k2_3/2, y4+k2_4/2, 1);
      k3_2:=h*f(x+h/2, y1+k2_1/2, y2+k2_2/2, y3+k2_3/2, y4+k2_4/2, 2);
      k3_3:=h*f(x+h/2, y1+k2_1/2, y2+k2_2/2, y3+k2_3/2, y4+k2_4/2, 3);
      k3_4:=h*f(x+h/2, y1+k2_1/2, y2+k2_2/2, y3+k2_3/2, y4+k2_4/2, 4);
      k4_1:=h*f(x+h,y1+k3_1, y2+k3_2, y3+k3_3, y4+k3_4, 1);
      k4_2:=h*f(x+h,y1+k3_1, y2+k3_2, y3+k3_3, y4+k3_4, 2);
      k4_3:=h*f(x+h,y1+k3_1, y2+k3_2, y3+k3_3, y4+k3_4, 3);
      k4_4:=h*f(x+h,y1+k3_1, y2+k3_2, y3+k3_3, y4+k3_4, 4);
      y1:=y1+1/6*(k1_1+2*k2_1+2*k3_1+k4_1);
      y2:=y2+1/6*(k1_2+2*k2_2+2*k3_2+k4_2);
      y3:=y3+1/6*(k1_3+2*k2_3+2*k3_3+k4_3);
      y4:=y4+1/6*(k1_4+2*k2_4+2*k3_4+k4_4);
      x:=x+h;
   end;
   flush(T); close(T);

end.

1.5 Схема реализации последовательного алгоритма

Для каждого [math]i[/math] последовательно вычисляются функции [math]k_i \ ( i = 1, \dots, 4) [/math]. После этого вычисляется значение [math]y_{i+1}[/math].

1.6 Последовательная сложность алгоритма

На каждой итерации алгоритма требуется 4 обращения к функции [math] \bar f [/math], 11 умножений и 10 сложений.

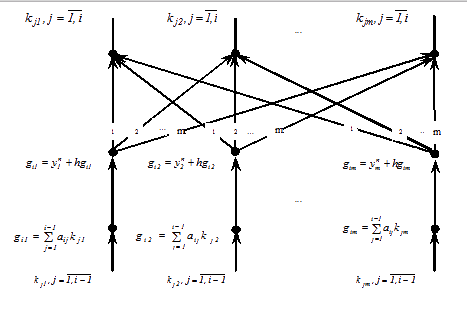
1.7 Информационный граф

1.8 Ресурс параллелизма алгоритма

Поскольку в описанной выше вычислительной схеме наиболее трудоемкой является операция расчета правых частей ОДУ при вычислении [math]k_i ( i = 1, \dots, 4) [/math], то основное внимание следует уделить распараллеливанию этой операции. Здесь будет применяться подход декомпозиции уравнений системы ОДУ на подсистемы. Поэтому для инициализации рассмотрим следующую схему декомпозиции данных по имеющимся процессорным элементам с локальной памятью: на каждый [math]\mu[/math]- ПЭ (процессорный элемент) ([math]\mu = 0, \dots, p-1 [/math]) распределяется [math] m/p [/math] дифференциальных уравнений и вектор [math] \bar y_0 [/math]. Далее расчеты производятся по следующей схеме:

1. на каждом ПЭ одновременно вычисляются [math] m/p [/math] соответствующих компонент вектора [math] \bar k_1 [/math] по формуле [math] [ \bar k_1 ]_{\mu} = h[ \bar f(x_i, \bar y_i) ]_{\mu} [/math]
2. для обеспечения второго расчетного этапа необходимо провести сборку вектора [math] \bar k_1 [/math] целиком на каждом ПЭ. Затем независимо выполняется вычисление компонент вектора [math] \bar k_2 [/math] по формуле [math] [ \bar k_2 ]_{\mu} = h[ \bar f(x_i + h/2,\bar y_i + 1/2 \bar k_1)]_{\mu} [/math];
3. проводится сборка вектора [math] \bar k_2 [/math] на каждом ПЭ, вычисляются компоненты вектора [math] \bar k_3:\ [ \bar k_3 ]_{\mu} = h [\bar f(x_i + h/2,\bar y_i + 1/2 \bar k_2)]_{\mu} [/math];
4. проводится сборка вектора [math] \bar k_3 [/math] на каждом ПЭ, вычисляются компоненты вектора [math] \bar k_4:\ [ \bar k_4 ]_{\mu} = h [\bar f(x_i + h,\bar y_i + \bar k_3)]_{\mu} [/math];
5. рассчитываются с идеальным параллелизмом компоненты вектора [math] \bar y_{i+1}:\ [\bar y_{i+1}]_{\mu} = [\bar y_{i}]_{\mu} + ([ \bar k_1 ]_{\mu} + 2[ \bar k_2 ]_{\mu} + 2[ \bar k_3 ]_{\mu} + [ \bar k_4 ]_{\mu})/6\ [/math] и производится сборка вектора [math] \bar y_{i+1} [/math] на каждом ПЭ. Если необходимо продолжить вычислительный процесс, то полагается [math] i = i + 1 [/math] и осуществляется переход на п. 1

Заметим, что в данном алгоритме производится четыре операции вычисления вектора правых частей ОДУ, шестнадцать операций сложения векторов и умножения вектора на число и четыре операции глобальной сборки векторов.

1.9 Входные и выходные данные алгоритма

Вход:

1. [math] \bar y_{0} \in \mathbb{R}^m [/math] - начальное значение
2. [math]a,\ b[/math] - границы отрезка
3. [math]n[/math] - число итераций

Выход:

1. [math]\bar y_{1},\dots, \bar y_n \in \mathbb{R}^m[/math]
2. [math]\bar x \in \mathbb{R}^n[/math]

1.10 Свойства алгоритма

Методы Рунге-Кутты имеют несколько достоинств, определивших их популярность среди значительного числа исследователей. Эти методы легко программируются. Они обладают достаточными для широкого круга задач свойствами точности и устойчивости. Эти методы (как и все одношаговые методы) являются самостартующими и позволяют на любом этапе вычислений легко изменять шаг интегрирования.

Увеличивая число [math]m[/math] вспомогательных точек, можно построить методы Рунге-Кутты любого порядка точности [math]p[/math]. Однако уже при [math]p\gt 5[/math] эти методы используются довольно редко. Это объясняется как чрезмерной громоздкостью получающихся вычислительных формул, так и том, что преимущества методов высокого порядка точности [math]p[/math] над методами, в которых [math]p=4[/math] и [math]p=5[/math], проявляются либо в тех задачах, где нужна очень высокая точность и используются ЭВМ высокой разрядности, либо в тех задачах, где решение очень гладкое. Кроме того, методы Рунге-Кутты высокого порядка точности часто оказываются менее эффективными по сравнению с методами Адамса того же порядка точности.

Часто используются и более сложные в реализации неявные методы Рунге-Кутты, которые имеют ряд преимуществ перед явными методами, однако это достигается за счет существенного усложнения вычислительного алгоритма, так как на каждом шаге необходимо решать систему нелинейных уравнений.

2 Программная реализация алгоритма

2.7 Существующие реализации алгоритма

Стандартная схема 4-го порядка реализована в различных математических пакетах (Maple, MathCAD, Maxima), в библиотеке для языка программирования Python - SciPy.

3 Литература

[1] Тыртышников Е. Е. Методы численного анализа — М., Академия, 2007.

[2] Бахвалов Н. С., Жидков Н. П., Кобельков. Г. М. — 6-е изд. — М. : БИНОМ. Лаборатория знаний, 2008.

[3] Самарский А. А., Гулин А. В. Численные методы. М.: Наука, 1989. <references \>