Участник:Alexboboshko/Решение начальной задачи Коши для системы ОДУ методом Рунге-Кутта 4-го порядка
| РК | |
| Последовательный алгоритм | |
| Последовательная сложность | [math] 4mn [/math] |
| Объём входных данных | [math] m + 3 [/math] |
| Объём выходных данных | [math] (m+1)n [/math] |
| Параллельный алгоритм | |
| Высота ярусно-параллельной формы | [math] O(n) [/math] |
| Ширина ярусно-параллельной формы | [math] O(m) [/math] |
Авторы: Бобошко А. (1.1, 1.2, 1.7, 1.9, 1.10, 2.4)), Юмакаева А. (1.3, 1.4,1.5, 1.6, 1.8, 2.7)
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Ме́тоды Ру́нге — Ку́тты — важное семейство численных алгоритмов решения обыкновенных дифференциальных уравнений и их систем. Данные итеративные методы явного и неявного приближённого вычисления были разработаны около 1900 года немецкими математиками К. Рунге и М. В. Куттой.
Формально, методом Рунге — Кутты является модифицированный и исправленный метод Эйлера, они представляют собой схемы второго порядка точности. Существуют стандартные схемы третьего порядка, не получившие широкого распространения.
Запишем точную формулу для получения [math]y_{i+1}[/math] :
- [math] y_{i+1} = y_i + \int\limits_{t_i}^{t_{i+1}}f(t,y)dt [/math]
Основная идея алгоритмов Рунге-Кутты состоит в замене функции [math]f(t,y)[/math], которая зависит от неизвестной функции [math]y(t)[/math], некоторым приближением. Чем точнее будет приближенное значение подынтегральной функции, тем точнее будет посчитан интеграл и точнее будет определено значение [math]y_{i+1}[/math].
1.2 Математическое описание алгоритма
1.2.1 Общая формулировка методов
Рассматриваем задачу Коши
- [math] \frac{du}{dt} = f(t,u), u(0)=u_0 [/math]
Введем по переменному [math]t[/math] равномерную сетку с шагом [math]\tau \gt 0 [/math], т.е. рассмотрим множество точек
- [math] \begin{align} \omega_n = \left \{{t_n = n\tau, \ n = 0,\ 1,\ 2, \ \dots} \right \}. \end{align} [/math]
Будем обозначать через [math]u(t)[/math] точное решение задачи Коши, а через [math] y_n = y(t_n) [/math] - приближенное решение.
Явный m-этапный метод Рунге-Кутта состоит в следующем. Пусть решение [math] y_n = y(t_n) [/math] уже известно. Задаются числовые коэффициенты [math] a_i, \ b_{ij},\ i = 2, 3, \dots, m,\ j = 1, 2, \dots, m-1,\ \sigma_i,\ i = 1, 2, \dots, m, [/math] и последовательно вычисляются функции
- [math] \begin{array}{l} k_1 = f(t_n, y_n), \ k_2 = f(t_n+a_2\tau,\ y_n+b_{21}\tau k_1) \\ k_3 = f(t_n+a_3 \tau, \ y_n+b_{31}\tau k_1+b_{32}\tau k_2), \ \dots, \\ k_m = f(t_n+a_m \tau, \ y_n+b_{m1}\tau k_1+b_{m2}\tau k_2+\dots+b_{m,m-1}\tau k_{m-1}) \end{array}{l} [/math]
Затем из формулы [math]\frac{y_{n+1}-y_n}{\tau} = \sum_{i = 1}^{m} \sigma_i k_i [/math] находится новое значение [math] y_{n+1} = y(t_{n+1}) [/math]
1.2.2 Метод Рунге-Кутта четвертого порядка для системы ДУ
Запишем задачу Коши в векторном виде
- [math] \frac{d \bar y}{dt} = \bar f(t, \bar y); \ \bar y(t_0) = \bar y_0 = \begin{pmatrix} y_{10}\\ \vdots\\ y_{m0}\\ \end{pmatrix} [/math]
- [math] a \leq t \leq b [/math]
Зададим равномерную сетку
- [math] t_i = a + ih,\ i = 1,\dots, n,\ h = \frac{b-a}{n} [/math]
Введём обозначения [math]y(x_i) = y_i[/math].
- [math] \begin{cases} \bar k_1 = h\bar f(t_i,\bar y_i)\\ \bar k_2 = h\bar f(t_i + h/2,\bar y_i + \bar k_1/2)\\ \bar k_3 = h\bar f(t_i + h/2,\bar y_i + \bar k_2/2)\\ \bar k_4 = h\bar f(t_i + h,\bar y_i + \bar k_3)\\ \bar y_{i+1} = \bar y_i + [ \bar k_1 + 2\bar k_2 + 2\bar k_3 + \bar k_4 ]/6 \\ \end{cases} [/math]
1.3 Вычислительное ядро алгоритма
В описанной выше вычислительной схеме наиболее трудоемкой является операция расчета правых частей ОДУ при вычислении [math]k_i ( i = 1, \dots, 4) , [/math] то есть основное внимание следует уделить распараллеливанию этой операции.
1.4 Макроструктура алгоритма
Каждая итерация алгоритма может быть представлена следующими этапами:
1. Вычисление коэффициентов [math]k_i , i = 1, \dots, 4 , [/math]
2. Вычисление следующего приближения [math] y_{i+1} = y_i + [k_1 + 2 k_2 + 2 k_3 + k_4 ]/6[/math]
3. Переход на следующую итерацию или выход из цикла
1.5 Схема реализации последовательного алгоритма
Для каждого [math]i[/math] последовательно вычисляются функции [math]k_i \ ( i = 1, \dots, 4) [/math]. После этого вычисляется значение [math]y_{i+1}[/math].
Пример программы на языке C
#include <stdio.h>
void main(){
float t=0, dt = 0.05;
float vx = 1, vy = 2;
float x=0, y=0;
vector U(x, y, vx, vy);
vector k1, k2, k3, k4;
while(U.y >= 0){
k1 = F(U, t)*dt;
k2 = F(U + 0.5*k1, t+0.5*dt)*dt;
k3 = F(U + 0.5*k2, t+0.5*dt)*dt;
k4 = F(U + k3, t+dt)*dt;
U = U + 1/6.0 * (k1 + 2*k2 + 2*k3 + k4);
t += dt;
}
}
1.6 Последовательная сложность алгоритма
На каждой итерации алгоритма требуется 4 обращения к функции [math] \bar f [/math], 11 умножений и 10 сложений. Так как функция [math] \bar f [/math] может быть функцией совершенно различной природы (линейная, полином или производная от элементарных функций и т.д.), то заранее оценить её сложность можно только лишь сверху какой-нибудь константой [math] c [/math]. В таком случае последовательную сложность алгоритма можно считать равной [math] 4mnc [/math], но далее для простоты расчетов примем константу [math] c=1 [/math]
1.7 Информационный граф
p.s. можете, пожалуйста, в обсуждении поточнее указать, что именно нужно исправить в рисунке? спасибо
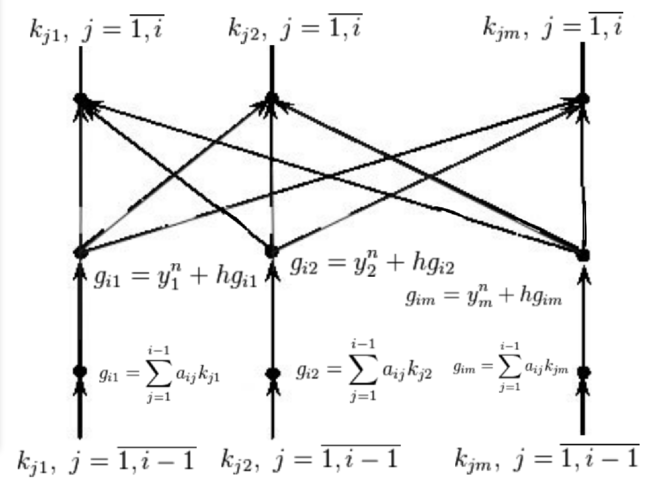
Для системы обыкновенных дифференциальных уравнений размерности [math]m[/math] явный [math]s[/math]-стадийный метод Рунге-Кутты имеет следующий вид: [math] \begin{cases} \bar y_{n+1} = \bar y_n + h\sum\limits^{s}_{i=1} b_{i}k_{i}\\ \bar k_i = \bar f(x_n + c_{i}h; \ \bar g_i); i = \overline{1,s}\\ \bar g_i = \bar y_n + h\sum\limits^{i-1}_{j=1}a_{ij}\bar k_j\\ \end{cases} [/math]
Вычисление любой аппроксимации решения состоит в вычислении множества коэффициентов [math]k_i =(k_i1,k_i2,...,k_im), i=\overline{1,s}[/math] и,собственно,приближенного решения [math]y_{n+1}(h)[/math].Для явных схем вычисление шаговых коэффициентов есть сугубо последовательный процесс. Для разработки параллельного алгоритма использовался математический аппарат графов влияния [1].
Задача распараллеливания в такой постановке сводится к отысканию максимального независимого множества вершин орграфа, причем вершинам графа сопоставляются выполняемые операции и вершины соединяются дугами тогда и только тогда, когда результат выполнения одной операции влияет на результат смежной. На рисунке выше приведен граф влияния для вычисления вектора значений [math]i[/math]-го шагового коэффициента в случае, если [math]m=p[/math].
В общем случае для каждого шагового коэффициента [math]k_i , i = \overline{1, s}[/math] , соответственно, [math]l[/math] компонент вектора [math]g_i , i = \overline{1, s}[/math] могут быть вычислены параллельно
1) [math]l=m[/math] компонент при [math]m=p[/math];
2) [math]l=[m/p][/math] компонент при [math]m\gt p[/math].
1.8 Ресурс параллелизма алгоритма
Поскольку в описанной выше вычислительной схеме наиболее трудоемкой является операция расчета правых частей ОДУ при вычислении [math]k_i ( i = 1, \dots, 4) [/math], то основное внимание следует уделить распараллеливанию этой операции. Здесь будет применяться подход декомпозиции уравнений системы ОДУ на подсистемы. Поэтому для инициализации рассмотрим следующую схему декомпозиции данных по имеющимся процессорным элементам с локальной памятью: на каждый [math]\mu[/math]- ПЭ (процессорный элемент) ([math]\mu = 0, \dots, p-1 [/math]) распределяется [math] m/p [/math] дифференциальных уравнений и вектор [math] \bar y_0 [/math]. Далее расчеты производятся по следующей схеме:
- на каждом ПЭ одновременно вычисляются [math] m/p [/math] соответствующих компонент вектора [math] \bar k_1 [/math] по формуле [math] [ \bar k_1 ]_{\mu} = h[ \bar f(x_i, \bar y_i) ]_{\mu} [/math]
- для обеспечения второго расчетного этапа необходимо провести сборку вектора [math] \bar k_1 [/math] целиком на каждом ПЭ. Затем независимо выполняется вычисление компонент вектора [math] \bar k_2 [/math] по формуле [math] [ \bar k_2 ]_{\mu} = h[ \bar f(x_i + h/2,\bar y_i + 1/2 \bar k_1)]_{\mu} [/math];
- проводится сборка вектора [math] \bar k_2 [/math] на каждом ПЭ, вычисляются компоненты вектора [math] \bar k_3:\ [ \bar k_3 ]_{\mu} = h [\bar f(x_i + h/2,\bar y_i + 1/2 \bar k_2)]_{\mu} [/math];
- проводится сборка вектора [math] \bar k_3 [/math] на каждом ПЭ, вычисляются компоненты вектора [math] \bar k_4:\ [ \bar k_4 ]_{\mu} = h [\bar f(x_i + h,\bar y_i + \bar k_3)]_{\mu} [/math];
- рассчитываются с идеальным параллелизмом компоненты вектора [math] \bar y_{i+1}:\ [\bar y_{i+1}]_{\mu} = [\bar y_{i}]_{\mu} + ([ \bar k_1 ]_{\mu} + 2[ \bar k_2 ]_{\mu} + 2[ \bar k_3 ]_{\mu} + [ \bar k_4 ]_{\mu})/6\ [/math] и производится сборка вектора [math] \bar y_{i+1} [/math] на каждом ПЭ. Если необходимо продолжить вычислительный процесс, то полагается [math] i = i + 1 [/math] и осуществляется переход на п. 1
Заметим, что в данном алгоритме производится четыре операции вычисления вектора правых частей ОДУ, шестнадцать операций сложения векторов и умножения вектора на число и четыре операции глобальной сборки векторов. Т.к. количество итераций цикла равно [math] n [/math], а число уравнений равно [math] m [/math], то при классификации по высоте ЯПФ метод относится к алгоритмам со сложностью [math] O(n) [/math] , а при классификации по ширине ЯПФ - к алгоритмам со сложностью [math] O(m)[/math].
1.9 Входные и выходные данные алгоритма
Вход:
- [math] \bar y_{0} \in \mathbb{R}^m [/math] - начальное значение - размерность [math]m[/math]
- [math]a,\ b[/math] - границы отрезка - размерность 2
- [math]n[/math] - число итераций - размерность 1
Итоговый объем входных данных - [math]m+3[/math]
Выход:
- [math]\bar y_{1},\dots, \bar y_n \in \mathbb{R}^m[/math] - [math]n[/math] [math]m[/math]-мерных векторов - размерность [math]nm[/math]
- [math]\bar x \in \mathbb{R}^n[/math] - размерность [math]n[/math]
Итоговый объем выходных данных - [math]n(m+1)[/math]
1.10 Свойства алгоритма
Методы Рунге-Кутты имеют несколько достоинств, определивших их популярность среди значительного числа исследователей.
- Гибкость. Эти методы легко программируются. Также (как и все одношаговые методы) являются самостартующими и позволяют на любом этапе вычислений легко изменять шаг интегрирования.
- Точность и сходимость. Если метод Рунге-Кутта аппроксимирует исходное уравнение, то он сходится при диаметре разбиения [math]h[/math] → 0, причем порядок точности совпадает с порядком аппроксимации. В случае методов 4-го порядка это значит, что ошибка на одном шаге имеет порядок [math]O(h^5)[/math], а суммарная ошибка на конечном интервале интегрирования имеет порядок [math]O(h^4)[/math] .
- Вычислительная мощность алгоритма стремится к константе, так как число операций равно [math]4mn[/math], а суммарный объем входных и выходных данных составляет [math]mn + n + m + 3[/math].
- Устойчивость. Алгоритм устойчив на любом конечном отрезке при условии ограниченности производной [math] \bar f'_y [/math].
Увеличивая число [math]m[/math] вспомогательных точек, можно построить методы Рунге-Кутты любого порядка точности [math]p[/math]. Однако уже при [math]p\gt 5[/math] эти методы используются довольно редко. Это объясняется как чрезмерной громоздкостью получающихся вычислительных формул, так и том, что преимущества методов высокого порядка точности [math]p[/math] над методами, в которых [math]p=4[/math] и [math]p=5[/math], проявляются либо в тех задачах, где нужна очень высокая точность и используются ЭВМ высокой разрядности, либо в тех задачах, где решение очень гладкое. Кроме того, методы Рунге-Кутты высокого порядка точности часто оказываются менее эффективными по сравнению с методами Адамса того же порядка точности.
Часто используются и более сложные в реализации неявные методы Рунге-Кутты, которые имеют ряд преимуществ перед явными методами, однако это достигается за счет существенного усложнения вычислительного алгоритма, так как на каждом шаге необходимо решать систему нелинейных уравнений.
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.2.1 Локальность реализации алгоритма
2.2.1.1 Структура обращений в память и качественная оценка локальности
2.2.1.2 Количественная оценка локальности
2.2.1.3 Анализ на основе теста Apex-Map
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
2.4.1 Масштабируемость алгоритма
2.4.2 Масштабируемость реализации алгоритма
Проведём исследование масштабируемости параллельной реализации согласно методике. Исследование проводилось на суперкомпьютере "Ломоносов" Суперкомпьютерного комплекса Московского университета. Компилятор mpicc, без опций запуска, подключались библиотеки intel/13.1.0 impi/4.1.0 slurm/2.5.6
Минимальная эффективность: 0.0003169 % Максимальная эффективность: 0.8591 %
Оценка масштабируемости по направлению увеличения числа процессоров: -0.0000463530943148
Оценка масштабируемости по по направлению увеличения размерности задачи: -0.00000914692634229
Общая оценка масштабируемости по направлению увеличения параметров : -0.00000347135643949
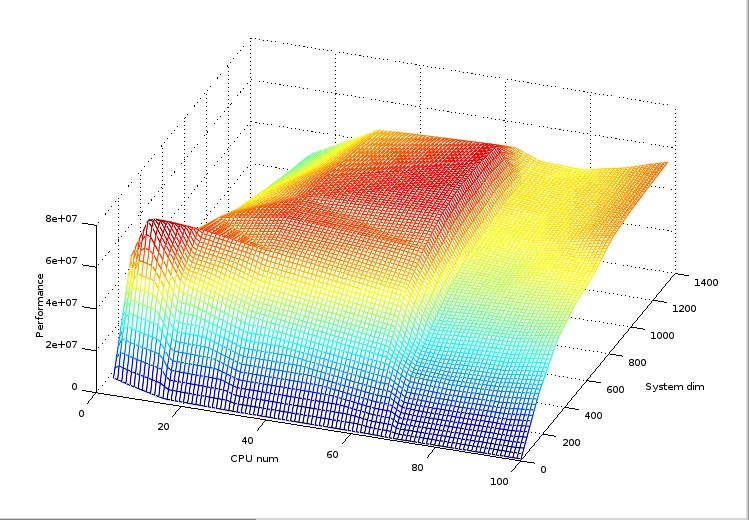
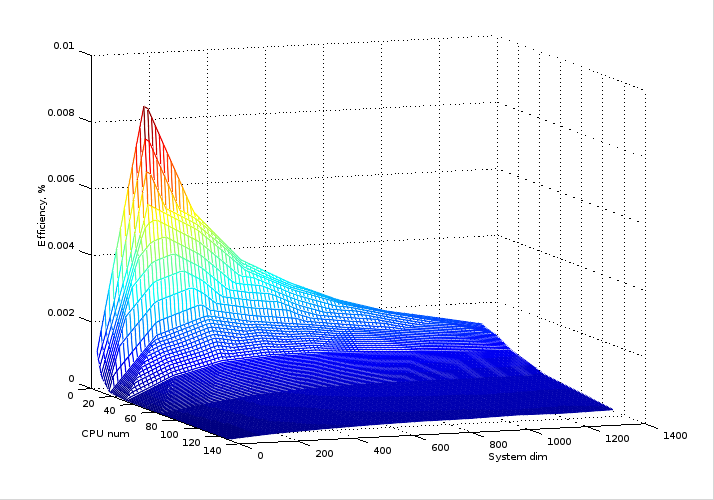
На следующих рисунках представлены графики производительности и эффективности выбранной реализации алгоритма Рунге-Кутта в зависимости от числа процессоров и размерности системы.
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
Стандартная схема 4-го порядка реализована в различных математических пакетах (Maple, MathCAD, Maxima), в библиотеке для языка программирования Python - SciPу, а так же в библиотеке PETSc.
3 Литература
[1] Воеводин В.В., Воеводин Вл. В. Параллельные вычисления. – СПб.: БХВ - Петербург, 2002.
[2] Тыртышников Е. Е. Методы численного анализа — М., Академия, 2007.
[3] Бахвалов Н. С., Жидков Н. П., Кобельков. Г. М. — 6-е изд. — М. : БИНОМ. Лаборатория знаний, 2008.
[4] Самарский А. А., Гулин А. В. Численные методы. М.: Наука, 1989.
[5] Амосов А.А., Дубинский Ю.А., Копченова Н.В. Вычислительные методы для инженеров: Учеб. пособие. — М.: Высш. шк., 1994. <references \>