Участник:Astandrik/Алгоритм кластеризации, основанный на минимальном остовном дереве

Алгоритм кластеризации, основанный на минимальном остовном дереве
Последовательный алгоритм
Последовательная сложность	[math] O(N^2 log(N)) [/math]
Объём входных данных	[math] N [/math]
Объём выходных данных	[math] O(N) [/math]
Параллельный алгоритм
Высота ярусно-параллельной формы	[math] O(log(N)) [/math]
Ширина ярусно-параллельной формы	[math] O(N) [/math]

Основные авторы описания: Стандрик Антон Сергеевич

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Данный алгоритм предназначен для решения задач кластеризации. Говоря в общем, кластеризация — многомерная статистическая процедура, выполняющая сбор данных, содержащих информацию о выборке объектов, и затем упорядочивающая объекты в сравнительно однородные группы .

Впервые идея использования минимального остовного дерева для кластеризации данных была преждожена C. T. Zah в 1971 году. Этот метод широко используется исследователями при анализе изображений , а также при анализе биологических данных .

В общем описании работы алгоритма можно выделить следующие шаги:

1. Разбиение входных векторов на пары и вычисление расстояний в них. Для этого небходим выбор метрики пространства, в котором осуществляется кластерный анализ. В качестве примеров метрик можно привести:
   • Метрика Евклида: [math]d_{ij} = \sqrt{\sum^n_{k=1}(x_{ik} - x_{jk})^2}[/math]
   • Метрика city-block (манхэттенская метрика): [math]d_{ij} = \sum^n_{k=1}|x_{ik} - x_{jk}| [/math]
   • Метрика Брея-Картиса: [math]d_{ij} = \sum^n_{k=1}\frac{|x_{ik} - x_{jk}|}{|x_{ik} + x_{jk}| }[/math]
2. Построение минимального остовного дерева по заданному множеству. Существует три основных алгоритма построения минимального остовного дерева:
   • Алгоритм Прима
   • Алгоритм Крускала
   • Алгоритм Борувки
3. Разделение полученного дерева на несвязное множество поддеревьев в соответствии с некоторой стратегией. Можно выделить три популярные стратегии кластеризации:
   • SEMST (standard Euclidean minimum spanning tree clustering algorithm) - предполагается, что нам заранее известно число кластеров. В таком случае, если число кластеров равно [math]k[/math], то из полученного в первом пункте остовного дерева удаляются [math]k-1[/math] связей с наибольшим весом.
   • CEMST(The maximum cost minimum spanning tree) - Работает так же как и SEMST, однако вместо веса вершины используется её стоимость, которая вычисляется следующим образом: Пусть ребро [math]e = (x_{i}, x_{j})[/math], тогда [math]cost(e) = w(e) * degree(x_{i}) * degree(x_{j})[/math]. Далее, зная число кластеров [math]k[/math] и стоимости рёбер, удаляются [math]k-1[/math] рёбер с максимальной стоимостью.
   • ZEMST (The Zahn’s minimum spanning tree) - от двух предыдущих эта стратегия отличается тем, что здесь число кластеров не известно заранее, а вычисляется в процессе кластеризации. Его суть в том, что удаляются те рёбра, веса которых значительно превосходят средний вес ребра в соседних поддеревьях.

1.1.1 Достоинства

Основным достоинством алгоритма является его способность выделять кластеры произвольной формы. На следующем примере можно видеть, как алгоритм даже в случае SEMST алгоритма корректно разбивает вложенные окружности на три кластера:

Слева направо: Рисунок 1: Начальные данные. Рисунок 2: построенное минимальное остовное дерево. Рисунок 3: разбиение на кластеры путём удаления самых длинных связей.

1.1.2 Недостатки

Недостатком является трудность определения четких критериев, при которых осуществляется разбиение данных на разные кластеры.

Кроме того, существуют наборы данных, на которых популярные алгоритмы (SEMST, CEMST, ZEMST) не дают правильного результата, и для которых требуется применение более сложных алгоритмов (например HEMST с временем работы [math]O(n^2 * log(n))[/math])

В качестве иллюстрации можно привести два похожих визуально, но различных с точки зрения разбиения на кластеры с помощью описываемого алгоритма, примера. (В приведенных примерах первый рисунок обозначает начальный набор данных. Второй - построенное на основе данных минимальное остовное дерево. Третий рисунок - разбиение на кластеры.):

Правильное разбиение на два кластера.

Неверное разбиение на один кластер.

Отличие второго примера - в наличии плотной цепочки связей между двумя кластерами, которая и приводит к ошибке наивного алгоритма удаления самых длинных связей, и таким образом здесь потребуется более сложный алгоритм с более значительным временем работы для правильного нахождения кластеров.

1.2 Математическое описание алгоритма

Исходные данные: набор векторов размерности [math]n[/math] : [math](a_1, a_2, ..., a_n)[/math], где [math] a_j \in \mathbb {R} \quad \forall j \in [1,n] [/math].

Вычисляемые данные: Сгруппированные по кластерам данные.

1.2.1 Основные обозначения

• [math]E[/math] - множество рёбер.
• [math]V[/math] - множество вершин.
• [math]G = (V,E) [/math] - неориентированный граф, заданный множеством вершин [math]V[/math] и множеством рёбер [math]E[/math]
• [math]MST(G)[/math] (Minimum Spanning Tree) - минимальное остовное дерево графа [math][/math]. Остовное дерево — ациклический связный подграф данного связного неориентированного графа, в который входят все его вершины. Минимальное остовное дерево в связанном взвешенном неориентированном графе — это остовное дерево этого графа, имеющее минимальный возможный вес, где под весом дерева понимается сумма весов входящих в него рёбер.
• [math]MSF(G)[/math] (Minimum Spanning Forest) - набор минимальных остовных деревьев для всех компонент связности графа [math] G [/math]

В описании алгоритмов этой статьи часто используется термин "построение MST", подразумевая, что на самом деле в результате построения может получиться как связный, так и несвязный набор деревьев.

1.2.2 Алгоритмы кластеризации

SEMST(standard Euclidean minimum spanning tree) - простейший алгоритм, основанный на заранее известном числе кластеров [math] k [/math]. Путём удаления [math] k - 1 [/math] связей с наибольшим весом предполагается разбиение остовного дерева на нужное количество кластеров. Иными словами минимальное остовное дерево разбивается на [math] k [/math] поддеревьев: [math] G = \{G_1,G_2,...,G_k\} [/math] путём минимизации суммы всех весов: [math] W = \sum ^k_{l=1} \sum _{x_i,x_j \in V_l} w_{x_i,x_j} -\gt min [/math], где [math] V_l [/math] - множество вершин в поддереве [math] G_l [/math]. В конце такой процедуры каждое множество [math] V_l [/math] становится кластером [math] C_l [/math]. Поскольку (в случае использования алгоритма Крускала для построения остовного дерева) рёбра перед началом кластеризации уже отсортированы, для удаления наибольших [math] k [/math] рёбер требуется [math] O(k) [/math] операций, и для распределения получившихся вершин по кластерам требуется время [math] O(n) [/math].

CEMST(maximum cost Euclidean minimum spanning tree) - Работает в точности, как и SEMST, но здесь вместо весов рёбер используется т.н. "стоимость", которая высчитывается следующим образом: если ребро [math] (x_i, x_j) [/math] соединяет вершины [math] x_i [/math] и [math] x_j [/math], то его "стоимость" считается как: [math] Cost_{x_i, x_j} = w_{x_i,x_j} * Deg(x_i) * Deg(x_j) [/math], где [math] Deg(x_i) [/math] - степень вершины [math] x_i [/math] (т.е. количество рёбер графа G, инцидентных вершине [math] x_i [/math]). В остальном алгоритм действует точно так же, как и SEMST, удаляя [math] k-1 [/math] рёбер с наибольшей "стоимостью". Сложность аналогичная. Алгоритм направлен на удаление рёбер, соединяющих высоко нагруженные (с точки зрения количества инцидентных рёбер) вершины.

ZEMST (The Zahn’s maximum spanning tree (Zahn, 1971)) - отличается от двух предыдущих алгоритмов в первую очередь тем, что здесь количество кластеров заранее не известно, но определяется исходя из данных. Данный алгоритм не является жадным, в отличие от первых двух, так как в нём рассматривается не только само ребро и его вес, а также и поддеревья, которые соединены этим ребром. То есть для ребра [math] (x_i, x_j) [/math] рассматриваются поддеревья [math] N_i = (V_{N_i}, E_{N_i}), N_j = (V_{N_j}, E_{N_j}) [/math], где [math] N_i [/math] - поддерево глубины(высоты) [math] d [/math](величина d определяется эмпирически), состоящее из всех достижимых из вершины [math] x_j [/math] вершин за [math] d [/math] шагов через все достижимые из неё рёбра (исключая само ребро [math] (x_i, x_j) [/math]). Введём обозначения:

• [math]\overline{w_{N_i}} = \frac{\sum_{(x_r, x_s) \in E_{N_j}}w_{x_r,x_s}}{|E_{N_j}|} [/math] - средний вес ребра в поддереве [math] N_i [/math]
• [math]\sigma_{N_i} = \frac{\sum_{(x_r, x_s) \in E_{N_j}}\sqrt{(w_{x_r,x_s} - \overline{w_{N_i}})}}{|E_{N_j}|} [/math] - стандартное отклонение веса ребра в поддереве [math] N_i [/math]

Ребро [math] (x_i, x_j) [/math] удаляется из списка в случае, если выполняется хотя бы одно из двух условий:

1. [math] w_{x_i,x_j} \gt \overline{w_{N_i}} - \sigma_{N_i} [/math]
2. [math] w_{x_i,x_j} \gt \overline{w_{N_j}} - \sigma_{N_j} [/math]
3. [math] w_{x_i,x_j} \gt \frac{\sum_{(x_r, x_s) \in E_i \cup E_j}w_{x_r,x_s}}{|E_i \cup E_j|} [/math]

Сложность этого алгоритма составляет в худшем случае [math] O(N^2) [/math] (поскольку может оказаться нужным перебрать все рёбра), а в лушем [math] O(Nd) [/math].

1.3 Вычислительное ядро алгоритма

Процесс решения задачи кластеризации при помощи минимального остовного дерева может быть разделен на три независимых этапа:

1. Приведение задачи наборе векторов данных к задаче о поиске минимального остовного дерева в графе (то есть нахождение расстояний между всеми парами данных векторов с использованием выбранной метрики, и запись этого расстояния как веса ребра, соединяющего эти вершины). Последовательная сложность: [math] O(n^2) [/math]
2. Поиск минимального остовного дерева. Последовательная сложность: [math] O(E*log(E)) [/math]
3. Разбиение остовного дерева на кластеры. Последовательная сложность зависит от реализации. (от [math] O(1) [/math] в случае SEMST до [math] O(n^2) [/math] в случае ZEMST).

1.4 Макроструктура алгоритма

В реализации алгоритма используются следующие структуры данных:

1. Узел(Node)(Вершина) - Представляется набором координат в выбранном пространстве.
2. Ребро(Edge) - Представляется: двумя индексами вершин, которые соединяет; своим весом; флагом, который указывает, входит ли данное ребро в минимальное остовное дерево.

В дальнейшем описании алгоритма используются следующие макрооперации:

1. Вычисление расстояния между вершинами.
2. Добавление ребра в граф - Осуществляется путём выставление специального флага у соответствующего ребра в true;
3. Удаление ребра из графа - Операция, обратная к добавление: соответствующий флаг устанавливается в false. В начальный момент времени у всех рёбер флаг установлен в false, что означает отсутствие рёбер в графе.

Следующие три используемые операции относятся к реализации алгоритма Крускала при помощи леса непересекающихся множеств. Подробнее об этой структуре и связанных операциях можно почитать, например, здесь , в данном пункте они будут только перечислены:

1. Создание дерева с одним узлом - Make-Set
2. Объединение компонент связности - Union
3. Поиск компонент связности - Find-Set

1.5 Схема реализации последовательного алгоритма

int N;        // Размер входных данных
int number_of_clusters;        // Число кластеров
int size = N* (N-1) / 2;        // Количество связей в полном графе
Node nodes[N];        // Вершины(точки), заданные начальными условиями
Edge edges[size];        // Все расстояния между вершинами 
vector<Edge> MST;        // Рёбра минимального остовного дерева
read_data(&nodes, file_name);        // Считывание начальных данных

//----------------Часть 1--------------//
for(int i = 0; i < N-1; i++) {
  for(int j = i+1; j < N; j++) {
	double distance = getDistance(node[i], node[j]);        // Вычисление расстояния между вершинами
	edges[i*N + j] = Edge(i,j,distance);        // Запись значения расстояния в массив
  }
}


//----------------Часть 2--------------//
sort(edges, size);        // Сортировка рёбер графа в порядке возрастания
for(int i = 0; i < size; i++) {        // Обходим список рёбер по возрастанию 
	if(find_set(edges[i].first) != find_set(edges[i].second)) {        // Если вершины принадлежат разным подграфам - связываем их
          Union(edges[i].first, edges[i].second);        // Если вершины принадлежат разным подграфам - связываем их
	  MST.push_back(edges[i]);        // Запись использованного ребра в минимальное остовное дерево
	  edges[i]->is_in_MST = true;     // Запись использованного ребра в минимальное остовное дерево
	}
}


//----------------Часть 3--------------//
for(int i = MST.size() - 1; i > MST.size() - 1 - number_of_clusters; i--) {
	remove_edge(MST, i);        // Удаление самых длинных рёбер из MST - формирование кластеров
}
write_data(MST);        // Запись выходных данных

Как описано в пункте 1.3, весь описываемый алгоритм (начиная от момента получения данных и заканчивая моментом, когда данные отданы на вывод), может быть условно разделён на три части. В то время как первая часть может быть достаточно эффективно решена "в лоб", вторая и третьи части, как указано в пункте 1.1, могут иметь альтернативы. В данном фрагменте кода подробно описано использование Алгоритма Крускала для построения MST, и алгоритма SEMST для разбиения на кластеры.

1.6 Последовательная сложность алгоритма

Как и в остальных пунктах, здесь сложность алгоритма состоит их суммы сложностей трёх его составных частей. Если оценивать сложность асимптотически в зависимости от входных данных, то:

[math] T(n) = O(n^2) + O(\frac{n (n-1)}{2} log(\frac{n (n-1)}{2})) + O(1) [/math]

На первый взгляд второе слагаемое может показаться слишком большим. Однако, верны и следующие равенства:

[math] O(\frac{n (n-1)}{2} log(\frac{n (n-1)}{2}) = O(n^2 log(n^2)) = O(2 n^2 log(n)) = O(n^2 log(n)) [/math]

Отсюда видно, что для входных данных этого алгоритма асимптотические сложности алгоритмов Крускала, Прима и Борувки совпадают.

Таким образом, последовательная сложность алгоритма: [math] O(n^2 log(n)) [/math]

1.7 Информационный граф

Макро-описание параллельного алгоритма кластеризации

1.8 Ресурс параллелизма алгоритма

Данная задача хорошо распараллеливается благодаря тому, что все "тяжелые" вычислительные задачи, начиная с момента считывания входных данных, можно распределить по процессам практически равномерно. Это достигается за счет следующей реализации:

1. Мастер-процесс считывает входные данные и отправляет их остальным процессам с помощью MPI_Broadcast.
2. Все пары точек разбиваются так, что каждому процессу достается одинаковое количество пар.
3. Каждый процесс-рабочий строит MST на своём наборе пар точек.
4. Процессы объединяют свои деревья по алгоритму, изображенному в информационном графе. То есть объединение осуществляется сначала между группами размера [math]2^k[/math], где [math] k \in 1,2,..log_2p[/math], где p - число процессов.

Узким местом в данной параллельной реализации является правильный выбор количества процессов. Для удобства анализа рассматривается число процессоров [math] p = 2^i [/math], где [math] i \in \mathbb {N} [/math]. Ясно, что такое допущение не повлияет на качество анализа, так как другое число процессоров лишь приведет к незначительным накладным расходам, сложность которых асимптотически стремится к нулю. В таком случае можно также ввести допущение о размере входных данных: [math] N = 2^j [/math], где [math] j \in \mathbb {N}, j \gt i [/math]. В этом случае MST-часть дерева графа алгоритма является идеально сбалансированным бинарным деревом. Тогда сложность можно оценить следующим образом:

1. На первом этапе каждый процесс производит расчет на [math] 2^{j - i} * (2^j - 1)[/math] рёбрах, получая локальное MST(или MSF) на не более чем [math] N [/math] вершинах.
2. Далее следует [math] i = log_2(2^i) [/math] шагов объединения не более чем по N рёбер в каждом.

Таким образом, задача эффективного запуска алгоритма состоит в том, чтобы найти оптимальный баланс между количеством расчетов на каждом узле на первом шаге и общим количеством объединений поддеревьев. Пусть дано [math] p = 2^i [/math] вычислительных узлов и [math] N = 2^j [/math]. В таком случае каждый узел получает считает [math] 2^{j - i} * (2^j - 1)[/math] рёбер на первом шаге. Высота части ЯП-формы, отвечающей за MST, равна [math] i [/math]. Тогда всего будет [math] i [/math] уровней объединений MST с числом рёбер не более чем [math] 2N [/math] для каждого вычислительного узла.

Грубая оценка времени вычисления может помочь изучить качественные характеристики алгоритма. Учитывая рассуждения выше, приближенная качественная формула может быть записана таким образом:

• [math] N*logN * p + \frac{N(N - 1)}{2 p} * logN [/math].

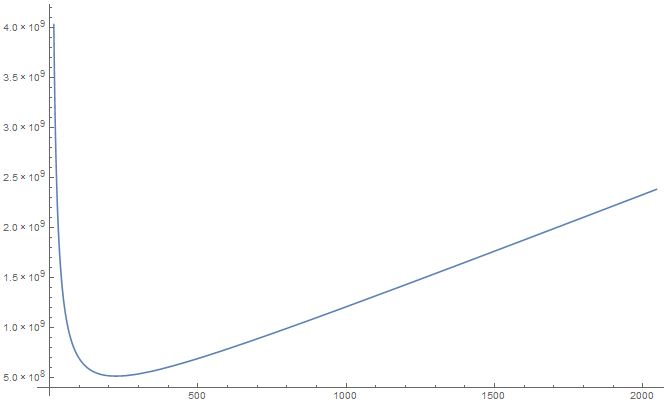
С помощью этой формулы можно построить графики зависимости времени вычислений от количества процессоров и входных данных. Проведём два вычислительных эксперимента:

1. [math] N = 10^5[/math]

По оси абсцисс: количество вычислительных узлов. По оси ординат: время вычислений. При фиксированном [math] N [/math]

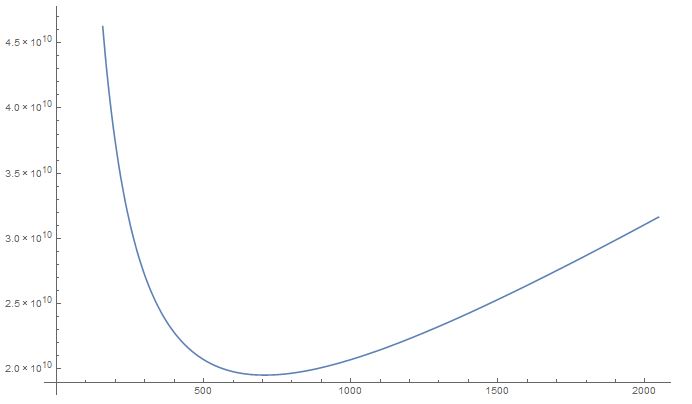
2. [math] N = 10^6 [/math]

По оси абсцисс: количество вычислительных узлов. По оси ординат: время вычислений. При фиксированном [math] N [/math]

Из этих графиков становится видно качественное поведение времени вычислений при увеличении числа процессоров. Можно заметить, что для каждого набора входных данных есть точка, минимизирующая время вычислений. Но в то же время видно, что при слишком большом количестве процессоров алгоритм начинает работать хуже, чем при меньшем. Это вполне понятно: Слишком большое число процессоров порождает большое число обменов между ними, объединений деревьев, сортировок, и т.д. Таким образом именна эта линейная часть [math] N*logN * p [/math] оценки времени вычислений отвечает за ухудшение эффективности алгоритма при числе процессоров, которое больше оптимального. Кроме того, видно, что при увеличении объёма входных данных оптимальное количество процессоров также увеличивается: количество обменов и слияний деревьев компенсируется уменьшением вычислительной нагрузки на каждый отдельный процессор.

1.9 Входные и выходные данные алгоритма

1.9.1 Входные данные

В качестве входных данных программе дается множество векторов [math] x_j = (a_{1j}, a_{2j}, ..., a_{nj})[/math] размерности [math]n[/math]. Для удобства изучения свойств алгоритма и отображения результатов можно брать массив векторов размерности 2. В этом случае наглядность будет обеспечена естественной возможностью отобразить вектора в плоскости.

Кроме того может оказаться полезным особым образом подготовить данные перед анализом (удаление "шумов", выбросов и масштабирование данных по тем или иным координатам).

1.9.2 Выходные данные

Выходными данными программы будет множество [math] M = ((x_1,x_2,..,x_k),(x_{k+1},...),...) [/math], состоящее из сгруппированных по кластерам векторов из входных данных.